added a section grading and bigrading to motivic cohomology where I try to say precisely what the Tate sphere is and precisely what the bigrading is.
I think I know what i am doing (following the cited references) but some expert should eventually check that I got the conventions right and everything.
Concerning my query box at cohomology in the section on bigrading, where I propose that one should look at 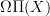 as that gives something that is generated from categorical and geometric speheres:
as that gives something that is generated from categorical and geometric speheres:
maybe that's precisely what captures the passage to the Tate sphere 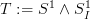 , i.e. the smasch product of both spheres. Both spheres at once.
, i.e. the smasch product of both spheres. Both spheres at once.
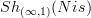 . That's not quite precise: the point is -- as explained in the references linked to there -- that one stabilizes not with respect to the "categorical" or "simplicial" sphere, but with respect to the "geometric" sphere, the
. That's not quite precise: the point is -- as explained in the references linked to there -- that one stabilizes not with respect to the "categorical" or "simplicial" sphere, but with respect to the "geometric" sphere, the 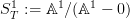 . I have added remarks about this now, but just ever so briefly. Needs to be expanded on later.
. I have added remarks about this now, but just ever so briefly. Needs to be expanded on later.