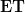 is fully faithful, I should've said that).
]]>
is fully faithful, I should've said that).
]]>
I have a hunch that the following is a characterization of local homeomorphisms (in the way I defined them) of topoi:
is a local homeomorphism if and only if is open and its diagonal
is. Moreover, I believe that if we define a geometric morphism
of infinity topoi to be open if
is an open map of locales (this agrees with the ordinary definition of an open geometric morphism for -topoi), then is 'etale if and only if and its diagonal are open. However, I haven’t thought of how to prove this yet.
]]>@Urs: Thanks again, and fyi: The paper I am writing at the moment is the one establishing a general theory of higher etale stacks.
]]>What you say in #12 seems to me indeed to be a most useful way of thinking about the situation.
I don’t know of course exactly what paper you are about to write, but I’d think in any case in the introduction section it would be great to just sketch transparantly the situation discussed here, maybe in a kind of crisp summary as in Mike’s #2 above, followed by a paragraph with more details as in your #1.
]]>You could write an nLab page about it. (-;
]]>(Also, I am started to question as to whether or not I need to discuss all this in the paper I am writing after all, and was wondering if perhaps it should just be a separate paper entirely? Suggestions/advice? Would an OK tactic be to touch upon it, but then leave further developments for another paper?)
]]>@Urs: Thanks! Do you have any opinion about whether one should view étale maps being the same as the topos as foundational, or the “étalé-space construction” as foundational, as discussed in my last comment?
]]>Hi Dave,
I am certainly looking forward to seeing this stuff written up cleanly. That’ll be foundational.
]]>I may be getting philosophical, but I think that maybe is the fundamental statement, and it is this equivalence which justifies the importance of étale maps. It seems that in some sense that it’s an accident that historically the fundamental statement was for a locale, since this has a mismatch between viewing as a -topos and a -topos at the same time. Indeed, at , the statement for a locale is an interesting and true, and the fact that this holds true for allows us to make the claim that - and then notice that an étale morphism into a localic topos must have a localic domain and correspond to a local homeomorphisms between them. Does anyone have any thoughts?
]]>(-:
]]>Well, I meant more that this was a special case of (which is the “n-ification” of the classical result for ordinary topoi) when
]]>That might be the first time I’ve ever heard a theorem about -toposes referred to as “classical”. Progress marches on, I suppose. (-;
]]>Thanks for the comment about how to typeset é. Anyhow, it should be mentioned that classically defined 'etale maps are still an important class of morphisms, because after all:
For any -topos
However, the theory of -étale morphisms does give a nice explanation as to why is an -category (since apriori one would expect it to be an -category, as it is the slice of one). The real statement is that
where refers to taking only -étale morphisms, and whereby is the functor which promotes an -topos to an -topos. (The notation is suggestive since, at least for this is equivalent to taking sheaves on regarded as an -site with its canonical topology. For this is problematic however (since an -topos is not always sheaves over itself) so by convention the functor is the identify, but I digress…) Now, when there is no difference between -étale and étale, and so this reduces to the classical fact that etale maps over an -topos is equivalent to the -topos in question. When then we have that which in turn is equivalent to the full subcategory of spanned by -truncated objects, hence an -category, and the -truncated objects in are precisely the étale ones! Phew! That was a bit more complicated to spell out than I thought!
]]>I was looking for one more akin to the “slice free” characterization of etale maps
Ah. Well, I can’t think of any. (-:
BTW, you’ve probably noticed this by now, but the TeX syntax \'e for é doesn’t work here. You can write a literal é if you have a way to input Unicode, or (if you use the “Markdown+Itex” format option, which you really should), you can write the HTML é.
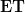 is fully faithful, I should've said that).
]]>
is fully faithful, I should've said that).
]]>
 -topos
-topos 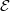 , it has a canonical topology, so we have the
, it has a canonical topology, so we have the 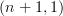 category of sheaves of
category of sheaves of  -groupoids over
-groupoids over 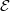 (i.e. it's associated
(i.e. it's associated 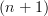 -topos. We also have the
-topos. We also have the 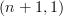 -category
-category 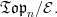 There is a canonical functor
There is a canonical functor 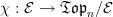 given by slicing. The left Kan extension
given by slicing. The left Kan extension 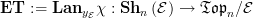 of
of 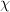 along the yoneda embedding
along the yoneda embedding 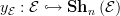 exists as we write it as
exists as we write it as 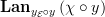 where
where 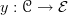 is the Yoneda embedding associated to any
is the Yoneda embedding associated to any  -site of definition for
-site of definition for 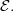 Local homeomorphsms are precisely those in the essential image of
Local homeomorphsms are precisely those in the essential image of 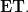 (This is like a topos-theoretic \'etal\'e space construction.)
]]>
(This is like a topos-theoretic \'etal\'e space construction.)
]]>
 -\'etale maps, etc. It's nice to hear that you thought of the same solution, so I'm reassured that it was a good call.
-\'etale maps, etc. It's nice to hear that you thought of the same solution, so I'm reassured that it was a good call. 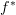 has an additional left adjoint
has an additional left adjoint 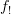 with special properties...).
]]>
with special properties...).
]]>
On the other hand, one might argue that we should define an “-local-homeomorphism” to be a morphism of -topoi that is equivalent to slicing over an -truncated object. Then the existing definitions of local homeomorphism for 0-topoi and 1-topoi would both be special cases of 1-local-homeomorphisms, while the “correct” notion of local homeomorphism between -topoi that you are advocating would be an -local-homeomorphism. That way, the existing terminology could be maintained, according to the general principle that an unprefixed “foo” is equivalent to a “1-foo”.
As for a characterization internal to 1-topoi of the 2-local-homeomorphisms, shouldn’t they be the geometric morphisms where is equivalent to the topos of internal diagrams on some internal groupoid in ?
]]>That’s interesting! In summary, the point is that you can’t define local homeomorphisms between n-toposes to be slice categories unless you move up to their associated -toposes. This is clear when n=0, which is an essential case because it’s where the terminology ’local homeomorphism’ comes from, but it also implies that the usual definition of local homeomorphism for 1-toposes (as found, for instance, in the Elephant), is wrong. Is that an accurate summary?
I don’t think I’ve heard this mentioned before, and I’d probably remember if I had. Terminology-wise, I think I’d be in favor of using the term ’local homeomorphism’ correctly, even if it doesn’t agree with previous usage.
]]> -topoi. I have a suspicion that it must have been noticed before (at least for
-topoi. I have a suspicion that it must have been noticed before (at least for 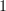 -topoi), and if this is true, please view this discussion, in particular, as a reference request.
-topoi), and if this is true, please view this discussion, in particular, as a reference request.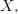 if
if 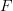 is a sheaf, it has an \'etal\'e space
is a sheaf, it has an \'etal\'e space 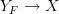 which is a local homeomorphism over
which is a local homeomorphism over 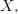 and sections of it are exactly the sheaf
and sections of it are exactly the sheaf 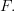 The \'etal\'e space construction yields an equivalence of categories
The \'etal\'e space construction yields an equivalence of categories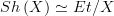 between the category of sheaves on
between the category of sheaves on  and the category of local homeomorphisms over
and the category of local homeomorphisms over  Moreover, assuming
Moreover, assuming  is sober, since sober topological spaces embed fully faithfully into topoi, for a sheaf
is sober, since sober topological spaces embed fully faithfully into topoi, for a sheaf 
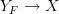 corresponds to a geometric morphism
corresponds to a geometric morphism 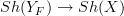 and there turns out to be an equivalence of topoi
and there turns out to be an equivalence of topoi 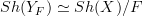 under which this geometric morphism is equivalent to the one induced by slicing:
under which this geometric morphism is equivalent to the one induced by slicing: 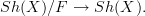
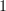 -topoi
-topoi  is *\'etale* if it is equivalent to one of the form
is *\'etale* if it is equivalent to one of the form 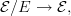 and this was to be a ``local homeomorphism'' of
and this was to be a ``local homeomorphism'' of 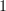 -topoi.
-topoi. -topoi the same way, i.e.
-topoi the same way, i.e. is *\'etale* if it is equivalent to one of the form
is *\'etale* if it is equivalent to one of the form 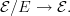
 be a (sober) topological space. In particular, it is a locale, hence a
be a (sober) topological space. In particular, it is a locale, hence a 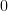 -topos in the sense of Lurie. Lets write this
-topos in the sense of Lurie. Lets write this 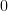 -topos by
-topos by 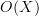 (as it is in fact the lattice of opens of
(as it is in fact the lattice of opens of 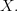 ) The maps of locales that are induced by slicing are exactly those which correspond to inclusions of open sublocales. So, an \'etale map of
) The maps of locales that are induced by slicing are exactly those which correspond to inclusions of open sublocales. So, an \'etale map of 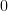 -topoi does not correspond to a local homeomorphism (but it is a particular kind of local homeomorphism).
-topoi does not correspond to a local homeomorphism (but it is a particular kind of local homeomorphism).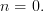
 -topos
-topos 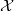 is *
is * -localic* if it is equivalent to
-localic* if it is equivalent to  -sheaves on an
-sheaves on an  -site. There is a functor from
-site. There is a functor from  -topoi to
-topoi to  -topoi which is fully faithful and whose essential image is
-topoi which is fully faithful and whose essential image is  -localic
-localic  -topoi, and if
-topoi, and if 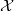 is an
is an  -localic, the
-localic, the  -topos which is corresponds to is the
-topos which is corresponds to is the 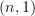 -category of
-category of 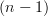 -truncated objects of
-truncated objects of 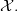
 is an object of an
is an object of an 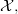 then
then 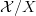 is also
is also  -localic *if and only if*
-localic *if and only if*  is
is  -truncated. So let
-truncated. So let  be an object of
be an object of 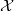 which is
which is  -truncated but not
-truncated but not 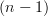 -truncated. Then the \'etale map of
-truncated. Then the \'etale map of  -topoi
-topoi 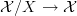 is a morphism between
is a morphism between  -localic
-localic  -topoi. Let
-topoi. Let 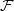 denote the
denote the  -topos associated to
-topos associated to 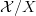 and
and 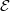 the one associated to
the one associated to 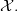 Since
Since  -topoi embed fully faithfully into
-topoi embed fully faithfully into  -topoi as
-topoi as  -localic
-localic  -topoi, this \'etale map induced by
-topoi, this \'etale map induced by 
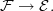 However, it cannot be an \'etale map of
However, it cannot be an \'etale map of  -topoi, since the object
-topoi, since the object  is not
is not 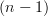 -truncated. Nonetheless, such a geometric morphism is the "correct" notion of a local homeomorphism since if we let
-truncated. Nonetheless, such a geometric morphism is the "correct" notion of a local homeomorphism since if we let 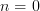 , this is a local homeomorphism of locales, in the usual sense.
, this is a local homeomorphism of locales, in the usual sense.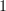 -topoi and is there a name for such geometric morphisms (and is there a characterization of them internal to
-topoi and is there a name for such geometric morphisms (and is there a characterization of them internal to 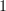 -topoi?)
]]>
-topoi?)
]]>