Based on some feedback that I got behind the scenes, I have now rearranged the material, to make it more light-weight at the beginning.
the section Properties now has the central properties one can deduce for a Bousfield localization that do not require combinatorial model category technology
the section Existence of ... has the existence result for the combinatorial case pretty much as before, but minus the material that has been moved to "Properties"
and the Definition section is now such that it downplays the "derived hom"
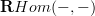 and instead tends to arrange things such that they are properly cofibrant or fibrant . Because it was suggested to me that invoking the derived hom concept makes this look, to the non-expert reader- much more arcane than it is.
and instead tends to arrange things such that they are properly cofibrant or fibrant . Because it was suggested to me that invoking the derived hom concept makes this look, to the non-expert reader- much more arcane than it is.
I just hope that the interconnecting logic between the paragraphs is now still consistent. I fddled a bit with adjusting the statements to the slightly changed assimptions.
]]>