I am wondering about the following:
there is a Quillen adjunction 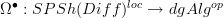 that sends an oo-stack on the cat of manifolds to its deRham algebra.
that sends an oo-stack on the cat of manifolds to its deRham algebra.
Moreover, there is a theorem that says that the left Bousfield localization 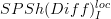 of
of 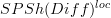 at all the cylinder projections
at all the cylinder projections 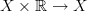 is Quillen equivalent to
is Quillen equivalent to 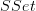 .
.
Let 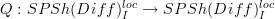 be cofibrant replacement in this localized structure. Then we get the composite functor
be cofibrant replacement in this localized structure. Then we get the composite functor 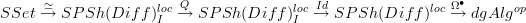 .
.
Looking at what this does on objects, it seems it should be related to the Sullivan-forms functor 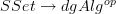 . Has anyone thought about this or seen other people think about it?
. Has anyone thought about this or seen other people think about it?