Okay, now I'll come back to this discussion here.
I am beginning to think that the morphism that we are looking for above, that from some object  in an (oo,1)-topos to some other object
in an (oo,1)-topos to some other object 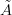 , such that postcomposition with this map maps
, such that postcomposition with this map maps  -valued cohomology to something like the corresponding "Chern character" is essentially the morphism
-valued cohomology to something like the corresponding "Chern character" is essentially the morphism 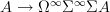
from  to the free stabilization of its suspension.
to the free stabilization of its suspension.
Or more precisely, as I indicated above, the construction is this:
let 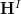 by the arrow category of the smooth ambient (oo,1)-topos. For
by the arrow category of the smooth ambient (oo,1)-topos. For ![[X \hookrightarrow \Pi(X)] [X \hookrightarrow \Pi(X)]](/extensions/vLaTeX/cache/latex_2340f38f94f75249699bd2a47715c835.png) the object in
the object in 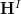 given by the inclusion of
given by the inclusion of  into its path oo-groupoid, and
into its path oo-groupoid, and ![[A \to *] [A \to *]](/extensions/vLaTeX/cache/latex_5aec67504caef8af7b754c193328c386.png) the map to the terminal object, we have that ordinary
the map to the terminal object, we have that ordinary  -cohomology of
-cohomology of  with coefficients in
with coefficients in 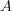 may be expressed in
may be expressed in 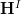 as
as ![\mathbf{H}(X,A) \simeq \mathbf{H}^I([X \to \Pi(X)], [A \to *]) \mathbf{H}(X,A) \simeq \mathbf{H}^I([X \to \Pi(X)], [A \to *])](/extensions/vLaTeX/cache/latex_56495bb63de2bca9352332afff954892.png) .
.
Now let 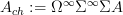 be the stabilization of the suspension object of
be the stabilization of the suspension object of 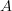 . The morphism
. The morphism 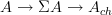 in
in 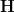 induces a morphism
induces a morphism ![[A \to *] \to [* \to A_{ch}] [A \to *] \to [* \to A_{ch}]](/extensions/vLaTeX/cache/latex_b732b5501f02df63e5c0912536bbd4f1.png) in
in 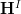 . So we get a morphism in cohomology
. So we get a morphism in cohomology
![\mathbf{H}(X,A) \to \mathbf{H}^I([X \to \Pi(X)], [*\to A_{ch}]) \mathbf{H}(X,A) \to \mathbf{H}^I([X \to \Pi(X)], [*\to A_{ch}])](/extensions/vLaTeX/cache/latex_3a4667ca6aacc20de7417d81520bb779.png) .
.
A cocycle in the thing on the right is a flat differential (i.e. on 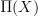 )
) 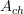 cocycle, whose underlying ordinary cocycle (i.e. on
cocycle, whose underlying ordinary cocycle (i.e. on  ) is trivial. This makes this a cocycle in the "real-ization" of
) is trivial. This makes this a cocycle in the "real-ization" of  : to see what I mean consider the archetypical case for instance that
: to see what I mean consider the archetypical case for instance that 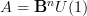 . Then an object in
. Then an object in ![\mathbf{H}^I([X \to \Pi(X)], [*\to A_{ch}]) \mathbf{H}^I([X \to \Pi(X)], [*\to A_{ch}])](/extensions/vLaTeX/cache/latex_fc38f70c4395725becba9ec2bd0a7235.png) is effectively a cocycle in
is effectively a cocycle in 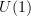 -Deligne cohomology whose 0-form part trivializes. But that's then the same as an
-Deligne cohomology whose 0-form part trivializes. But that's then the same as an 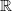 -Deligne cocycle (since the differential forms don't see the nontrivial topology of the coefficient object, only the 0-form part does, if we kill that, we are left with the real version).
-Deligne cocycle (since the differential forms don't see the nontrivial topology of the coefficient object, only the 0-form part does, if we kill that, we are left with the real version).
So there is an object 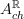 such that
such that
![\mathbf{H}^I([X \to \Pi(X)], [* \to A_{ch}])\simeq\mathbf{H}(\Pi(X), A_{ch}^{\mathbb{R}}) \mathbf{H}^I([X \to \Pi(X)], [* \to A_{ch}])\simeq\mathbf{H}(\Pi(X), A_{ch}^{\mathbb{R}})](/extensions/vLaTeX/cache/latex_61df765f6c07edb12c2e650727721bc2.png)
I think. On the right we have a souped-up version of deRham cohomology. I think we may apply the deRham theorem for oo-groupoids to it to pass to a souped-up version of equivalent real cohomology. But since for the present purpose this just amounts to more notation, let me not do it. Then the punchline is that I am saying that the full generalization of the "Chern cheracter" that in ordinary differential cohomology would be suposed to map an Eilenberg-Steenrod cohomology theory 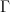 to ordinary real cohomology with coefficients in
to ordinary real cohomology with coefficients in 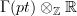 is the composite of the above maps
is the composite of the above maps
![H(X,A) \simeq H^I([X\to \Pi(X)], [A\to *]) \to H^I([X \to \Pi(X)], [* \to A_{ch}]) \simeq H(\Pi(X),A_{ch}^\mathbb{R}) \,. H(X,A) \simeq H^I([X\to \Pi(X)], [A\to *]) \to H^I([X \to \Pi(X)], [* \to A_{ch}]) \simeq H(\Pi(X),A_{ch}^\mathbb{R}) \,.](/extensions/vLaTeX/cache/latex_49eeae4666bd4dc9c3be18567cec3d72.png)
Here is something to check this statement. I am beginning to think the following is true, but I don't have a full proof yet:
for  the oo-Lie groupoid of
the oo-Lie groupoid of  let
let 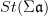 be the oo-Lie groupoid of the stabilization of
be the oo-Lie groupoid of the stabilization of 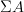 . Then I think the Chevalley-Eilenberg algebra (schreiber)
. Then I think the Chevalley-Eilenberg algebra (schreiber) 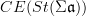 is the algebra of invariant polynomials on
is the algebra of invariant polynomials on  .
.
I was looking for such a completely intrinsic oo-categorical definition of invariant polynomials for a while, and now I think this is it. But I still need to think about it.
Notice that, if right, this means for instance that for 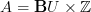 (the coefficient object for degree 0 K-theory) we have that
(the coefficient object for degree 0 K-theory) we have that 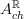 is the oo-Lie groupoid integrating the oo-Lie algebroid whose CE-algebra is that of invariant polynomials on
is the oo-Lie groupoid integrating the oo-Lie algebroid whose CE-algebra is that of invariant polynomials on  . But that's
. But that's 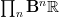 , hence the above generalized Chern-character for
, hence the above generalized Chern-character for 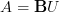 would take values in even graded real cohomology, which is the right answer.
would take values in even graded real cohomology, which is the right answer.
Hm, Ill better stop here and dicsuss this in more detail on my web. I'll also have a look at the entry on your web now.
]]>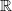 in various degrees, something like
in various degrees, something like 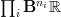 such that the entire real cohomology content of
such that the entire real cohomology content of 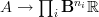 and then the Chern character map should be postcomposition with this morphism. I'd think.
and then the Chern character map should be postcomposition with this morphism. I'd think.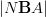 not to the constant simplicial presheaf
not to the constant simplicial presheaf 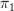 of each of them can be identified with
of each of them can be identified with 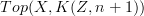 and
and 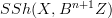 , respectively, and thereby with
, respectively, and thereby with 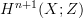 , and similarly for all higher homotopy groups. So all we need is a map inducing those isomorphisms. Perhaps there is an adjunction.
, and similarly for all higher homotopy groups. So all we need is a map inducing those isomorphisms. Perhaps there is an adjunction.