The canonical topology is not the unique topology, but it is the unique topology which contains all other topologies for which the representables are sheaves. In that sense it is determined uniquely. By contrast there can be many 'canonical' transformations between two given functors with nothing to single out any of them.
Yes, the canonical topology is not the unique topology, but it is the unique topology satisfying a certain property.
Similarly, the non-identity canonical morphism 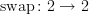 is not the unique morphism
is not the unique morphism 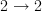 , but it is the unique morphism satisfying a certain property. (There are many ways to state this property: it is a derangement, it is not the identity, it is equal to
, but it is the unique morphism satisfying a certain property. (There are many ways to state this property: it is a derangement, it is not the identity, it is equal to 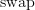 , etc.) Also, the canonical transformation
, etc.) Also, the canonical transformation  is not the unique canonical transformation
is not the unique canonical transformation 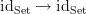 , but it is the unique transformation satisfying a certain property.
, but it is the unique transformation satisfying a certain property.
In contrast, the two noncanonical morphisms 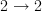 cannot be characterised uniquely using non-evil language (although that is hard to make precise).
cannot be characterised uniquely using non-evil language (although that is hard to make precise).
The best sense that I can make of what you're saying here is that ‘canonical’ should only come after ‘the’, never after ‘a’. In any given situation, we may (if we wish) state some property that is satisfied by at most one thing, and declare that thing to be ‘canonical’. We can do this completely arbitrarily, as long as the thing that we pick is uniquely determined by the data at hand, but we can only do it once. So it doesn't make sense to define ‘canonical’ in general, since then there are many situations in which we have chosen canonical things. Instead, we must use a family of ad hoc definitions, to pick (at most) one thing out in each context. Is this what you mean?
If so, my reply is that the general notion of ‘canonical’ is used in a grammatically different way (following ‘a’, not ‘the’) which should not cause confusion; but it is related, since only a canonical thing can be uniquely specified by the data at hand so that you can define it to be the canonical thing.
"Equivariant" is used pretty widely, but I'm only aware of one basic meaning, namely respecting the actions of some group. Are there others?
Not that I know of, but the concept of canonical morphism applies in a more specific situation, when one automorphism group acts (on both sides) on another via a couple of functors. I'm worried that ‘equivariant morphism’ (a term which certainly exists already) might be applied to some other group actions in this situation. But perhaps there are no other group actions likely to be thought of.
]]>
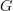 on objects of a category
on objects of a category  , then this is two functors from
, then this is two functors from 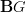 to
to  , and a canonical morphism between these is precisely a
, and a canonical morphism between these is precisely a 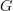 -equivariant morphism between the original representations of
-equivariant morphism between the original representations of 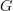 . The general concept is a straightforward generalistion of this. So there probably is no room for confusion.
. The general concept is a straightforward generalistion of this. So there probably is no room for confusion.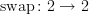 is not the unique morphism
is not the unique morphism 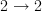 , but it is the unique morphism satisfying a certain property. (There are many ways to state this property: it is a derangement, it is not the identity, it is equal to
, but it is the unique morphism satisfying a certain property. (There are many ways to state this property: it is a derangement, it is not the identity, it is equal to 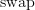 , etc.) Also, the canonical transformation
, etc.) Also, the canonical transformation  is not the unique canonical transformation
is not the unique canonical transformation 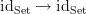 , but it is the unique transformation satisfying a certain property.
, but it is the unique transformation satisfying a certain property.