We should still call it the classifying space of a category, because, as your boss points out,
I heard that. May I still disagree? Don't tell him! ;-)
the classifying space of a category C classifies the C-torsors.
Yeah, but every space X classifies something, namely 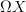 -torsors. My impression is that the Moerdijk category-torsors are torsors over the oo-groupoid fibrantly replacing the category, that's why these spans appear. They form the groupoidification of the category. And this means that the result really has nothing intrinsically to do with the original category. As we discussed with Mike recently, in the context of the notion of "cohomology of a category".
-torsors. My impression is that the Moerdijk category-torsors are torsors over the oo-groupoid fibrantly replacing the category, that's why these spans appear. They form the groupoidification of the category. And this means that the result really has nothing intrinsically to do with the original category. As we discussed with Mike recently, in the context of the notion of "cohomology of a category".
But in any case, even if we were interested for other reasons in such torsors, it's not these torsors that play a role in the discusison of test categories. I think it only is good style to call something a classifying object if one was previously talking about the things it classifies. Otherwise I could call every object whatsoever a classifying object. When you ask me what it classifies, I just say it classifies the homotopy fibers of morphisms into it. That's always true. But can be besides the point.
Anyway, I won't fight over this terminological issue. But I will want to add at least some clarifying remarks to the entry classifying space, sometime later.
]]>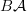 of a category
of a category 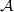 you mean (the realization of) its nerve, right?
you mean (the realization of) its nerve, right?