Domenico,
yes, I agree, that's a way to put it.
But maybe we can start out saying that a priori all of 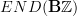 acts on
acts on 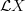 , while the "circle action" proper is only the part
, while the "circle action" proper is only the part 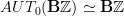 . Because the other parts of
. Because the other parts of 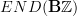 will have a role to play, too. As we said, the
will have a role to play, too. As we said, the 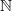 -grading on
-grading on 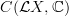 is induced from the action of what on the homology
is induced from the action of what on the homology 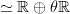 of the circle acts by
of the circle acts by 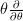 , while the differential is that induced by
, while the differential is that induced by 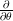 . The first, even, Lie algebra element should correspond to nontrivial objects in
. The first, even, Lie algebra element should correspond to nontrivial objects in 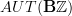 .
.
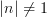 we just have a group homomorphism, not an automorphism.
we just have a group homomorphism, not an automorphism.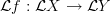 is equivariant with respect to the categorical circle action (this should be almost immediate)
is equivariant with respect to the categorical circle action (this should be almost immediate)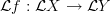 is just post-composition with
is just post-composition with 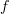 :
: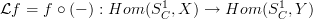
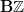 as a model for what could also be modeled as
as a model for what could also be modeled as 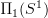 then:
then: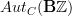 -- labeled by some
-- labeled by some 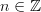 -- describe maps from the circle onto itself that fix the basepoint and have winding number
-- describe maps from the circle onto itself that fix the basepoint and have winding number 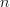
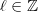 -- describe a rigid rotation of the loop
-- describe a rigid rotation of the loop 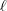 -times around the circle.
-times around the circle.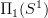 explicit. That will produce a situation that looks much more like the naive circle action that one expects. But together probably both models illustrate nicely how we have to distinguish here between automorphisms of the circle (maps with winding number) and genuine rotations of the circle.
explicit. That will produce a situation that looks much more like the naive circle action that one expects. But together probably both models illustrate nicely how we have to distinguish here between automorphisms of the circle (maps with winding number) and genuine rotations of the circle.