apparently, there's a little inconsistency on the definitin of objects in
An object in 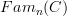 is a functor
is a functor 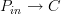 , but a morphism then is a natural transformation between the functors
, but a morphism then is a natural transformation between the functors 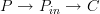 and
and 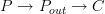 . The components of this natural transformation is itself a functor
. The components of this natural transformation is itself a functor ![P \to [I,C] P \to [I,C]](/extensions/vLaTeX/cache/latex_b97062ac10c85ae7c6951e613f27770e.png) . That's what I meant to express. But should be clarified.
. That's what I meant to express. But should be clarified.
this should be what Urs wonders about in the query box, am I right?
This is certainly one aspect, and not the least one, yes. However, the central aspect that I was driving at is this potential reformulation of the discussion where 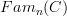 appears explicitly to a discussion where it just appears implcitly as a way to express the extension of a functor out of
appears explicitly to a discussion where it just appears implcitly as a way to express the extension of a functor out of 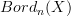 to a functor just out of
to a functor just out of 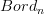 .
.
I agree with your query box comment that this is somehow about "representable" QFTs in some sense. Indeed, a sigma-model QFT should be thought of as a QFT that is "represented" by a geometric object in some sense. Precisely in which sense, though, is part of the question, still.
I should also say that I intentionally just wrote "extension" instead of "Kan extension". While in some toy examples Kan extension seems to lead to the right answer, in other toy examples it seems to lead to an unexpected answer. I am currently not really sure what kind of extension it is. Possibly it is a Kan extension all right, but only if one takes due care of doing the right higher categorical Kan extension. Unfortunately I have very little technical control over (oo,1)-categorical Kan extensions, let alone (oo,n)-categorical ones. Even HTT gives only a partial discussion of (oo,1)-Kan extensions. And model category theoretic models seem not much better understood.
This is currently my main technical stumbling block here. Also notice that the article by Freed/Hopkins/Lurie/Teleman is at best vague about what their integration functor 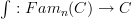 (which by my conjectural idea should somehow compute this extension ) does on morphisms. On objects its the (oo,n)-categorical colimit, but on morphisms it is less clear.
(which by my conjectural idea should somehow compute this extension ) does on morphisms. On objects its the (oo,n)-categorical colimit, but on morphisms it is less clear.
Johan Alm looked into this in some detail for the plain 1-categorical context. The trouble is that the obvious abstract-nonsense definition for what happens on morphisms is not functorial. One can "fix" it by hand, though. But not uniquely. One way to fix it yields effectively a generalizations of John Baez's "degroupoidification" map (he implcitly considers the special case where the objects in 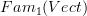 are functors constant on the ground field). It turns out though that there is at least one other way to write down a functorial formula that restricts to taking colimits on objects. With this trouble already present in the 1-categorical case, I am currently left a little puzzled about how the integration functor is properly defined in general higher categorical case.
are functors constant on the ground field). It turns out though that there is at least one other way to write down a functorial formula that restricts to taking colimits on objects. With this trouble already present in the 1-categorical case, I am currently left a little puzzled about how the integration functor is properly defined in general higher categorical case.
]]>
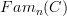 -description, right.
-description, right.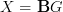 .
.
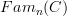 is a functor
is a functor 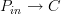 , but a morphism then is a natural transformation between the functors
, but a morphism then is a natural transformation between the functors 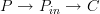 and
and 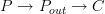 . The components of this natural transformation is itself a functor
. The components of this natural transformation is itself a functor ![P \to [I,C] P \to [I,C]](/extensions/vLaTeX/cache/latex_b97062ac10c85ae7c6951e613f27770e.png) . That's what I meant to express. But should be clarified.
. That's what I meant to express. But should be clarified.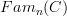 appears explicitly to a discussion where it just appears implcitly as a way to express the extension of a functor out of
appears explicitly to a discussion where it just appears implcitly as a way to express the extension of a functor out of 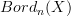 to a functor just out of
to a functor just out of 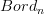 .
.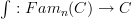 (which by my conjectural idea should somehow compute this extension ) does on morphisms. On objects its the (oo,n)-categorical colimit, but on morphisms it is less clear.
(which by my conjectural idea should somehow compute this extension ) does on morphisms. On objects its the (oo,n)-categorical colimit, but on morphisms it is less clear.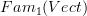 are functors constant on the ground field). It turns out though that there is at least one other way to write down a functorial formula that restricts to taking colimits on objects. With this trouble already present in the 1-categorical case, I am currently left a little puzzled about how the integration functor is properly defined in general higher categorical case.
are functors constant on the ground field). It turns out though that there is at least one other way to write down a functorial formula that restricts to taking colimits on objects. With this trouble already present in the 1-categorical case, I am currently left a little puzzled about how the integration functor is properly defined in general higher categorical case.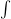 and references on that topic.
and references on that topic.