Am I mixed up? Let me see.
We have a double complex 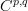 with one differential increasing
with one differential increasing 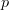

and the other decreasing 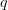
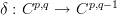
This gives me single differential
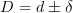
of definite degree (say +1) if the total degree is taken to be 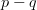 .
.
So if both 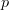 and
and 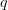 ranged in
ranged in 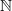 this gives degrees in all of
this gives degrees in all of 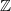 .
.
And I'd think this is what I get from forming the chain complex of a cosimplicial simplicial abelian group: a chain complex (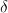 ) of cochain complexes (
) of cochain complexes (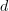 ).
).
Do you agree?
]]>![\Delta \to [\Delta^{op}, Ab] \Delta \to [\Delta^{op}, Ab]](/extensions/vLaTeX/cache/latex_d1cc8ee3ed1bc3649a9309085cdbd8e6.png)
![\Delta \to [\Delta^{op}, CRing] \Delta \to [\Delta^{op}, CRing]](/extensions/vLaTeX/cache/latex_5d63c4f0c914aa3a558311cfc687015e.png)