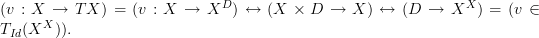I'm beginning to get a feel for how I want the seminar to go. The colloquium series here goes by the name of "Mathematical Pearls". My abstract can be found here (none of you suggested a diagram so I had to invent something suitably daft!). My current sketch plan is:
First, the disclaimer. This isn't history and I'm no expert. This is more "how it might have been".
First irritating thing: you can't talk about "the set of all sets". EM wanted to do so to talk about cohomology theories and specifically operations on cohomology theories. So they invented "categories" to allow them to do so. The "deal with Russell" (i.e. avoiding the paradox) was that they would steer clear of anything that might bring them close to the paradox. This leads one naturally to avoid examining objects too closely and concentrating on morphisms.
Second irritating thing: group-like things crop up everywhere, such as in homotopy groups, and it's annoying to have to keep proving the same things over and over again. If we could only have a "platonic group" for which we could prove stuff once and for all, we wouldn't have to keep doing it over and over again. Lawvere gave us such, and it means that we can use Eckman-Hilton to prove that
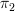 is abelian rather than the complicated shuffle homotopy. (I quite like that shuffle, but I won't say so!)
is abelian rather than the complicated shuffle homotopy. (I quite like that shuffle, but I won't say so!)So we can talk about "group objects" in (almost) any category. But clearly, there's nothing special about groups. We can do the same for rings, modules, monoids, Banach spaces ... huh? Banach spaces??? How did they creep in there? Then explain that Banach spaces are (almost) algebraic and that
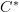 -algebras actually are.
-algebras actually are.There's categories everywhere. Once you have "categorical glasses" on then you can't help seeing categories anywhere and everywhere. Groups, posets, lattices, metric spaces ... huh?
But I still feel that I'm missing something for the ending. I agree that Yoneda is extremely important, and I like the recasting of differential equations in categorical form, but of the above (and I haven't looked at Vaughan's list yet), Todd's is the closest to what I want. Describing or recasting isn't quite the dramatic conclusion that I'm after. I'll take a look at Vaughan's list to see if anything jumps out at me.
Incidentally, there'll be a fair few algebra people there as well.
]]>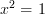 for all
for all  is interpretable in any category with finite products, and that product-preserving functors
is interpretable in any category with finite products, and that product-preserving functors 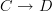 always map such a structure in
always map such a structure in  to such a structure in
to such a structure in  . Then I produced a series of product-preserving functors
. Then I produced a series of product-preserving functors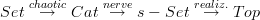
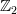 in
in 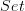 over to the total space
over to the total space 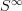 of the classifying bundle of
of the classifying bundle of 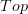 . This structure is connected, and: we're done! Simple. It was a leisurely-paced talk and went over well with the functional analysts in the crowd.
. This structure is connected, and: we're done! Simple. It was a leisurely-paced talk and went over well with the functional analysts in the crowd.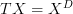
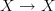 starting at the identity map: with our category theory this is now just the hom-adjunction in the cartesian closed category:
starting at the identity map: with our category theory this is now just the hom-adjunction in the cartesian closed category: