I have a pedagogic reaction to that, so I think that that is the end point of an exposition rather than the initial one. I have given lots of talks on h.c. diagrams and have found that people (i.e. mathematicians, even algebraic topologists, who are not au fait with the ideas) are even amazed how they arise in that simple situation where you have take a commuting triangle of spaces, and maps, and replace each space by homotopy equivalent one. i.e. bare hands work! There are lots of such people and if they face a high cliff of ideas to face up to the concept then they will shut it out. I therefore suggest that we put the ideas that you suggest towards the end of a discussion so that the bare hands stuff helps 'people' to understand functors between (oo,1)-categories.
I faced a lot of opposition from the mathematical 'nomenclatura' when I tried to get grants to follow the quasicategory line in the 1980s. (As I repeat, Jean-Marc and I sketched out the basics on a walk on Anglesey in about 1984 or there abouts. We applied but did not get funding and the extreme reaction against the ideas from some referees was very hurtful. We did try to do too much using simplicial enriched categories rather than quasicategories as we thought the latter would not be accepted at that time. Now things may be different and the homotopy theorists are much more positive about this viewpoint.
So as yet I think of h.c. as a way to explain the (oo,1)-terminology and to give a feel of why that is useful and very important.I may be wrong but I remember a reaction of an influential professor when I explained crossed complexes in terms of simplicial groups and as he understood where those lay in relation to stuff he knew, he was happy. I think it expedient to start where those 'people' are and make them feel they understand where we are rather than to go too quickly to the elegant approach.
That is the pedagogic reply, now the maths. I believe that what you say is completely right. I feel that one thing the h.c. nerve does is link up the bar construction more explicitly with other notions of h.c. There is a mysterious reference by Dwyer and Kan to the simplicial resolution as giving infinitely homotopy commutative diagrams, as if that was obvious, and to me there was a lot of detail to check and to check explicitly.
]]>
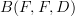 is not just any cofibrant replacement, it is a universal cofibrant replacement. (I've been reading a bit of Richard Garner's A homotopy-theoretic universal property of Leinster's operad for weak
is not just any cofibrant replacement, it is a universal cofibrant replacement. (I've been reading a bit of Richard Garner's A homotopy-theoretic universal property of Leinster's operad for weak  -categories and feel he makes some very pertinent remarks on cofibrant replacements and on arguing for choosing them canonically; see the discussion on page 2.)
-categories and feel he makes some very pertinent remarks on cofibrant replacements and on arguing for choosing them canonically; see the discussion on page 2.)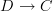 is that it is a model for a functor of (oo,1)-categories.
is that it is a model for a functor of (oo,1)-categories. .
.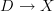 (
( a simplicial category) to be a simplicial functor
a simplicial category) to be a simplicial functor 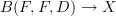 where
where 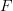 is the free category on a graph monad, and
is the free category on a graph monad, and