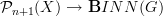Butterflies (which in n-lab speak are ......?
a butterfly is a butterfly is a butterfly... :-)
Butterflies are just a way to present morphisms in 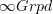 between one-object 2-groupoids.
between one-object 2-groupoids.
At least in my set-up, it's a bit simpler:
Even simpler?!
Can you write into some entry precisely what you have in mind?
]]>So I expect a general 2-bundle to be a gerbe over some suitable cover, like the total space of a principal bundle.
Indeed. There is described in the second section at string structure. In my last article with Stasheff and sati we call this "local semi-trivialization": instead of pzulling back the 2-bundle to its own total space where it trivializes, one pulls it back just to a covering spaces, where it jusgt b ecomes a bit simpler.
]]>By the way: somebody wrote at principal 2-bundle that while that concept is more general than that of gerbe, that of gerbe could "easily be generalized to match".
I am not so sure about this. If you start generalizing the simple statement "locally non-empty and connected stack" such that it describes sections of general 2-bundles, you have to say things that effectively make you say "principal 2-bundle" and no longer say "gerbe".
]]>There is a second part of Butterflies: ArXiv 0910.1818. I have added a link to the entry.
Thanks. I added a remark on terminology to this at butterfly and then added the reference also to principal 2-bundle.
]]><blockquote><bockquote >I was only looking at 2-connected covers, originally. </blockquote><br /><br />this is interesting, since it perfectly agrees with the geometric picture I was trying to describe in the posts above: functors <latex >\mathcal{P}_1(X)\to \mathbf{B}G</latex> lift to functors <latex >\mathcal{P}_2(X)\to Something</latex>, and this something one has to expect to be the 2-connected cover of <latex >\mathbf{B}G</latex>. <br />it is precisely what I was trying to mean by saying I didn't like the appearance of <latex >INN(G)</latex>, and would have liked a more geometric description on the first spot, which then one could prove to be explicitly given by the INN construction.<br /><br />thanks a lot :-)</bockquote>]]>
Pradines certainly used the term but I am not sure it is in exactly the same context.
I did not know that there was an entry on butterflies!
There is a second part of Butterflies: ArXiv 0910.1818. I have added a link to the entry.
]]>Butterflies (which in n-lab speak are ......?
a butterfly is a butterfly is a butterfly... :-)
Butterflies are just a way to present morphisms in 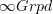 between one-object 2-groupoids.
between one-object 2-groupoids.
There are very close connections with reduction of structure group. In fact in non_abelian cohomology where the construction INN(G) sort of originates is is usual (following Dedecker) to use a 2-group as coefficients or rather the corresponding crossed module in that setting. I have been trying to look at Turaev's homotopy quantum field theory from this point of view, but I find it quite hard going. In algebraic geometry some useful ideas have been emerging with work by Aldrovandi and Noohi on Butterflies (which in n-lab speak are ......? I leave someone else to say because I always choose the wrong term!) Their stuff would seem to be connected with what you are talking about.
]]>and, more in general to a functor \Pi(X)\to \mathbf{B} INN(G): it is a flat \mathbf{B} INN(G)-connection!
Yes, that's the idea, exactly.
]]>But I'm still unable to see this directly. And, most of it, I'm still unable to see a priori that curvature is a globally defined 2-form, despite a connection is so only locally.
Okay, so what you need is the full story of how one derives this.
Let's do the simpler case first, where the coefficient object is a group object. Recall the abstract definition of "abstract de Rham cohomology" not in terms of differential forms, but just in terms of flat oo-bundles whose underlying oo-bundle is trivial. (See the diagrams there.)
Then it is a theorem that we have a fibration sequence
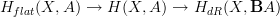 .
.
This allows us to define non-flat differential cohomology with coefficients in A to be the homotopy fiber of 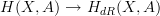 over the given curvature class. This curvature class is by definition of
over the given curvature class. This curvature class is by definition of 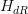 globally defined. Have a look at the link for the case of groupal coefficients.
globally defined. Have a look at the link for the case of groupal coefficients.
fine. so I guess that stackification [,,,]
Yes, that's rigtht.
what I like of this path groupoids point of view is that one talks of connections without differenial forms.
Yes!
What is curvature?
But we said this before: curvature for a transport 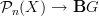 is some transport
is some transport