similarly, whitehead towers
of
are obtained as fibration sequences
yes, very nice. I had made a remark exactly along these lines here, recently.
This needs to be polished and moved to Whitehead tower
]]>I see there’s a new article in this area:
Added a section on effective computation of twisted cohomology using de Rham cohomology of the universal cover and the action of the fundamental group thereon:
The idea was inspired by the following MO answer by Peter Michor.
Would anyone know what to do if the fundamental group is not finite?
]]>Inspired by discussion with Marc Hoyois in another thread I finally went and started trying to beautify the entry twisted cohomology a little.
So far I have
given it a better and considerably expanded Idea-section
given it a better and considerably expanded Definition-section
Especially the Definition section certainly could still do with more work, but for the moment I am out of steam.
Also the Examples-section should be cleaned up and more examples should be added. Maybe later. (Or maybe Marc feels energetic to add more! :-)
]]>added to the section In terms of sections at twisted cohomology a pointer to the fully detailed proof of the statement stated there.
]]>Added an Examples-section
and a brief followup-section
meant to put the construction by Ando-Blumberg-Gepner into perspective.
]]>it seems to me a beautyful example of how the nLab discussions are creating a common point of view on the subject. I really like this.
Yes, I am very much enjoying this, too. Glad to have you around here.
]]>similarly, whitehead towers
of
are obtained as fibration sequences
yes, very nice. I had made a remark exactly along these lines here, recently.
This needs to be polished and moved to Whitehead tower
]]>I agree, twisted K-theory could be presented as the first example in the example section.
My faint memory says that the tensor product issues, hence product for classes, is more delicate in twisted K-theory than in the usual. Is this easy in this approach ?
]]>just let me know your favourite way of receiving comments: query boxes on the page? forum posts?
forum posts would be nice.
query boxes are fine, too, but I will tend to react to them quickly and then remove them. So maybe for a more coherent discussion forum posts would be better. Thanks.
]]>By the way, one reason (of several) why I have little right now is that I need to bring some stuff curently on my personal web into shape. Currently I am busy polishing and expanding the entry path oo-groupoid.
This has developed quite a bit, I think. I'd be interested in hearing your comments on this.
]]>Thanks!
Now I did spent some time working more on twisted cohomology after all:
I edited the beginning, up to where the Examples-section begins:
added a sentence to the Idea-section
made the statements that follow the definition a series of formal propositions with formal proofs
polished the notation a bit here and there, for instance in changing 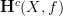 to
to ![\mathbf{H}_{[c]}(X,f) \mathbf{H}_{[c]}(X,f)](/extensions/vLaTeX/cache/latex_06f2dd8bfac4039a75af7fd11b30b356.png) (for it not to collide with the
(for it not to collide with the 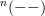 -notation).
-notation).
Yes. Please feel free to replace the nLab entry with what you have. I have no time to work on this at the moment, but I do like what you did.
]]>Thanks, that looks good.
One remark I would have is that the "motivating example" at the beginning is not really an immediate motivation for the definition that follows, as it requires the argument following that in turn to see how it relates. Maybe it would be better to move that alltogether into the examples section.
]]>a major clean up.
That might indeed be a good idea. Thanks!
]]>Yes.
Right, so who is going to put this into the entry now? :-)
I have to run and catch a bus, but maybe I can do it later...
]]>Okay, right, "the fiber of the collection of  -points of
-points of  over a given
over a given  -point of
-point of 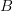 .
.
But maybe then actually proper topos-language is preferable: at stage  , twisted cohomology is the (homotopy) fiber of
, twisted cohomology is the (homotopy) fiber of 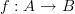 over a given element of
over a given element of 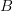 .
.