Okay, thanks. I removed my proof and retained yours.
All right, so coming back to the infinitesimals now.
I still need to write out a fully formal proof that the infinitesimal path oo-groupoid functor 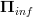 is equivalent to
is equivalent to 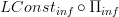 . By analogy with the finite case, for this it is sufficient to show that on representables it has the desired action, namely that it sends some
. By analogy with the finite case, for this it is sufficient to show that on representables it has the desired action, namely that it sends some 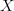 to the presheaf which takes probes of X only after reducing away all infinitesimal directions of the probe object.
to the presheaf which takes probes of X only after reducing away all infinitesimal directions of the probe object.
I started typing something along these lines in the section Properties at infinitesimal interval object, but this needs to be expanded.
For the moment though I need to take care of something else.
]]>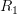 .
.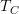 does not match the morphisms in
does not match the morphisms in 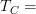
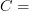
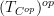 with the structure of a site such that the 0-section
with the structure of a site such that the 0-section 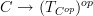 is a morphism of sites.
is a morphism of sites.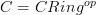 in which case
in which case 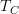 should be thought of as
should be thought of as 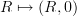 .
.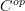 be a site and
be a site and 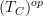 its tangent category. Then we want to put a site structure on
its tangent category. Then we want to put a site structure on 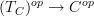 is a morphism of sites. Then this induces a geometric morphism of oo-stack oo-toposes.
is a morphism of sites. Then this induces a geometric morphism of oo-stack oo-toposes.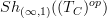 is locally contractible relative to
is locally contractible relative to 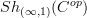 .
.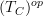 are still sheaves there, which is just what we expect of a topology on "infintiesimally thickened spaces". Then this should imply that we
are still sheaves there, which is just what we expect of a topology on "infintiesimally thickened spaces". Then this should imply that we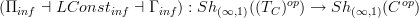 .
.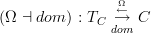
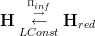
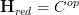 and noticing that under opposing categories left adjoint become right adjoints, and vice versa.
and noticing that under opposing categories left adjoint become right adjoints, and vice versa.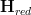 , an (oo,1)-category "of spaces" of sorts, so that
, an (oo,1)-category "of spaces" of sorts, so that 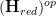 is the category of "function algebras" on these spaces.
is the category of "function algebras" on these spaces.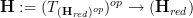 .
.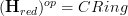 , then
, then 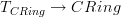 is the category of all modules over all rings, but with each module
is the category of all modules over all rings, but with each module 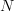 over a ring
over a ring 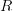 regarded as the square-0-extension ring
regarded as the square-0-extension ring 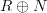 . But this is of course in
. But this is of course in 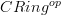 precisely an infinitesimal thickening of the space corresponding to
precisely an infinitesimal thickening of the space corresponding to 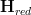 an (oo,1)-topos,
an (oo,1)-topos,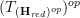 itself an (oo,1)-topos?
itself an (oo,1)-topos?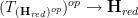 a (essential) geometric morphism?
a (essential) geometric morphism?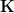 : I renamed that to
: I renamed that to 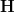 , which is indeed of course a much smoother perspective. The thing it sits over I named
, which is indeed of course a much smoother perspective. The thing it sits over I named 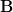 and then
and then 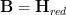 .
.