we need to demonstrate an isomorphism
.
This can't exist. There is a canonical functor the other way round: 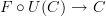 . But it is not an isomorphism (and not an equivalence) in general:
. But it is not an isomorphism (and not an equivalence) in general:
the category 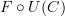 is the category whose objects are those of
is the category whose objects are those of 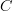 , and whose morphisms are words of composable morphisms in
, and whose morphisms are words of composable morphisms in 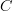 . Composition in
. Composition in 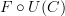 is just concatenation of such words.
is just concatenation of such words.
Now, every such word in composable morphisms can be evaluated to one single morphism in 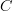 : we we just take all the morphisms in the word and form their composite using the composition rule provided with
: we we just take all the morphisms in the word and form their composite using the composition rule provided with 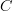 . This assignment
. This assignment 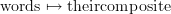 is easily seen to be a functor from
is easily seen to be a functor from 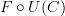 to
to  . This functor is called the counit of the adjunction . Of the adjunction that we are wanting to establish.
. This functor is called the counit of the adjunction . Of the adjunction that we are wanting to establish.
To get that, we should try to explitly say what it is that a functor 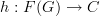 does. Say out in words which data you have to specify in order to describe such a functor
does. Say out in words which data you have to specify in order to describe such a functor 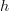 to me.
to me.
Here is a hint: the functor 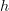 needs to send every morphism in
needs to send every morphism in 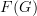 to a morphism in
to a morphism in 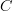 , such that this respects composition. The morphisms in
, such that this respects composition. The morphisms in 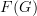 are words of consecutive edges in the graph
are words of consecutive edges in the graph 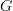 . Their composition operation is just the concatenation of words.
. Their composition operation is just the concatenation of words.
So in particular there are the words of length 1, and the functor 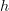 needs to send each of them to some morphism in
needs to send each of them to some morphism in 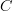 . Suppose this assignment of a morphism in
. Suppose this assignment of a morphism in 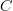 for each morphism in
for each morphism in 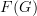 that is a word of length 1 is given. What other information is there needed in order to specify a functor
that is a word of length 1 is given. What other information is there needed in order to specify a functor 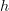 , i.e. in order to specify what it does to words of legnth greater than 1 ? Is there any further information needed? Can we use the functoriality of
, i.e. in order to specify what it does to words of legnth greater than 1 ? Is there any further information needed? Can we use the functoriality of 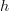 (the fact that it respects composition) in order to deduce what it does to words of length greater than 1?
(the fact that it respects composition) in order to deduce what it does to words of length greater than 1?
The answer is yes. Do you see how this works?
So from this reasoning we find that specifying a functor 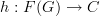 is the same thing as giving a map of sets
is the same thing as giving a map of sets 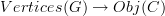 and a map of sets
and a map of sets 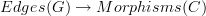 that matches the previous assignment on source and target objects. And nothing else. By functoriality of
that matches the previous assignment on source and target objects. And nothing else. By functoriality of 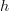 alone it follows that this fixes what
alone it follows that this fixes what 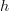 does on all morphisms of
does on all morphisms of 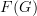 .
.
But what we just specified is manifestly nothing but a map of graphs 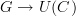 .
.
So functors 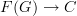 encode precisely the same informaton as morphisms of graphs
encode precisely the same informaton as morphisms of graphs 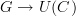 .
.
This is the adjunction isomorphism. We may write it as a bijecton of sets
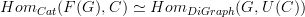 .
.
Do you see what I mean?
(In fact to establish an adjunction we also need to check that this bijection is "natural". But let's not worry about that for the time being.)
]]>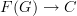 , which graph morphism
, which graph morphism 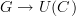 do you send it to? And how do you go the other way round?
do you send it to? And how do you go the other way round?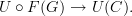
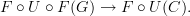
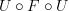 equals (which it doesn't)
equals (which it doesn't) 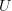 above, the other expression was correct, i.e. it is true that
above, the other expression was correct, i.e. it is true that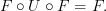
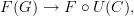
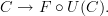
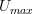 is
is 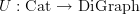 now. What we are after is understanding that for
now. What we are after is understanding that for 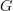 any graph, functors
any graph, functors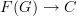
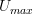 as follows:
as follows: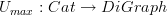 that given a category
that given a category 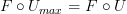 .
.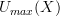 and
and 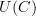 in your latest comment are not equal. But they are also not isomorphic.
in your latest comment are not equal. But they are also not isomorphic.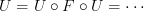
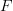 is still the free category functor? Then
is still the free category functor? Then 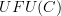 is the graph whose edges are words in the morphisms of
is the graph whose edges are words in the morphisms of 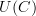 is the graph whose edges are just the morphisms in
is the graph whose edges are just the morphisms in 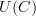 should be. There were two options, he told me the correct one. I accepted it happily. His answer agreed with what David said and is double confirmed by Urs. The "correct" forgetful functor is the one that keeps all composite edges. Fine.
should be. There were two options, he told me the correct one. I accepted it happily. His answer agreed with what David said and is double confirmed by Urs. The "correct" forgetful functor is the one that keeps all composite edges. Fine. and 3 non-identity morphism
and 3 non-identity morphism 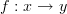 ,
, 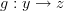 , and
, and 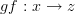 (as above)
(as above)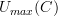 is the directed graph consisting of three nodes and only TWO (non self-looping) edges corresponding to the non-composite non-identity edges. It does not contain an edge corresponding to the morphism
is the directed graph consisting of three nodes and only TWO (non self-looping) edges corresponding to the non-composite non-identity edges. It does not contain an edge corresponding to the morphism 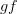 .
.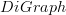 . I used the fact the
. I used the fact the 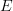 was a functor to prove that
was a functor to prove that 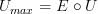 and both
and both 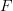 is its adjoint functor to construct an adjoint to
is its adjoint functor to construct an adjoint to 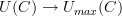 for any category
for any category 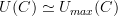
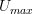 is the same as
is the same as 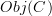 and set of morphisms
and set of morphisms 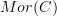 and maps
and maps 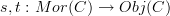 that send each morphisms to its source and target object, and with some composition operation, the underlying directed graph
that send each morphisms to its source and target object, and with some composition operation, the underlying directed graph  and
and 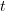 , respectievly.
, respectievly.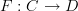 a functor between categories, which is given by some maps of objects
a functor between categories, which is given by some maps of objects 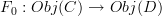 and some maps of morphisms
and some maps of morphisms 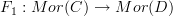 the value of the functor
the value of the functor 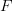 is the morphism of graphs
is the morphism of graphs 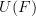 that has precisely the same action, now regarded as a map between sets of vertices and edges of graphs.
that has precisely the same action, now regarded as a map between sets of vertices and edges of graphs.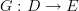 two functors, i.e. two morphisms in the category of categories, we have the relation
two functors, i.e. two morphisms in the category of categories, we have the relation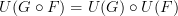
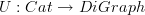 is indeed a functor.
is indeed a functor.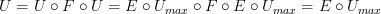
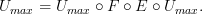
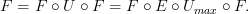
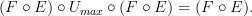
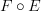 is the left adjoint of
is the left adjoint of 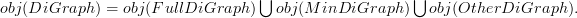
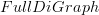 is a
is a 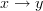 and
and 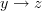 are directed edges, then
are directed edges, then  is also a directed edge.
is also a directed edge.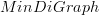 is a full subcategory of
is a full subcategory of 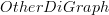 is a full subcategory of
is a full subcategory of 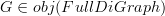 ,
, 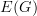 is the corresponding minimal digraph
is the corresponding minimal digraph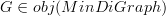 ,
, 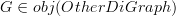 ,
, 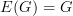
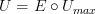
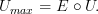
 is the same as what we call
is the same as what we call 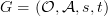 does not necessarily include all composite edges. For example, if
does not necessarily include all composite edges. For example, if 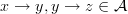 , then it is not necessary that
, then it is not necessary that 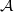 . Therefore, generally speaking,
. Therefore, generally speaking, 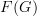 is not necessarily a category as described. To make sure that
is not necessarily a category as described. To make sure that 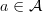 and then ALSO add morphisms to fill in the missing composites. Unless I'm overlooking something, this last step appears to be missing from the notes.
and then ALSO add morphisms to fill in the missing composites. Unless I'm overlooking something, this last step appears to be missing from the notes.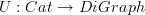 is the usual forgetful functor.
is the usual forgetful functor.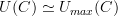 for any category
for any category 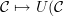 . Note the arrow that I've used here.
. Note the arrow that I've used here. ,
, 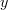 , and
, and  and three non-identity morphisms
and three non-identity morphisms