So you are thinking of this sentence of Tao's, here:
I believe that there is some equivalent way to axiomatise topology via continuous functions using the machinery of sheaves, which is in some ways more "natural" than the simple but somewhat arbitrary-looking axioms for open sets,
?
This does not mention sheaves on 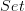 . Did he say something about that elsewhere?
. Did he say something about that elsewhere?
Yes, so my impression, too, is that he is simply referring to the sheaf topos on the category of open subsets of a topological space.
But there are of course ways to speak of topologies that are very category-theoretic and don't look like the ordinary definition. For instance a topology on a space is a sub-quantale of the power-set quantale or something like that. (I forget. Maybe sub-*-quantale).
But I think the royal road to topological spaces in terms of just category theory is regarding them as localic toposes. We can say "localic topos" using only very natural category-theoretic language that never looks ad hoc.
]]>