It should be true that when 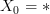 that the decalage
that the decalage 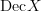 of
of 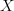 is the pullback along
is the pullback along 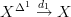 of
of 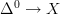 . Do we have a discussion of this in the literature anywhere?
. Do we have a discussion of this in the literature anywhere?
[ edit: this is of course not true: the decalage gives a smaller model for $X^I \times_X X_0$ ]
]]>There appears to be a typo in the section ’Morphisms out of the décalage’ in the line starting with ’the vertical morphism is given in degree by…’: should be replaced by .
]]>It feels like there ought to be a slick way to use décalage to produce a simplicial model for the relation , for any -group (simplicial group) . But if so, I don’t see it yet. Does anyone know?
]]>I moved the example of simplicial classifying spaces from the last paragraph of the Idea-section to a first subsection of the Examples-section (now here).
Incidentally, it used to say (and still says):
A central application is the special case where is the simplicial classifying space of a simplicial group (see at simplicial principal bundle). In this case , called , is a standard model for the universal simplicial principal bundle.
But that seems wrong to me, if we stick to standard conventions. I have added this followup remark:
]]>Or rather, with the conventions used at simplicial classifying spaces (which are those of Goerss & Jardine, p. 269) we have (shifting and forgetting the first, i.e. 0th, face-and degeneracy maps.)
[ old stupid remark removed ]
]]>beware, which 'internal hom'. The join is the tensor ofor an internal hom on augmented sSet, but this is not thee same as the usual internal hom, so 'an internal hom' would be safer wording.
]]>Edit:
@Urs: Yes, you actually can describe it that way. In Ehlers's thesis, he defines the internal hom in terms of the Décalage, because the latter is easier to describe explicitly.
]]>I added a query box to decalage on this point
]]>It should be true that when 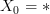 that the decalage
that the decalage 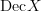 of
of 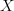 is the pullback along
is the pullback along 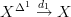 of
of 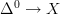 . Do we have a discussion of this in the literature anywhere?
. Do we have a discussion of this in the literature anywhere?
[ edit: this is of course not true: the decalage gives a smaller model for $X^I \times_X X_0$ ]
]]>You should add the link to PJ Ehlers's thesis here as well, which discusses all of this in detail (and has become pretty much my standard source for all of this simplicial homotopy theory ) stuff.
]]>It certainly is a Kan fibration if Kis a simplicial group since it is clearly an epimorphism.
In general, I think it is fairly easy to prove. IDEA: Suppose you have a (n,k) horn in Dec K so a sequence of faces with a gap. Map that down to K where you are given a filler for the horn and hence know the gap and what fills things there. The filler is a n+2 simplex in K so gives an n+1 simplex in Dec K. I think that will be the filler up top. There was a moment when I had some doubts about the compatibility with respect to the last face, but in fact you are GIVEN a filler for the horn down the bottom so I don't think now there is a problem.
Does that look right?
]]>edited decalage a bit
there was the statement that 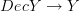 is a "fibration". I made that Kan fibration. Is that right?
is a "fibration". I made that Kan fibration. Is that right?