Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology definitions deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nforum nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: simplicial complex

Bottom of Page

1 to 40 of 40

  1.  
    • CommentRowNumber1.
    • CommentAuthorTodd_Trimble
    • CommentTimeApr 11th 2010
    • (edited Apr 11th 2010)

    Made some edits and additions at simplicial complex.

    • CommentRowNumber2.
    • CommentAuthorHarry Gindi
    • CommentTimeApr 12th 2010

    Lol =o

    Indeed, simplicial sets are essentially presheaves on the category of finite nonempty totally ordered sets

    Groups are essentially sets with a binary operation GxG->G that satisfies associativity, inverses, and identity. =)

    Yes, I'm making fun of your wording. =p

    • CommentRowNumber3.
    • CommentAuthorDavidRoberts
    • CommentTimeApr 12th 2010
    • (edited Apr 12th 2010)

    Well simplicial sets are defined as presheaves on 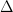\Delta (duh), but 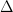\Delta is equivalent to the category of finite nonempty totally ordered sets, so these two presheaf categories are equivalent. I presume this is what the wording is meant to imply.

    • CommentRowNumber4.
    • CommentAuthorTodd_Trimble
    • CommentTimeApr 12th 2010

    I think you’ve missed the point!

    Notice that simplicial sets are defined to be presheaves on the category of ordinals and order-preserving maps. But here I’m taking presheaves on the category of all finite nonempty totally ordered sets. The category of simplicial sets is therefore equivalent to that presheaf category. The function of the word “essentially” is to indicate “up to equivalence”.

    • CommentRowNumber5.
    • CommentAuthorTodd_Trimble
    • CommentTimeApr 12th 2010

    (David, I guess it was clear I was writing to Harry.)

    • CommentRowNumber6.
    • CommentAuthorDavidRoberts
    • CommentTimeApr 12th 2010

    snap!

    • CommentRowNumber7.
    • CommentAuthorHarry Gindi
    • CommentTimeApr 12th 2010
    • (edited Apr 12th 2010)

    I've seen it defined literally as Psh(FinNonemptyLinearlyOrderedSets) (not using that silly notation of course) in the appendix of Lurie's book, if I remember correctly. I believe that this is the primary definition he gives, but he then notes that it is sufficient to work with the skeleton.

    • CommentRowNumber8.
    • CommentAuthorTodd_Trimble
    • CommentTimeApr 12th 2010

    Well, that’s Lurie then. Just about everybody else in the world defines it the way I just did; it’s the standard definition, as you can verify by looking it up in any textbook. Hence my “essentially” is entirely justified. However, I’ve updated the page (with a bit more material), and included something brief on “up to equivalence”.

    • CommentRowNumber9.
    • CommentAuthorHarry Gindi
    • CommentTimeApr 12th 2010
    • (edited Apr 12th 2010)

    Okay, I was a little quick to call you out on your wording and I apologize and concede. =)

    I like to think that my comment was at least funny though.

    • CommentRowNumber10.
    • CommentAuthorUrs
    • CommentTimeApr 13th 2010

    Why does simplicial complex cite “Convenieent categories of smooth spaces”?

    I have atl least moved the Spanier-reference before that.

    • CommentRowNumber11.
    • CommentAuthorTodd_Trimble
    • CommentTimeApr 13th 2010

    Because that’s where Baez and Hoffnung showed that simplicial complexes form a quasitopos of concrete sheaves (this is mentioned in the article). This result was certainly new to me; if there is another reference for it I should be glad to hear it.

    • CommentRowNumber12.
    • CommentAuthorUrs
    • CommentTimeApr 13th 2010

    Good, so I added that information here.

    • CommentRowNumber13.
    • CommentAuthorTim_Porter
    • CommentTimeDec 2nd 2010

    I have returned to simplicial complex and fixed some typos in it and some related entries. I am hoping to be able to clear up in my mind some of the confusion (again in my mind :-)) about the rigidified etale topological type that Friedlander defined. (Using pointed hypercoverings has always seemed to me to be inelegant and I think that there should be a neat (and also very explicit) treatment of a rigidified h.c. version of the Artin-Mazur construction, ending not in pro(H) but in a h.c. version of pro(SSet). I think this gives a h.c. representative of the functor given somewhere in the Lab of the shape of a topos.

    • CommentRowNumber14.
    • CommentAuthorTodd_Trimble
    • CommentTimeDec 2nd 2010

    Tim, I’ve seen references to this Artin-Mazur construction. What is it, please? Also, do you have an idea what this cryptic passage from the Esquisse means?:

    True, there is foundational work to be done here too, especially around the very notion of the tubular neighborhood of a subtopos – and it is actually surprising that this work (as far as I know) has still never been done, i.e. that no one (since the context of etale topology appeared, more than twenty years ago) apparently ever felt the need for it, surely a sign that the understanding of the topological structure of schemes has not made much progress since the work of Artin-Mazur…

    • CommentRowNumber15.
    • CommentAuthorTim_Porter
    • CommentTimeDec 2nd 2010
    • (edited Dec 2nd 2010)

    SLN100 is the short answer. It is the way they define the etale homotopy type of scheme. It results in a pro-object in the homotopy category. The homotopy progroups of this are the profinite completion of the standard homotopy if the scheme is nice enough and over the complex field. There was work done on tubular neighbourhoods in this context by David Cox. (I have some of his papers Ill. J. Math. if I remember rightly.)

    Eric Friedlander did a lot of work on this and then it got taken up by Quillen and Sullivan and eventually lead to the proof of the Adam’s conjecture. There is some mention of it in recent papers by Pridham, and Quick. (If anyone is interested I can provide chapter and verse as I am working with those documents to improve parts of the profinite algebraic homotopy monograph that I have been working on since 1984! :-))

    I must look back at Esquisses.. You will note that I have been revisiting the whole area with amendments and additions to the entry on Grothendieck. I ’really’ need to write something on ’Dessins d’enfants’ etc. for the lab and alos for the monograph, and then there is all the anabelian stuff as well…. heigh-ho.

    I also have to prepare a talk for later this month at the WIMCS meeting in Cardiff, and to think about the meeting in Lisbon in February… and I am supposed to be retired!!!!

    • CommentRowNumber16.
    • CommentAuthorUrs
    • CommentTimeDec 2nd 2010
    • (edited Dec 2nd 2010)

    I haven’t looked at the original source but know Artin-Mazur through the review in ieke Moerdijk’s Classifying spaces and classifying topoi . It was reading this that made me understand that in the locally contractible situation computing the homotopy groups of an object in a topos Sh(C)Sh(C) is the same as applying the left adjoint Π\Pi of the constant ∞\infty-stack functor of the corresponding ∞\infty-topos to that object.

    This revisionist review of Ieke’s review of Artin-Mazur/Johnstone/etc. is in the section in terms of local contractions in the entry on geometric homotopy groups in an ∞\infty-topos.

    • CommentRowNumber17.
    • CommentAuthorTim_Porter
    • CommentTimeDec 2nd 2010
    • (edited Dec 2nd 2010)

    @Urs Thanks for that link as it was that that I was looking at yesterday. I think my point in doing this is to make sure that we are ’backfilling’ the theory, linking up things with their origins, as there are useful constructions back there that could be easily forgotten as the theory goes forward and also certain insights and questions that are back there which give some good points to see how they look from the nPOV.

    I am also interested in seeing what I did back in the 1980s and 90s from the present viewpoint, and vice versa. Somehow I think that there are lots of ideas that link into the older insights that can be clarified, generalised and applied back having been examined in the ’modern’ light. That quote that Todd gives is a case in point I think. it would be nice to have an impact on other areas!!!

    (I feel sometimes that the lines of communication of the advance are quite thin and therefore ’vulnerable’… although in what way I am not sure.)

    • CommentRowNumber18.
    • CommentAuthorUrs
    • CommentTimeDec 2nd 2010

    Thanks for that link as it was that that I was looking at yesterday. I think my point in doing this …

    Tim, this sounds as if you feel you need to justify anything. But my comment above that parts of the Artin-Mazur story is indicated in the nLab entry on homotopy groups in an oo-topos was only meant as an information for Todd, who asked for details. I didn’t mean to imply anything by that. I certainly don’t think that the discussion there is in any way exhaustive and the final word. I don’t even claim that the discussion there is good. I am just saying that this little bit of discussion of Artin-Mazur does exist on the nLab. For whatever that’s worth.

    • CommentRowNumber19.
    • CommentAuthorTim_Porter
    • CommentTimeDec 2nd 2010

    Don’t worry. I took your comment in the way you intended it. As with everyone here, I sometimes write down my thoughts to justify TO MYSELF what I am trying to do. That reader is very picky!!! It also acts as a reminder on what ideas to follow up (e.g. I had completely forgotten about the tubular neighourhood idea in Esquise until Todd mentioned it. Now there will be a hint to myself to follow it up if I can. I have mislaid my hardcopy of Esquise (an original!) so have to rely on the version on my screen.)

    • CommentRowNumber20.
    • CommentAuthorColin Tan
    • CommentTimeMay 14th 2014

    It seems that being a simplicial complex is a property of a set graded over the natural numbers. Formally, the functor from the category of simplicial complexes to the category of sets graded over the natural numbers which sends a simplicial complex K to the graded set whose degree d elements are the d-simplexes of K is fully faithful, thus forgets only properties.

    This leads me to redefine a simplicial complex as a set K graded over the natural numbers such that each K dK_d is a subset of (K 0d+1)\binom{K_0}{d+1} and, for finite subsets x and y of K 0K_0 where y contains x and y belongs to K, then x belongs to K. Here (K 0d+1)\binom{K_0}{d+1} is a quotient set of a subset of the product K 0 d+1K_0^{d+1} where equivalence classes biject with (d+1)-element subsets of K 0K_0 (I learnt this notation from graph.) With this redefinition, a morphism of simplicial complex is a morphism of their underlying graded sets, in accord with the forgetting property yoga.

    • CommentRowNumber21.
    • CommentAuthorZhen Lin
    • CommentTimeMay 14th 2014

    Your claim cannot be correct. Consider the 1-simplex. It only has a trivial automorphism, but it has two points, so the underlying graded set has a non-trivial automorphism.

    • CommentRowNumber22.
    • CommentAuthorColin Tan
    • CommentTimeMay 14th 2014
    I don't understand. "Reflection" should be a simplicial complex automorphism of the 1-simplex. In detail, if we label the two vertexes of the 1-simplex by p and q, then swapping p and q is a simplicial complex (auto)morphism.
    • CommentRowNumber23.
    • CommentAuthorTim_Porter
    • CommentTimeMay 14th 2014
    • (edited May 14th 2014)

    I think the following is true: The set of vertices of the simplicial complex version of the 1-simplex is {0,1}\{0,1\}. The only 1-simplex is the whole set and there are two 0-simplices, {0}\{0\} and {1}\{1\}. That is all. There is a ℤ 2\mathbb{Z}_2-action in this description. The simplicial set 1-simplex has no non-trivial automorphism.

    Colin: your description seems very much more complicated than the classical one.

    (Edit: Colin we cross posted! You noticed the same thing.)

    • CommentRowNumber24.
    • CommentAuthorColin Tan
    • CommentTimeMay 14th 2014
    Hi Tim: possibly my description is more complicated. Given that we consider an object of a category the "same" as its image under a categorially equivalent functor, my description is the "same" as the usual description.
    • CommentRowNumber25.
    • CommentAuthorTodd_Trimble
    • CommentTimeMay 14th 2014
    • (edited May 14th 2014)

    Still, the claim that this functor is full seems fishy to me. Suppose for example we take the 3-simplex σ 3\sigma_3. The number of simplicial complex endomaps is bounded above by the number of maps on the set of 0-simplices, which is 4 44^4. On the other hand, the number of 1-simplices is 66, and this component of the graded set has 6 66^6 endomorphisms. Thus the composite map

    SimpComplex→jSet ℕ→ev 1SetSimpComplex \stackrel{j}{\to} Set^{\mathbb{N}} \stackrel{ev_1}{\to} Set

    cannot be full, and therefore neither can Colin’s functor jj be full.

    • CommentRowNumber26.
    • CommentAuthorColin Tan
    • CommentTimeMay 14th 2014
    Thank you Todd. You are right that j is not full. So all I have is that j is faithful, which means that being a simplicial complex is a structure on a set graded over the natural numbers.

    After a second look, I agree with Tim that my description j is complicated. How can I simplify this description j?
    • CommentRowNumber27.
    • CommentAuthorTim_Porter
    • CommentTimeMay 14th 2014

    Colin, why not look at partially ordered sets for some ideas? The poset of simplices of a simplicial complex is a good place to start. Of course, then the nerve / flag complex of that is the barycentric subdivision of the original. This does not get you back where you started but almost does. What do you want your other description for? That may give us some idea as to how to tweek it in a good direction.

    • CommentRowNumber28.
    • CommentAuthorColin Tan
    • CommentTimeMay 15th 2014

    Yes, thank you Tim for your suggesting to start with the poset of simplexes of a simplicial complex. I wish to understand the manner in which a simplicial complex is a CW complex with extra structure. Aware of debates including the one at this forum of which is a morphism between CW complex, let me suppose for now that a CW complex morphism is a cellular map. With this supposition, the geometric realization functor from the category of simplicial complexes to the category of CW complexes is fully faithful. Thus a being a simplicial complex is a property of a CW complex.

    I began with the ℕ{\mathbb{N}}-graded set description in imitation of the skeleton filtration of a CW complex, whose preservation is required for a map between CW complexes to be cellular. Your idea of starting with the poset of simplexes of a simplicial complex is beautiful, in the sense that I can begin to analyze how flags control the geometry of simplicial complex morphisms. The poset of simplexes of a simplicial complex is graded by dimension and a simplicial complex morphism preserves this grading and thus preserves flags. To what extent is a simplicial complex morphism a graded poset morphism with extra structure?

    I will analyze and understand the geometric situation in more detail.

  29. Over at simplicial complex, I streamlined the example of simple graphs as 1-dimensional simplicial complexes by pointing to the relevant discussion at graph, since it was discussed in more detail over there. I have a question about a parenthetical remark that was (is) attached to this example:

    (The case of a ‘multigraph’ where there can be multiple edges between vertices, and perhaps loops at a vertex, does not correspond to a simplicial complex, but does give a simplicial set.)

    It looks like this was originally written by Tim Porter: Tim, what specific construction were you referring to? I’m guessing you probably had in mind the representation of an undirected (multi)graph as a symmetric directed graph, hence as a 1-dimensional simplicial set equipped with an involution on 1-simplices (after formally adding identity edges at every vertex). If so, I could try to add a bit of text to elaborate (right here, and/or over at simplicial set and/or graph).

    • CommentRowNumber30.
    • CommentAuthorTim_Porter
    • CommentTimeAug 23rd 2017

    My thought was just that a 1-simplex in a (directed) loop can not be directly described by a simplicial complex as the only simplicial complex on a single vertex has just one simplex whilst the loop has two, Doh! Nothing complicated.

  31. Just to clarify, though, a 1-dimensional simplicial set is essentially the same thing as a directed graph (i.e., a quiver), so what exactly did you mean in referring to “multigraphs” (= undirected graph with loops and/or multiple edges)? On the one hand, a multigraph can be seen as a quiver equipped with an involution, and on the other hand, a quiver can be seen as an orientation of a multigraph – did you have either of these views in mind?

    • CommentRowNumber32.
    • CommentAuthorTim_Porter
    • CommentTimeAug 23rd 2017

    For me at that time ’multigraph’ was a ’graph’ with multiple (directed) edges allowed from any given source to any given target vertex. (As ’directed graph’= ’quiver’, perhaps ’multi-quiver’ might be a good term! )

  33. Ah, yes, that was the third possible interpretation I thought you might have had in mind. :-) Assuming it’s okay, I will go ahead and replace “multigraph” by something less ambiguous (“arbitrary directed graph (loops and multiple edges allowed)”), and also add this example to simplicial set.

    • CommentRowNumber34.
    • CommentAuthorTim_Porter
    • CommentTimeAug 23rd 2017

    That sounds fine.

  35. This link no longer exists: Kenny Erleben, Simplicial complexes (2010) (pdf slides)

    The slides can be found on course hero (https://www.coursehero.com/file/13538100/Notes-on-simplicial-complexes/) but that’s not a reliable source.

    story645

    diff, v42, current

    • CommentRowNumber36.
    • CommentAuthorUrs
    • CommentTimeAug 3rd 2021

    Thanks for the alert, but you should not have removed the reference item (as it seems you did in v 42) – unless there is a reason beyond the link being broken?

    I have re-instantiated the item (here) with a link recovered from the Wayback archive.

    diff, v43, current

    • CommentRowNumber37.
    • CommentAuthorDavid_Corfield
    • CommentTimeSep 25th 2021

    Added a reference

    • Maximilian Doré, Samson Abramsky, Towards Simplicial Complexes in Homotopy Type Theory (pdf)

    diff, v44, current

  38. The title of the talk is misleading, actually not relevant for this article.

    Maximilian Dore

    diff, v45, current

  39. The spheres obviously admit a PL structure, so I changed the wording. In fact, for n > 4 this PL structure is unique, I think, because the h-cobordism theorem goes through as in the top case by coning off, but I couldn’t quickly confirm by googling, so left it as “any PL structure”.

    Added an example where PL structure doesn’t exist.

    Mathquest

    diff, v46, current

    • CommentRowNumber40.
    • CommentAuthorUrs
    • CommentTime4 days ago

    added pointer to:

    diff, v47, current

1 to 40 of 40

  1.