nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorEric
- CommentTimeApr 27th 2010
I started an idea section at transgression, but it could probably use some going over by an expert. I hope I didn’t mess things up too badly. I was reading Urs’ note on “integration without integration” on the train ride home and fooled myself into thinking I understood something.
By the way, this reminded me of a discussion we had a while back
-
- CommentRowNumber2.
- CommentAuthorzskoda
- CommentTimeApr 27th 2010
There are several closely related notions of transgression, and Urs means just a particular one. Topologists often think of trasngression for spectral sequences, going back to papers of Borel and Serre, and corresponding relations between different cohomologies; Urs looks at the more fundamental level of mapping spaces, but in some situation it is not clear to me how to reduce to Urs’s case.
-
- CommentRowNumber3.
- CommentAuthorHarry Gindi
- CommentTimeApr 27th 2010
I made some edits to fix things some things so they look better and clarified what I could, but for example, there is not yet a definition of what a transgression is. I also dropped a comment box about exactly which loop space you were talking about (since there is the space of continuous loops and the space of smooth loops, both of which make sense).
-
- CommentRowNumber4.
- CommentAuthorEric
- CommentTimeApr 28th 2010
- (edited Apr 28th 2010)
My understanding is still superficial, but the reference I read prior to posting that was Urs’ Integration without Integration. This idea is also discussed at
An Exercise in Groupoidification: The Path Integral
I could be mistaken, but I think the idea is also a key component of Urs and Domenico’s recent discussion.
Also here:
- The First Part of the Story of Quantizing by Pushing to a Point…, n-Cafe
I think I see conceptually how the idea works. I think this is what is meant by the slogan, “integration by pushing to a point”.
For any parameter space and any target space , you look at the space of maps . I would be tempted to call this space “-space”, i.e. each point in -space corresponds to a map .
I would also be tempted to call -space “loop space”, but I noticed at loop space, it talks about pointed loops. Why is that? And if you are talking about maps from pointed loops, why not call it “pointed loop space” and leave “loop space” for the obvious space of maps ? No big deal. Just curious.
Anyway, I don’t have any answer for your question Harry. I know what I wrote was vague and in need of some attention. I hope someone can help. I’m no expert.
But this made me think of Froelicher space. I guess you want the space of maps from one space to another space to itself be a well defined space somehow.
You can tell from the first link above to the String Coffee Table, my understanding hasn’t improved too much in the last 6 years :)
From the future: Thanks David (comment #5). I’ve removed the offending comment about “corresponds to the image”. I hope that is alright.
-
- CommentRowNumber5.
- CommentAuthorDavidRoberts
- CommentTimeApr 28th 2010
corresponds to the image of in
no, because the map may not be injective, and all sorts of other reasons (and may even be constant at a point). Consider the maps given by and . These have the same image, and are injective, but are certainly not the same map.
There are two different sorts of loop spaces: free loop spaces (all maps ) and based loop spaces of a pointed space . Most often the is left off, with the basepoint being implicit. I guess when it says pointed loops it means based loops, but both are the loop space object in the category of pointed spaces and maps preserving the basepoint. This is before we get to the issue of smooth or continuous loops, but if you want to work with manifolds (as manifolds, with differential forms etc) then you need smooth loops. Then Andrew’s work on constructing smooth-type structures on loop spaces comes in handy (Frechet manifolds, Froelicher spaces, Chen spaces etc)
-
- CommentRowNumber6.
- CommentAuthorEric
- CommentTimeApr 28th 2010
- (edited Apr 28th 2010)
Hiding :)
-
- CommentRowNumber7.
- CommentAuthorDavidRoberts
- CommentTimeApr 28th 2010
- (edited Apr 28th 2010)
:D
-
- CommentRowNumber8.
- CommentAuthorDavidRoberts
- CommentTimeApr 28th 2010
- (edited Apr 28th 2010)
:D
-
- CommentRowNumber9.
- CommentAuthorEric
- CommentTimeApr 28th 2010
- (edited Apr 28th 2010)
David, would you mind if I change my original comment and remove the “corresponds to” and then we “hide” the subsequent comments?
In other words, can we play with the spacetime continuum? We can keep your comment #5, then I’ll reply. “Ok. Thanks! I’ve changed it.” :)
-
- CommentRowNumber10.
- CommentAuthorDavidRoberts
- CommentTimeApr 28th 2010
- (edited Apr 28th 2010)
:D
-
- CommentRowNumber11.
- CommentAuthorEric
- CommentTimeApr 28th 2010
Cool. Can someone with admin powers please hide comments #6 - #10 above and this comment?
-
- CommentRowNumber12.
- CommentAuthorDavidRoberts
- CommentTimeApr 28th 2010
Comment at transgression about LM, its notation and definition.
-
- CommentRowNumber13.
- CommentAuthorHarry Gindi
- CommentTimeApr 28th 2010
- (edited Apr 28th 2010)
Then we should say the "smooth free loop space" instead of just the loop space. Presumably it is still
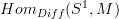 , but I don't know for sure.
, but I don't know for sure. -
- CommentRowNumber14.
- CommentAuthorUrs
- CommentTimeApr 28th 2010
- (edited Apr 28th 2010)
Great that you are discussing this. I hope to join you at some point, but right now I feel too busy with other things.
As a quick remark: what I hve said elsewhere about transgression applies to generalized smooth setups. In full generality: if you are in the oo-topos of oo-Lie groupoids and is a differential cocycle on some object , representing an -gerbe with connection on , then the image of that under the internal hom-functor is the trangression of that to an -gerbe with connection on the (free/based) loop space object of .
This is described in detail for the transgression of gerbes/2-bundles to bundles on loop space in my article with Konrad Waldorf on connections on gerbes. Concretely there then the loop spaces are regarded as diffeological spaces.
Konrad’s most recent articles are also about further details on this, though not forumlated quite as functorially. He is announcing a further followup that makes the relation to the functorial description manifest again.
I think it is a beautiful example of how the nPOV serves to conceptually almost trivialize a concept, because what could conceptually be more compelling than the internal hom, if it exists. And as Eric points out, it looks like this kind of mechanism should be a key input in an nPOV descritpion of quantization. However, unfortunately that last claim while seemingly and tantalizingly almost clear, still eludes me in some of its details.
-
- CommentRowNumber15.
- CommentAuthorEric
- CommentTimeApr 28th 2010
- (edited Apr 28th 2010)
However, unfortunately that last claim while seemingly and tantalizingly almost clear, still eludes me in some of its details.
That is only because you underestimate the value of progress made on discrete models. If nature is fundamentally discrete, then you’re basically done :)
-
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeApr 28th 2010
If nature is fundamentally discrete, then you’re basically done
Unfortunately not. I am still not quite sure about some aspects of the general abstract machinery that models “quantization”. Once it exists, it will work for discrete setups just as well as for non-discrete ones.
-
- CommentRowNumber17.
- CommentAuthorEric
- CommentTimeApr 28th 2010
- (edited Apr 28th 2010)
Oh good :) I thought all the fun was over with. Maybe I can help contribute something after all :)
In the end, it MUST be simple to be beautiful and I believe the answer will be beautiful. (I know I’m dreaming)
-
- CommentRowNumber18.
- CommentAuthorHarry Gindi
- CommentTimeApr 28th 2010
In the end, it MUST be simple to be beautiful and I believe the answer will be beautiful. (I know I'm dreaming)
There are lots of very deep theorems (for example, Zariski's main theorem) for which one cannot expect an easy proof.
Zariski's main theorem in commutative algebra says something stunningly powerful with only a few hypotheses, and there is no way to simplify it with category theory. At the core of differential geometry is solving differential equations locally. Similarly, at the core of algebraic geometry, you similarly have to solve commutative algebra problems locally.
Higher categories can't really help you much with that (although there are a few interesting applications of simplicial commuative rings, like the construction of the cotangent complex by André and Quillen (although Illusie constructed it without using simplicial methods)).
There are often abstract-nonsense ways of getting out of proving annoying things, but if you already incorporate category theory into your work, this isn't so surprising. However, I would argue that most deep theorems cannot be proven just by messing around with categorical language.
Things like extending the proof of excision from the simplicial homology case to the singular homology case is something that you would expect to be easy, and it is using category theory, but deep theorems like ZMT or Néron Desingularization, or reduction to characteristic p, or the structure theory for smooth, unramified, and étale morphisms are not things that just drop out for free when you have the right definitions.
-
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeApr 28th 2010
Right. I am not sure why we are discussing this now, but maybe with the emphasis on nPOV here it deserves to be highlighted:
The nPOV helps with getting the concepts straight and sorting out what exactly one should do or prove. One still has to go and do or prove it then! :-)
Here for instance the idea is: there are many and many technical definitions of what transgression is. The nPOV suggests a certain elegant unifying picture on these. But that doesn’t save one from doing explicit computations with these definitions.
But math is not just proving statements given certain definitions. The other half of math is finding the right definitions. That’s where the nPOV comes in.
-
- CommentRowNumber20.
- CommentAuthorHarry Gindi
- CommentTimeApr 28th 2010
The other half of math is finding the right definitions. That's where the nPOV comes in.
This is something that I agree with.
-
- CommentRowNumber21.
- CommentAuthorDavid_Corfield
- CommentTimeApr 28th 2010
To muddy the picture a little, there’s still a question of understanding when framing by the nPOV is likely to be powerful enough to point or to suggest a proof strategy, right down to the other end of the scale where we shouldn’t expect the nPOV to be of any help even in suggesting definitions, perhaps in, say, Ramsey theory. Do we find mathematics spread evenly over this scale? Can we expect things to change as the nPOV gains more of a hold? Might the nPOV change people’s perspectives on what kind of mathematics is worth pursuing?
-
- CommentRowNumber22.
- CommentAuthorAndrew Stacey
- CommentTimeApr 28th 2010
Started hacking transgression, not nearly done with the little that I know but have to stop for a bit.
@David: the phrase “compact-open” is about as ambiguous as “loop space”! does have “the compact-open topology”, but the interpretation of that for smooth maps includes information on all higher derivatives.
-
- CommentRowNumber23.
- CommentAuthorEric
- CommentTimeApr 28th 2010
- (edited Apr 28th 2010)
Andrew, is that the same transgression as what Urs talks about in Integration without Integration?
It seems vaguely similar, but not obviously the same as what I had in mind when I started writing the original “Idea” section.
-
- CommentRowNumber24.
- CommentAuthorAndrew Stacey
- CommentTimeApr 28th 2010
I’ll need to read that more carefully to be sure, but the phrase:
transgression consists of pullback followed by fiber [sic] integration.
gives me reason to believe that it is the same since “pullback and then integration” is exactly what I’m talking about over at transgression.
-
- CommentRowNumber25.
- CommentAuthorHarry Gindi
- CommentTimeApr 28th 2010
fiber [sic]
Fiber is a technically acceptable variant spelling (preferred in the US). It's like pediatrician and pædiatrician, color and colour, rigor and rigour, etc, so it doesn't deserve a "[sic]".
However, it is not related to "truck" and "lorry" or "restroom" and "loo", or anything daft like that.
-
- CommentRowNumber26.
- CommentAuthorUrs
- CommentTimeApr 28th 2010
Could you native speakers please be very specific and tell me explicitly whether I should better stick to “fibre” to be on the safe side, or whether it really doesn’t matter much? Thanks.
-
- CommentRowNumber27.
- CommentAuthorHarry Gindi
- CommentTimeApr 28th 2010
- (edited Apr 28th 2010)
According to my very unscientific google searches for "fiber bundle" and "fibre bundle", the first has roughly two and a half times as many hits, so I think that it's safe to say "fiber". It doesn't really matter which one you use, so I say use whichever one you prefer.
Remember, Andrew is from England, so he's biased.
-
- CommentRowNumber28.
- CommentAuthorUrs
- CommentTimeApr 28th 2010
- (edited Apr 28th 2010)
I added to transgression
a remark on how transgression to mapping spaces is an example
the missing links to generalized cohomology theory, to fiber integration and to Pontrjagin-Thom collaps map.
a toc
-
- CommentRowNumber29.
- CommentAuthorUrs
- CommentTimeApr 28th 2010
- (edited Apr 28th 2010)
To Eric:
what I have been talking about, elsewhere and here with Domenico, is how the special case of transgression to mapping spaces can be understood as being essentially just the internal hom, if cohomology is understood as described at cohomology. I should expand on that. But I don’t have time now!
-
- CommentRowNumber30.
- CommentAuthorAndrew Stacey
- CommentTimeApr 28th 2010
<blatant, but probably pathetic, attempt at a witticism><br/>”fiber” deserves a “[sic]” because only sic people write it like that<br/></blatant>
Okay, I apologise for the ’[sic]’: it was an attempt at being funny but clearly didn’t work. To make good my transgression, I shall continue with transgression.
-
- CommentRowNumber31.
- CommentAuthorTodd_Trimble
- CommentTimeApr 28th 2010
Regarding the thread exemplified in Urs’s # 19, I agree with him there, and I would add it also means finding the “right” statements.
First, Peter Freyd said something profound about category theory a long time ago: “Perhaps the purpose of categorical algebra is to show that which is trivial is trivially trivial.” In other words, one thing category theory does is help quickly to get to the heart of the matter, isolating the hard nuggets, which one may then attack with abandon.
Second, another thing it can do is change the form of the nugget. Grothendieck exemplifies this style; echoing his very poetic style of expression, he would speak of softening the hard matter by immersing it over time under a vast sea of theory, until it opens up naturally.
-
- CommentRowNumber32.
- CommentAuthorUrs
- CommentTimeApr 28th 2010
- (edited Apr 28th 2010)
Thanks, Todd. It would be nice if we could eventually have a paragraph with such nice comments over at nPOV. I regard that page as eventually supposed to become the page that transmits the nLab-spirit to the world.
-
- CommentRowNumber33.
- CommentAuthorTodd_Trimble
- CommentTimeApr 28th 2010
By the way, you will find Lab pages with both American and British spellings of the same word, depending on who is editing! In my opinion, that’s fine, and should be tolerated. There is a guideline we have that titles of pages should be spelled as in American English, but in the page itself, either way (or both ways!) is fine – there is no one “correct” way.
-
- CommentRowNumber34.
- CommentAuthorAndrew Stacey
- CommentTimeApr 28th 2010
(The spelling issue is off-topic, but just to emphazize: I agree with Todd. I wasn’t trying to make a point, I was trying to be funny. I promise not to do it again.)
-
- CommentRowNumber35.
- CommentAuthorUrs
- CommentTimeApr 28th 2010
I wasn’t trying to make a point, I was trying to be funny. I promise not to do it again.
No, that’s fine Andrew. You know, humour works if nobod feels insecure. Here it was me feeling insecure. That’s why I asked. But now I understand.
-
- CommentRowNumber36.
- CommentAuthorHarry Gindi
- CommentTimeApr 28th 2010
Second, another thing it can do is change the form of the nugget. Grothendieck exemplifies this style; echoing his very poetic style of expression, he would speak of softening the hard matter by immersing it over time under a vast sea of theory, until it opens up naturally.
This is true, but many many theorems in EGA and SGA have very difficult steps. For example, in Zariski's main theorem, you prove something like five reductions of the problem before the actual proof, but the actual proof is still hard.
-
- CommentRowNumber37.
- CommentAuthorAndrew Stacey
- CommentTimeApr 28th 2010
Back to transgression. I’ve added a fair bit, now. Certainly stylistically it needs work, but there’s a reasonable amount of content there now. I’m not sure what direction to take it in further. Several are possible that I know something about: further exposition on the iterated integrals, (Chens’ work, and the further developments by Jones, Getzler, and Petrack spring to mind, linking then to cyclic cohomology). Also, it would be good to relate this to transgression as is usually understood by algebraic topologists.
Moreover, as I hinted, it’s nowhere near polished. But as it’s the stuff I know, then I don’t know which bits are unclear to others.
Also, I’ve not been good at linking to other areas in the lab. I guess I ought to just double-bracket anything that I think might have a page, or ought to have a page, but I’m not in the habit of doing that yet.
-
- CommentRowNumber38.
- CommentAuthorTodd_Trimble
- CommentTimeApr 28th 2010
@Harry # 36, okay, and we could speak philosophically all day about this I guess (there is much more that could be added). But (and this is to everyone), in the meantime I have added, per Urs’s request, some summary statements over at nPOV.
-
- CommentRowNumber39.
- CommentAuthorAndrew Stacey
- CommentTimeApr 28th 2010
Incidentally, I’ve pretty much gotten rid of what was originally there. From what I could see, the maps went in the wrong directions. I’m not too clear on exactly what was meant, but from what I can tell (looking at revision 1), the first part looks like the relationship between the pullback in cohomology and the pushforward in homology. Thus if and then for we have .
The second part looks more like what I think of as transgression, but stuff ends up going in the wrong direction. I’m not sure whether or not it’s valuable to pick it apart to see where things start going wrong. In the simplest case, take a -form on . This is a function . The original statement said that this could be pulled back to a -form on . That is, a function (linear on fibres). I don’t see even how to start defining this -form without further conditions on .
It is certainly true that a function defines a function on closed -simplices in (err, modulo a few issues about smooth versus continuous), but unless is closed (and “closed” here is not precise as there are various interpretations that could be used which I don’t want to have to think about right now!) itself, this won’t descend to homology. So unless is very special, there’s no hope of a -form coming from it.
The other direction, however, is possible. Given a -form on we get a function simply by integrating round loops:
-
- CommentRowNumber40.
- CommentAuthorHarry Gindi
- CommentTimeApr 28th 2010
The original statement was about 0-forms on LM. Maps f:LM->R are precisely 0-forms!
-
- CommentRowNumber41.
- CommentAuthorAndrew Stacey
- CommentTimeApr 28th 2010
Not sure what you’re trying to say, Harry. Didn’t I just say precisely that?
There is a connection between -forms on and -forms on . This is that there is a map . My reading of the original content was based on this statement:
Now a 0-form α∈Ω 0(ℒℳ) “pulls back” to a 1-form ℒ *α∈Ω 1(ℳ)
(Memo to self: ask Jacques to extend the “source” view to all revisions)
which appears to be talking about a map , i.e. the wrong way around.
(Just noticed a rather appalling grammatical error near the end. Fortunately, Urs has edited the page since I last did so I can blame him for it.)
-
- CommentRowNumber42.
- CommentAuthorEric
- CommentTimeApr 28th 2010
Sorry about getting the direction wrong :|
I always think you want “pull back” forms and “push forward” domains. You can see, I got confused about the direction 6 years ago as well :)
So with transgression you “push forward” forms. Hmm…
Can we still salvage anything from:
? Transgression almost makes me want to write:
Of course you can’t always “push forward” a form, just like you cannot always transgress. Are the reasons related?
-
- CommentRowNumber43.
- CommentAuthorUrs
- CommentTimeApr 28th 2010
Thanks a lot, Andrew. Very nice! I promise to add something later – later this year ;-) – to try to bridge the gap between what Eric was seeing at the horizon and the stuff you put in there. For the moment I am just glad that somebody is taking care of that, as I am busy otherwise (as I might have mentioned).
But I added some links.
Also, I’ve not been good at linking to other areas in the lab. I guess I ought to just double-bracket anything that I think might have a page, or ought to have a page, but I’m not in the habit of doing that yet.
Yes, I was gonna ask you all about this: I keep going after you over your entries and add double brackets to about everything in sight. That’s because I am thinking one of the very strong points of the wiki is that it has the hyperlinks. You know, especially where we are encyclopedic, as we are here, i.e. where we reproduce material that is “in the literature”, the huge bonus of having that “well known” material on the wiki is and will be that here it is fully hyperlinked. Eventually, if we continue, young students will be able to move through material that back then took me, you, everybody, days or months to move through via libraries, Google searches and accidental lucky remarks overheard in the tea room. That’s why I feel like having hyperlinks all over the place. Ideally I think there should be a piece of software that simply checks every single word or phrase and hyperlinks it if it sees that there is a wiki entry on that.
As I mentioned before, I think if the typesetting of the hyperlinks is sufficiently low-key, this will not hurt the readability of the text. And if it does, then we hould adjust the appeaance of hyperlinks.
-
- CommentRowNumber44.
- CommentAuthorUrs
- CommentTimeApr 28th 2010
Todd, thanks for your paragraph at nPOV. Very nice!
-
- CommentRowNumber45.
- CommentAuthorDavid_Corfield
- CommentTimeApr 28th 2010
You don't suppose
Nothing in mathematics makes sense except in the light of higher category theory.
is a little strong? Perhaps it's meant as a deliberate exaggeration, although we could aways say that 0-categories are a part of higher category theory.
-
- CommentRowNumber46.
- CommentAuthorUrs
- CommentTimeApr 28th 2010
- (edited Apr 28th 2010)
If people feel it’s too strong, please remove it.
I found the statement to be a very good analog of the original statement in biology. And yes, I certainly think of ordinary category theory and 0-category theory as being included in higher category theory.
-
- CommentRowNumber47.
- CommentAuthorHarry Gindi
- CommentTimeApr 28th 2010
I made a new topic to continue this discussion since we're off on a tanget.
-
- CommentRowNumber48.
- CommentAuthorEric
- CommentTimeApr 29th 2010
Last night (while sleeping as usual), I was thinking about this, and had the idea maybe transgression can be thought of as pulling back a form, but I just had the original map going the wrong way. (Disclaimer: You probably noticed that I state things the way I current think about them, which is often incorrect, so statements like the previous one should be interpreted more as a question than a statement.)
Instead of pushing forward a loop to a point in loop space , maybe I wanted to push forward a point in loop space to a loop in . This map would “spray” a single point in to a bunch of point in , i.e. those that make up the loop, so pulling a form back from to would be “aggregating”, a.k.a. integrating. The adjoint of “spray” is “integrate” :)
Are there maps and ?
If so, then (I’m guessing) transgression is like pulling back along . Or something…
PS: Sorry, I know there is a very nice page on transgression now, but in the process of cleaning it up, you pushed it into a realm I can no longer easily understand.
-
- CommentRowNumber49.
- CommentAuthorHarry Gindi
- CommentTimeApr 29th 2010
There's no pushing forward a loop in M to a point in LM. This is the definition of LM (the loop space functor is representable, so this is trivial). I would assume that there is actually more going on there.
-
- CommentRowNumber50.
- CommentAuthorEric
- CommentTimeApr 29th 2010
- (edited Apr 29th 2010)
There’s no pushing forward a loop in M to a point in LM.
Yeah. This is where I went astray initially, but now I’m talking about the other way, i.e. pushing a point in to a loop in . That is what I meant by “spray” because a single point in gets sent to a continuum of points in . I think a map would send a point in to the image of in . Or something…
The idea is that we just relabel some stuff in the earlier standard expressions. Now and and we have
since , its integral is simply evaluation.
-
- CommentRowNumber51.
- CommentAuthorAndrew Stacey
- CommentTimeApr 29th 2010
@Eric: firstly, given that I added stuff to the transgression page sparked by your original stub, if there’s stuff you don’t understand then we should rewrite it so that you do understand it. However, not being able to see inside your head (!), I can’t tell which bits aren’t easy.
The conceptual problem I see in what you’ve just written is the distinction between a function (or “morphism” if we’re being good category theorists) and a relationship (I’m struggling to find a non-mathematically-loaded term here, I mean this without any mathematical meanings). Thus and are clearly closely related, but you have to be careful when trying to turn that casual relationship into an actual function. And if you want to do stuff like pullbacks and pushforwards then you do need actual functions.
So the statement “pushing a point in to a loop in ” is fine (though a bit awkward, I would prefer Harry’s “a point in is a loop in ”) when taking in general terms about the relationship between and : it’s a point that needs emphasising a lot when someone is starting to work with . But when expressed as a mathematical function, it’s a tedious old tautology: “a point in is a function ”.
A perhaps better example where the mathematical relationship is not quite a tautology is in the description of the tangent bundle of the loop space (this is on the transgression page, by the way). Here there are two ways of thinking of an infinitesimal deformation of a loop: either as a small deformation of the loop as a whole, or as a family of deformations of each point of the loop. In the first case, you are considering an element of and in the second of . The fact that these two are equivalent views of the same thing translates mathematically into an isomorphism and that is extremely useful.
To come back to what you said above:
I think a map would send a point in to the image of in .
to turn that “relationship” into a function, you need to look at the last bit: “to the image of in ”. From that, we can see that your function does not take values in , but in (the powerset of ), or perhaps some small family of subsets, and so your function is .
-
- CommentRowNumber52.
- CommentAuthorEric
- CommentTimeApr 29th 2010
Oh! Thanks Andrew.
However, not being able to see inside your head
Consider yourself lucky :)
I can’t tell which bits aren’t easy.
There probably are no bits that aren’t easy. There is a difference between what is easy and what I understand :)
Somewhere, years ago, I drew a figure for Urs on the tangent space of loop space. If we can find it, maybe we can include it on the nLab.
From that, we can see that your function does not take values in , but in (the powerset of ), or perhaps some small family of subsets, and so your function is .
Ah ha! Yes. Simple. What I was looking for was , i.e. the space of 1-chains on . So and this pushes forward to . I need to think about it, but that is probably closer to being actual maths.
-
- CommentRowNumber53.
- CommentAuthorEric
- CommentTimeApr 29th 2010
In Urs note on Integration without Integration, he’s got the expression
On the train home, I was trying to put the pieces in the right buckets, e.g. with
Then, if I write , then
Then I allowed myself to wander and wondered if I might want to be looking at
instead of
When I started thinking about , I wrote down
Is this correct? Is the space of 0-chains on the space of push forward maps ? That makes sense to me and would be kind of neat. Maybe even related to transgression :)
Another question, given , are there maps
and
? If that last map makes any sense, then this combined with my previous wanderings would mean
is actually a “generalized push forward” and the corresponding “generalized pull back”
is transgression.
Does any of that rambling make any sense?
-
- CommentRowNumber54.
- CommentAuthorEric
- CommentTimeApr 29th 2010
Sorry for rambling, but when just stared at
it made me wander if we could write
but then if that makes any sense, then we really want some kind of convolution
I’m getting groggy and better hit the sack before I ramble too much (Too late? :))
-
- CommentRowNumber55.
- CommentAuthorzskoda
- CommentTimeApr 30th 2010
I was thinking a bit on transgression in October, I mean the usual transgression in algebaric topology, in the subject of spectral sequences. It is of course related to the what you talk here. I wish I had time then to write that down, but did not, just a opne page at transgression (zoranskoda). It would be interesting on commenting on the connection.
-
- CommentRowNumber56.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 16th 2010
- (edited May 16th 2010)
it would be nice to have a neat nPOV description of transgression at least for loop spaces, where it should amount to a natural morphism
for any deloopable object . we should have it at least when is “nice topological spaces” (or, equivalently, oo-groupoids) and for an abelian group .
for topological spaces it should work as follows: given a topological space and an abelian group , the module of -cochains on with coefficients in is . An -simplex in is by definition a map , so it lifts to a map which, by a simplicial decomposition of gives an element in the -module . we therefore have a map of -modules for any . the map should be a map of complexes, and so taking homs into we should obtain the transgression map.
for oo-groupoids, one can read the above constructiona s follows: a functor is a rule telling us how to associate an -decoration with an -morphism in . to any -morphism in we can associate an -morphism in , so we get a rule telling us how to associate an an -decoration with an -morphism in . this rule turns out to be a functor .
a definition of the transgression map along these lines as well as an explicit simplicial decomposition of is (at least if I have not misunderstood) in Simon Willerton’s math/0503266. (if I’m not wrong the case where is a 1-groupoid and is treated there, but the argument seems to be quite general).
-
- CommentRowNumber57.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 16th 2010
what I wrote could be better said as follows: let be a compact closed -dimensional manifold (in the above post , but there is nothing special about this choice). then, for any nice topological space we have a map of complexes
A -cycle representing the fundamental class of gives a morphism of complexes and from this we get a morphism of complexes
taking homs into gives the integration over (the representing cycle for) map
if , then we have the evaluation map , and so the pull-back map . By composition we get the transgression map
-
- CommentRowNumber58.
- CommentAuthorUrs
- CommentTimeMay 16th 2010
- (edited May 16th 2010)
it would be nice to have a neat nPOV description of transgression at least for loop spaces
Yes. I thought about this when we discussedd the step where we use the universal coefficient theorem in the thread on DW theory.
We have the following statement in :
Let be an -groupoids and the fundamental -groupoid of a -dimensional manifold. Then forming the internal hom followed by -truncation gives a map
This is transgression in integral cohomology. As you pointed out, the same argument is true with replaced by an projective -module.
It would seem to me that this is the nice abstract argument, and that the chain complex computation that you point out is a specific realization of it.
-
- CommentRowNumber59.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 16th 2010
yes, I’m convinced. we should now collect all the pieces of this into the transgression entry. to late for doing it now. tomorrow..
by the way, injective -module.
-
- CommentRowNumber60.
- CommentAuthorUrs
- CommentTimeMay 16th 2010
Oh, injective, right.
Okay, if you could do that tomorrow, that would be nice.
-
- CommentRowNumber61.
- CommentAuthorUrs
- CommentTimeMay 16th 2010
Domenico,
I couldn’t stop myself and put in a brief remark at Transgression in terms of internal homs.
But I don’t quite have the time for this right now. Please expand and polish tomorrow. In case you have the time and feel like it, that is. :-)
-
- CommentRowNumber62.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 17th 2010
added a line to explain the role played by an orientation of . I think we could stress this and define an manifold to be -orientable if one has homotopy equivalences for any (which maybe reads more nicely as for any ), and to call it -oriented if a choice (or a choice up to homotopy) of these equivalences has been given.
then we could reduce the role of universal coefficients to a remark: if is an injective -module, then a -orientation determines a -orientation.
what do you think?
-
- CommentRowNumber63.
- CommentAuthorUrs
- CommentTimeMay 17th 2010
I think we could stress this and define an manifold to be -orientable if one has homotopy equivalences for any […] and to call it -oriented if a choice (or a choice up to homotopy) of these equivalences has been given.
Very interesting point. That would be nice, if that’s what going on.
Do you see a way to check that this relates to orientation in generalized cohomology and the way it is used in fiber integration generally?
-
- CommentRowNumber64.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 17th 2010
- (edited May 17th 2010)
not able to see a neat relation at the moment :-(
I’m trying to think to the most classical instance of this orientation stuff, namely: how do we get a top dimensional cohomology class on a compact oriented differential manifold? things should go as follows: let be an -dimensional differential manifold. then the tangent bundle of gives an element in . obstruction to orientability, i.e., to a lift to is the element in obtained by postcomposition of with . more precisely, a lift exists if and only if is in the connected component of the base point in . if obstruction vanishes (i.e., is in teh connected component of the base pointt, then (and this is the crucial point, and I am still missing it from abstract nonsense) a choice of a lift gives an element in . on the other hand, even if a lift does not exist, should define an element in .
in all this argument there must be something special about being the tangent bundle, but I am missing it :-(
-
- CommentRowNumber65.
- CommentAuthorUrs
- CommentTimeMay 17th 2010
In that argument involving the universal coefficient theorem over at Dijkgraaf-Witten theory: orientability of the manifold is a necessary assumption, I suppose?
-
- CommentRowNumber66.
- CommentAuthorzskoda
- CommentTimeMay 17th 2010
- (edited May 17th 2010)
Do you see a way to check that this relates to orientation in generalized cohomology and the way it is used in fiber integration generally?
Hence maybe to spectral sequences where transgressed elements are used in original paper of Borel (listed I think in transgression (zoranskoda).
-
- CommentRowNumber67.
- CommentAuthorzskoda
- CommentTimeMay 17th 2010
- (edited May 17th 2010)
Oh no, Borel’s reference is missing, I have to dig it out and put there.
Edit: I added it in transgression (zoranskoda), I mean the Ann. Math. 1953 reference. I created entry Armand Borel.
-
- CommentRowNumber68.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 17th 2010
- (edited May 17th 2010)
In that argument involving the universal coefficient theorem..
Yes. For a connected compact -dimensional manifold the following are equivalent:
is orientable;
.
(and, for the sake of completeness, in the nonorientable case one has ).
-
- CommentRowNumber69.
- CommentAuthorUrs
- CommentTimeMay 18th 2010
- (edited May 18th 2010)
Domenico,
with a student here, who is trying to understand the pull-push operations in string topology from a more abstract point of view, we were thinking about the following:
we here claimed so far to know how to do fiber integration in oo-topos-cohomology for trivial bundles:
for a trivial bundle object, we say the fiber integration map is
where the last step is postcomposition with the truncation and using the assumption that is “A-oriented” in the sense that we have been discussing.
Now: what about nontrivial but locally trivial fiber bundles? Can we generalize to that case?
I am thinking it should work as follows:
Let be the possibly nontrivial bundle, choose a cover over which it trivializes with typical fiber . We have
and I think
So then we can produce a map
Et voilà. :-)
(I try to give a clean account tomorrow, this just to record a thought. It’s too late now to follow up on more details.)
-
- CommentRowNumber70.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 18th 2010
- (edited May 18th 2010)
Et voilà. :-)
:-)
Yes, I agree. Great job!
as a first check, let us translate it into down to earth terms of usual integration of differential forms: we have a bundle with typical (compact, oriented) -dimensional fibre , a degree differential form on , and we want to make fibre integration. to achieve this, we cut in overlapping pieces such that on every piece the bundle trivializes ; then we fiber-integarte on each piece, getting degree differential forms on . now we only have to check that the ’s glue togheter, but this is assured by a simple commutative diagram involving fibre integration on the intersection , so have the result as soon as we:
i) have the diagram, i.e., realize as
ii) the diagram commutes, i.e. fibre integration for trivial bundles is functorial in the base (and this is obvious)
so I guess that yes, we have it!
-
- CommentRowNumber71.
- CommentAuthorUrs
- CommentTimeMay 18th 2010
- (edited May 18th 2010)
so I guess that yes, we have it!
One point maybe I still need to think about, which I found obvious yesterday but now think might require a bit more thinking:
my notation above is a bit abusive, in that it does not indicate how the hocolim acts on the fiber piece.
while in each degree, the simplicial object whose hocolim is looks like a -piece times , the face and degeneracy maps do act on of course.
Take the case of a -principal bundle and , classified by a transition function . Then the edges in that simplicial object are of the form
where and and subject to the relation that
So when in the formal computation that I posted above I throw over the -factor to the right and then take the colimit back into the hom to conclude that now it produces , there, I am secretly assuming the following:
that is invariant under the action of on itself by right multiplication.
Now, this is not out of the question. For instance it does hold in the concrete example that you just mentioned, with differential forms, where it just says that
as a consequence of the diffeomorphism invariance of the integral.
I bet this is true in full generality, so that the formula I gave is right, but right now I am lacking a formal proof of this invariance in full generality.
But let’s see: it should also be evident in the case of cohomology with coefficients in an injective -module , as in that case the argument, as you pointed out, only relies on the isomorphism given by the fundamental class, and that is invariant under diffeomorphisms, too.
So I suppose everything is fine. But it may still require some thinking.
-
- CommentRowNumber72.
- CommentAuthorDavidRoberts
- CommentTimeMay 18th 2010
- (edited May 18th 2010)
You should be able to calculate P as a coend, as in the traditional clutching construction. Let be the codiscrete groupoid on the index set of the cover. I’m guessing that
where is the constant functor with value the fibre . Doesn’t this give the homotopy colimit as in Domenico’s i) in #70? (Edit: Urs and I crossed over there, this was written after #70)
-
- CommentRowNumber73.
- CommentAuthorUrs
- CommentTimeMay 18th 2010
Ahm, wait, if is really constant then
That’s what I meant in my previous comment: the notation is a bit abusive, in that it does not indicate the action on the fiber.
-
- CommentRowNumber74.
- CommentAuthorDavidRoberts
- CommentTimeMay 18th 2010
Hmm. ok. Actually, the functor is constant on objects, but sends the arrow to an automorphism of . You know, I don’t think (and I was unsure at the time) that the coend is over . Maybe it should involve a functor where is the Cech groupoid of . Then the functor is really the composite \to Top$, the first being projection onto the index set, and the latter picking out the open set of the cover. We then use the coend
although I don’t know what it means to take a coend over a toplogical groupoid.
-
- CommentRowNumber75.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 18th 2010
I am secretly assuming that is invariant under the action of on itself by right multiplication
precisely. the secret assumption is that the homotopy equivalence is natural in ,i.e., that is a natural homotopy equivalence of functors .
-
- CommentRowNumber76.
- CommentAuthorUrs
- CommentTimeMay 18th 2010
Ahm, wait. I believe I was saying that it should even be invariant under .
The intuition is: the integral over an oriented manifold is invariant under oriented automorphisms of the manifold.
-
- CommentRowNumber77.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 18th 2010
exactly. the functor on the right in is the constant functor, so what I wrote was meant to be invariance. where am I wrong?
-
- CommentRowNumber78.
- CommentAuthorUrs
- CommentTimeMay 18th 2010
Oh, sorry, now I see I misunderstood you. Sorry. That’s of course exactly what you said!
-
- CommentRowNumber79.
- CommentAuthorUrs
- CommentTimeNov 9th 2010
I hav dug out an old article by Borel on transgression of differential forms through fiber bundles and added remarks on it at transgression and Chern-Simons element.
Search for “Borel” to see what i did
-
- CommentRowNumber80.
- CommentAuthorzskoda
- CommentTimeNov 10th 2010
That was the source which I started writing a year ago in transgression (zoranskoda) but stopped. I did not quite understand the connection with what you wrote and wrote to you about it, but we did not grasp the connection exactly at the time. The Borel’s case for fiber bundle was the motivation for the later generalizations for arbitrary spectral sequence setup. I am glad you returned to this and that things are getting clearer now. I still do not get it quite.
-
- CommentRowNumber81.
- CommentAuthorUrs
- CommentTimeNov 10th 2010
- (edited Nov 10th 2010)
I also seem to be lacking at least one step in the general story.
But one thing at least might be useful to note: Borel’s notion of transgression is really a special case of the connecting homomorphism for the long sequence in cohomology induced by the short sequence
and restricting to for a fiber bundle.
I have that remark already spelled out at Chern-Simons element. I’ll add it now very briefly also to transgression.
-
- CommentRowNumber82.
- CommentAuthornLab edit announcer
- CommentTimeDec 22nd 2020
-
- CommentRowNumber83.
- CommentAuthornLab edit announcer
- CommentTimeDec 22nd 2020
-
- CommentRowNumber84.
- CommentAuthorUrs
- CommentTimeJul 10th 2021
Added these pointers on transgression of group cohomology for discrete groups to cohomology of inertia groupoids:
Simon Willerton, Section 1 of: The twisted Drinfeld double of a finite group via gerbes and finite groupoids, Algebr. Geom. Topol. 8 (2008) 1419-1457 (arXiv:math/0503266)
Jean-Louis Tu, Ping Xu, Section 3 of: The ring structure for equivariant twisted K-theory, J. Reine Angew. Math. 635 (2009), 97–148 (arXiv:math/0604160, doi:10.1515/CRELLE.2009.077)
Alejandro Adem, Yongbin Ruan, Bin Zhang, Section 4 of: A Stringy Product on Twisted Orbifold K-theory, Morfismos (10th Anniversary Issue), Vol. 11, No 2 (2007), 33-64. (arXiv:math/0605534, Morfismos pdf)
-
- CommentRowNumber85.
- CommentAuthorUrs
- CommentTimeJul 10th 2021
I claim that the above formulas for transgression of group cocycles to inertia groupoids reflect the Eilenberg-Zilber formula for the degenerate simplices in the product of simplices, and that this relation is the way to actually prove that the formula expresses transgression. Obvious as that may be (?), none of the references I have seen really says this.
Is there a reference that does?
-
- CommentRowNumber86.
- CommentAuthorUrs
- CommentTimeJul 10th 2021
- (edited Jul 10th 2021)
What I mean is that the full proof of the transgression formula for group -cocycles to -cocycles on the inertia groupoid should be the following kind of computation – where “EZ” denotes the Eilenberg-Zilber map/theorem, which brings out the characteristic alternating sum-structure of the transgressed cocycles (and the other operations are the derived Dold-Kan equivalence, the derived internal hom-adjunction and the derived free/forgetful adjunction):
-
- CommentRowNumber87.
- CommentAuthorjim stasheff
- CommentTimeJan 14th 2022
The entry for transgression is very clear for the free loop space or the based loop space, but what about the path space PM \to MxM?
That seems very much related to Igusa's /t in his Iterated integrals -
- CommentRowNumber88.
- CommentAuthorUrs
- CommentTimeDec 9th 2022
- (edited Dec 9th 2022)
added more references which discuss transgression as pullback along the evaluation map followed by fiber integration over the domain space:
Jean-Luc Brylinski, §3.5 in Loop Spaces, Characteristic Classes, and Geometric Quantization, Birkhäuser (1993) [doi:10.1007/978-0-8176-4731-5]
Ernesto Lupercio, Bernardo Uribe, p. 2 in: Holonomy for Gerbes over Orbifolds, J. Geom.Phys. 56 (2006) 1534-1560 [arXiv:math/0307114, doi:10.1016/j.geomphys.2005.08.006]
Christian Bär, Christian Becker, Def. 9.1 in: Differential Characters and Geometric Chains, in: Differential Characters, Lecture Notes in Mathematics 2112 [arXiv:1303.6457, doi:10.1007/978-3-319-07034-6_1]
The last of these cites the first, the first two of these cite nobody for the concept. I guess people feel that this should be classical but don’t know an original reference.(?)
-
- CommentRowNumber89.
- CommentAuthorUrs
- CommentTimeDec 11th 2022
added the following pointers, and will copy them now also to a new entry fusion bundle:
Konrad Waldorf, Transgression to Loop Spaces and its Inverse, I: Diffeological Bundles and Fusion Maps, Cah. Topol. Geom. Differ. Categ., 2012, Vol. LIII, 162-210 [arXiv:0911.3212, cahierstgdc:LIII]
Konrad Waldorf, Transgression to Loop Spaces and its Inverse, II: Gerbes and Fusion Bundles with Connection, Asian Journal of Mathematics 20 1 (2016) 59-116 [arXiv:1004.0031, doi:10.4310/AJM.2016.v20.n1.a4]
Konrad Waldorf, Transgression to Loop Spaces and its Inverse, III: Gerbes and Thin Fusion Bundles, Advances in Mathematics 231 (2012) 3445-3472 [arXiv:1109.0480, doi:10.1016/j.aim.2012.08.016]
1 to 89 of 89