nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorMike Shulman
- CommentTimeMay 11th 2010
Added appropriate axioms for the various definitions of affine space, along with another definition in terms of a single quaternary operation.
-
- CommentRowNumber2.
- CommentAuthorHarry Gindi
- CommentTimeMay 11th 2010
- (edited May 11th 2010)
How is this definition of affine space related to the notion of an affine space in algebraic geometry (by which I mean
![\mathbb{A}^n_S:=Spec(\mathbb{Z}[x_1,\dots,x_n]) \times_\mathbb{Z} S \mathbb{A}^n_S:=Spec(\mathbb{Z}[x_1,\dots,x_n]) \times_\mathbb{Z} S](/extensions/vLaTeX/cache/latex_45540de050f16520a576fea22606031f.png) for an scheme (or algebraic space/stack?)
for an scheme (or algebraic space/stack?) 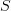 .)? It's obvious when
.)? It's obvious when 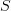 is the spectrum of an algebraically closed field, but not in more general cases.
is the spectrum of an algebraically closed field, but not in more general cases. -
- CommentRowNumber3.
- CommentAuthorDavidRoberts
- CommentTimeMay 11th 2010
- (edited May 11th 2010)
There is a bifurcation of meanings: affine spaces in alg. geom. are a generalisation (and relativisation) of a vector space to other base rings. Affine spaces in the sense at affine space are more of an algebraic abstraction of the structure that appears in Gallilean relativity (for example): a vector space with no origin. In other words, a torsor for the underlying abelian group of a vector space.
Edit: If is an affine scheme for some ring, then I imagine is related to the torsor for the underlying abelian group of somehow. For a more general scheme, I don’t know.
-
- CommentRowNumber4.
- CommentAuthorMike Shulman
- CommentTimeMay 11th 2010
If an affine space over R is defined to mean , then it’s a generalization of a vector space. But if it means a scheme isomorphic to without a specified isomorphism, then it’s a generalization of “a manifold isomorphic to ”. The meaning used here is for something in between – a space isomorphic to (or ), without a specified isomorphism, but with some additional structure remembered.
-
- CommentRowNumber5.
- CommentAuthorTodd_Trimble
- CommentTimeSep 7th 2015
Harry actually asked a good question back in #2, and the article affine variety referred, uncomfortably, to the article affine space which is almost entirely about vector spaces without origin. I therefore tried to add a few words of disambiguation in the Idea section of affine space. (Probably not optimally, but it’s late and I’m a little tired!)
-
- CommentRowNumber6.
- CommentAuthorzskoda
- CommentTimeSep 8th 2015
- (edited Sep 8th 2015)
3 “There is a bifurcation of meanings: affine spaces in alg. geom. are a generalisation (and relativisation) of a vector space to other base rings. Affine spaces in the sense at affine space are more of an algebraic abstraction of the structure that appears in Gallilean relativity (for example): a vector space with no origin. In other words, a torsor for the underlying abelian group of a vector space.”
I disagree. The meaning in algebraic geometry is also in the sense of without fixed origin. For the pratical purposes one chooses origin to give the corresponding coordinate ring, but it is assumed that the automorphisms do NOT respect the origin. True, a vector space, or generally a module over a commutative ring can be underlying space of a scheme/variety in the sense that one takes the spec of symmetric algebra of the dual can be raised to a functor which is studied in much detail in expositions like SGA3. There are conditions on the rings and modules to have a reasonable result.
4 I also disagree. The vector space can be equipped with a sheaf of rings or not, a module can be equipped or not. When it is equipped it will give rise to a scheme, otherwise not. Specially if you work over a ground scheme, there is an additional structure. Hence Spec of symmetric algebra is not a generalization of a vector space but a result of a functor from modules to schemes.
-
- CommentRowNumber7.
- CommentAuthorMike Shulman
- CommentTimeJan 11th 2016
I added to affine space the definition discovered by Todd here.
What is the semicartesian tensor product induced on by this embedding in ? It seems to take an -dimensional affine space and an -dimensional affine space to an -dimensional one. I’m having trouble picturing it with any other definition of affine space.
-
- CommentRowNumber8.
- CommentAuthorKarol Szumiło
- CommentTimeJan 11th 2016
Shouldn’t this be the affine space that classifies the “bi-affine maps”, i.e. maps affine in each variable separately? (Similarly to the universal property of the tensor product of vector spaces.) That’s not very explicit, but neither is any coordinate free description of the tensor product.
At the first glance the numbers seem to be off, but I think they actually work out. For example the tensor of two -dimensional affine spaces has dimension and the general form of a bi-affine map is with which has affinely independent parameters. (My choice of coordinates is not pretty, I’m taking as an affine basis of .)
-
- CommentRowNumber9.
- CommentAuthorTodd_Trimble
- CommentTimeJan 11th 2016
- (edited Jan 11th 2016)
Thanks for taking the initiative, Mike!
The theory of affine spaces is a commutative theory, and so the monoidal category of affine spaces is closed and Karol’s interpretation of the tensor product in terms of bi-affine maps is the appropriate one. Consequently the tensor distributes over coproducts. Now we can set up a numerical consistency check: given that the coproduct of an -dimensional and an -dimensional is , as one would expect from taking formal Minkowski sums, we can tensor with a -dimensional and check that the numbers work out. Then one can go further and do an induction argument: an -dimensional affine space is an -fold coproduct of copies of the -dimensional affine space , and so we get
since the terminal is the monoidal unit. Since an economical description of the dimension of coproducts of affine spaces is that we are “conjugating” ordinary addition by “plus ”, the coproduct of copies of the -dimensional would be .
-
- CommentRowNumber10.
- CommentAuthorDmitri Pavlov
- CommentTimeJan 11th 2016
Is it possible to give a definition of a projective space analogous to the given definition of an affine space?
I would at least expect an unbiased Lawvere-style definition to make sense. Of course, there is always the question of what maps do we take as morphisms of projective spaces; if we require maps that are everywhere defined, then projective spaces don’t have finite products, and adjoining these gives us a rather complicated structure. (Or does it?) On the other hand one could try to allow partial maps as morphisms, but I’m not sure how to make these into a category.
-
- CommentRowNumber11.
- CommentAuthorKarol Szumiło
- CommentTimeJan 11th 2016
- (edited Jan 11th 2016)
On second thought I don’t think I should’ve included “” in my parametrization of bi-affine maps. But on the other hand the dimension of the affine space of affine maps is also not something completely obvious. E.g. the dimension of the space of affine maps from a -dimensional space to itself is . So perhaps this does work out after all.
-
- CommentRowNumber12.
- CommentAuthorTodd_Trimble
- CommentTimeJan 11th 2016
The dimension of the space of affine maps from an -dimensional affine space to an -dimensional one should be , if you think of such an affine map as being of the form where is a matrix (with respect to coordinatizations, including choice of origins) and is a vector of the codomain.
This can be made more categorically respectable looking by writing an -dimensional as a coproduct of copies of the terminal which is the monoidal unit/internal Hom unit, so that
where the dimension of cartesian products of affine spaces is calculated just as for vector spaces (by adding). So the dimension is .
-
- CommentRowNumber13.
- CommentAuthorMike Shulman
- CommentTimeJan 12th 2016
Thanks, Todd and Karol! Would one of you care to record this at affine space?
Dmitri, that’s an interesting question. One way to do it would be to observe that once you fix a line in a projective space to be “at infinity”, then the points not on that line are an affine space. Since two points determine a line, any -ary operation of an affine space yields an -ary operation of a projective space… but one whose domain is defined by disequalities, so it’s not algebraic. What did you have in mind?
-
- CommentRowNumber14.
- CommentAuthorTodd_Trimble
- CommentTimeJan 12th 2016
I have added some of the material above under a section “Closed monoidal structure” in affine space.
-
- CommentRowNumber15.
- CommentAuthorMike Shulman
- CommentTimeJan 12th 2016
Thanks! I added a remark that allows the empty set (since the definitions at the top of the page currently don’t). I don’t personally really know whether I think the empty affine space should be allowed, but the page should be internally consistent.
-
- CommentRowNumber16.
- CommentAuthorTodd_Trimble
- CommentTimeJan 12th 2016
Oh, of course. Thanks!
1 to 16 of 16