nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
nLab > Latest Changes: circle of entries surrounding infinitesimal neighour
Bottom of Page1 to 13 of 13
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeOct 7th 2009
started infinitesimal neighbour and began creating a circle of entries surrounding this:
infinitesimal path infinity-groupoid in a smooth topos; path infinity-groupoid in a smooth topos; simplex in a lined topos
This is heading in the direction of giving a full discussion of
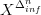 for X a microlinear space, mentioned presently already at differential forms in synthetic differential geometry. I though i could just point to the literature for that, but not quite, apparently. Anders Kock discusses this for X a "formal manifold", an object with a cover by Kock-Lawvere vector spaces. But it should work a bit more generally using microlinear spaces, as indicated in the appendix of Models for Smooth Infinitesimal Analysis. There is an obvious general-nonsense definition wich I discuss, but I need yet to insert discussion of that and how this reproduces Kock's definition (but I think it does).
for X a microlinear space, mentioned presently already at differential forms in synthetic differential geometry. I though i could just point to the literature for that, but not quite, apparently. Anders Kock discusses this for X a "formal manifold", an object with a cover by Kock-Lawvere vector spaces. But it should work a bit more generally using microlinear spaces, as indicated in the appendix of Models for Smooth Infinitesimal Analysis. There is an obvious general-nonsense definition wich I discuss, but I need yet to insert discussion of that and how this reproduces Kock's definition (but I think it does).It has been an esteemed insight for me that the best way to think of all these constructions of "combinatorial differential forms" (still have to expand the discussion of those at differential forms in synthetic differential geometry) is by organizing them into their natural simplicial structures and then noticing that the model category structure available in the background allows us to think of the resulting simplicial objects in the topos as interna oo-groupoids. I think this must clearly the nLab way of thinking about this, so I created entries with the respective titles.
You may have noticed that on my personal web I am developing the further step that goes from (infinitesimal) path oo-groupoids of objects in a 1-topos to (infinitesimal) path oo-groupoids of objects in a "smooth (oo,1)-topos". I don't want to impose that fully (oo,1)-material on the main nLab as yet, before this is further developed, but the bits now added that just have oo-groupoids of paths in a 1-topos object is straightforward enough to warrent discussion here. i think.
While working on this, I also did various minor edits on the synthetic differential geometry context cluster, such as
splitting off lined topos from smooth topos
rewriting the introduction at Models for Smooth Infinitesimal Analysis (the previous remarks are by now better explained in the corresponding sub-entries and the new summary is supposed to get the main message of the book across better). Also created section headers there for each of the single models, which I hope I'll eventually describe there in a bit more detail each. Those toposes
 and
and  they have there are mighty cool, I think, giving not only a well-adapted model for SDG but on top of that an implementation of nonstandard analysis, and of distribution theory. I am thinking that the toposophers among my co-laborants might enjoy looking at their smooth natural number object in
they have there are mighty cool, I think, giving not only a well-adapted model for SDG but on top of that an implementation of nonstandard analysis, and of distribution theory. I am thinking that the toposophers among my co-laborants might enjoy looking at their smooth natural number object in  a bit more. It's fun and seems to be much more relevant than seems to be widely appreciated.
a bit more. It's fun and seems to be much more relevant than seems to be widely appreciated.Notice that at simplex in a lined topos I am asking for a reference. It's this standard construction of simplices as collpsed cylinders on lower dim simplicies. I don't think I should re-invent that wheel. What's the canonical reference for this general construction?
Finally please notice that all entries mentioned above are more or less stubby for the moment and need more work. But I thought it was about time to drop a latest-changes alert here now, before waiting longer.
-
- CommentRowNumber2.
- CommentAuthorEric
- CommentTimeOct 7th 2009
- (edited Oct 7th 2009)
Hi Urs,
When we first started working on discrete geometry, I had just spent years unsuccessfully getting it to work on my own. The reason I failed is that I was working with simplices. It turns out that we HAD to work with cubes to get things to work. So whenever I see you getting hung up with simplices, I always wonder why you expect things to work out nicely with simplices when we already showed that simplices won't work.
Is what concerns you a totally unrelated concept?
The lesson I learned is that simplices are great for doing topology, but fall short when you want to do geometry (or anything involving a metric, gauge, size, length, volume, etc). I'm probably confused.
Edit: I should add that differences between simplices and cubes might blur away in the "continuum limit", i.e. there may not be significant differences between infinitesimal simplices and infinitesimal cubes. I was talking about "finite" simplices and "finite" cubes.
Edit^2: I know the title says "infinitesimal", but I think "infinitesimal" can and should be thought of as a limit of "finitary", so I think getting things to work in a finitary framework and then taking "infinitesimal limits" should reveal underlying structure. But you know I am biased...
Edit^3: Interesting. Looking at Models for Smooth Infinitesimal Analysis, I see you talking about full and faithful forgetful functors
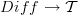 . Here,
. Here, 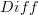 is the category of smooth manifolds. I wonder how messy things get when you instead want to work with "smooth manifolds with metrics", e.g. Riemannian or Lorentzian manifolds. Those would seem to be more important for physical applications. If you are only concerned with smooth manifolds without metrics then differences between cubes and simplices are probably moot.
is the category of smooth manifolds. I wonder how messy things get when you instead want to work with "smooth manifolds with metrics", e.g. Riemannian or Lorentzian manifolds. Those would seem to be more important for physical applications. If you are only concerned with smooth manifolds without metrics then differences between cubes and simplices are probably moot. -
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeOct 8th 2009
Eric,
there are two different roles that the shapes (simplicies, cubes, etc) play, and it is important to distinguish these, eventhough they are closely related:
on the one hand we may consider geometric objects of certain shape. This is what you have in mind. And indeed, for many purposes of concrete geometry cubes are much more convenient than simplices. It is no coincidence that most of the texts n synthetic differential goemetry, for instance, give the cubical definition of differential forms. This is what you have in mind, and you are right about it.
But then there is another aspect: abstract shapes are used as cells in higher categories. Here the thing is that one needs a good "homotopy theory" on the collection of such shapes, to say all the things that one want to say in higher category theory. Such as: this is a wekk oo-functor that induces an equivalence of oo.categories.
In principle one certainly expects that good homotopy theories exist for all kinds of shapes. See the recent paper by Borisov discussed on the blog!
But it is a fact of life that currently, planet Earth, beginning of the 21st century, the only really well-develiped homotopy theory is that based on simplicial sets.
Therefore it may happen that structures that naturally arise as cubical sets are revamped into simplicial sets just so that one can better handle them as oo-categorical structures.
In a better world we wouldn't have to do this. But right now this is the state of the art.
Incidentally, while you wrote your message above I figured out that "reinvention of the wheel" mentioned above in that I thought of a concrete algorithm to map the cubical object of k-cubes in a space into a simplicial object -- without actually changing the geometry of the objects! -- just changing perspective on how we think of them all as glued together to an oo-categorical structure.
I have typed this now into the old entry
I have also restrcutured and edited that entry, (but it deserves more attention, still). See the section on fundamental geometric oo-categories-
This discussion ends with an exercise. I have drawn that on paper, but can't typeset it right nosw, But maybe if you have a minute you may want to draw the evident picture of how the construction I give there picks n-simplices inside cubes.
I should say that it is late at nighr here, so be careful with the text. But I checked the proof of the assertion given there carefully. It should be right.
In fact, now that I did re-invent that wheel, I'd be grateful if other laborants could have a look and see if they remember a standard reference where this is given.
-
- CommentRowNumber4.
- CommentAuthorMike Shulman
- CommentTimeOct 8th 2009
But it is a fact of life that currently, planet Earth, beginning of the 21st century, the only really well-develiped homotopy theory is that based on simplicial sets.
While I know what you mean, the obvious objection from the peanut gallery is "hey, what about topological spaces?"
-
- CommentRowNumber5.
- CommentAuthorEric
- CommentTimeOct 8th 2009
- (edited Oct 8th 2009)
<p>Hi Urs,</p> <p>Thanks.</p> <blockquote> there are two different roles that the shapes (simplicies, cubes, etc) play<br> [snip]<br> on the one hand we may consider geometric objects of certain shape.<br> [snip]<br> But then there is another aspect: abstract shapes are used as cells in higher categories. </blockquote> <p>Hmm... in my mind, I guess I think of these two as the same thing. My motivation for trying to follow all this stuff in the first is that I think spacetime IS a higher category. That's why I'm excitedly awaiting Grandis' new book and to learn more about the directed homotopy hypothesis.</p> <p>Edit: By the way, I just saw your comment on <a href="https://ncatlab.org/nlab/show/interval+object">interval object</a></p> <blockquote> However, while cubes are nice for many purposes, it is a sad fact of life that the <a href="https://ncatlab.org/nlab/show/homotopy+theory">homotopy theory</a> for cubical structures (while certainly it does exist in full beauty in principle) is much less well developed to date (maybe that will change in the future) than that of simplicial structures. For many purposes in <a href="https://ncatlab.org/nlab/show/higher+category+theory">higher category theory</a>, therefore, it will be useful to take a slightly different perspective on <img src="/extensions/vLaTeX/cache/latex_2b2e3638e9d47f1df3225fc25134925f.png" title="X^\Box" style="vertical-align:-20%;" class="tex" alt="X^\Box" />, without essentially changing it. </blockquote> <p>I actually don't expect cubes to offer too much for homotopy theory over simplices. Where I expect them to help things tremendously is with <a href="https://ncatlab.org/nlab/show/directed+homotopy+theory">directed homotopy theory</a>. Roughly, I think about it like:</p> <p>Space <img src="/extensions/vLaTeX/cache/latex_f560021d5b5c4369bfb378b354108869.png" title="\leftrightarrow" style="vertical-align:-20%;" class="tex" alt="\leftrightarrow" /> Homotopy Theory</p> <p>Spacetime <img src="/extensions/vLaTeX/cache/latex_f560021d5b5c4369bfb378b354108869.png" title="\leftrightarrow" style="vertical-align:-20%;" class="tex" alt="\leftrightarrow" /> Directed Homotopy Theory</p> <p>Cubes are good not only for (Lorentzian) metric spaces, but also for the closely related, but probably more general <a href="https://ncatlab.org/nlab/show/directed+space">directed space</a>s.</p> <p>I suspect that the move to directed homotopy theory will be as liberating to higher category theory as the move to Minkowski space was for physics.</p> -
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeOct 8th 2009
<div> <blockquote> "hey, what about topological spaces?" </blockquote> <p>Right. I mean <em>combinatorial</em> models for homotopy theory.</p> <p>I'll switch to oo-stacks modeled as cubical presheaves as soon as I know the analog of the first few lemmas at <a href="http://ncatlab.org/schreiber/show/path+%E2%88%9E-groupoid">schreiber:path oo-groupoid</a> in the cubical model.</p> <blockquote> My motivation for trying to follow all this stuff in the first is that I think spacetime IS a higher category. </blockquote> <p>Yes. We want the <a href="http://ncatlab.org/schreiber/show/path+%E2%88%9E-groupoid">path oo-groupoid</a> <img src="/extensions/vLaTeX/cache/latex_a88a29e3be9f18ea5b32041789fcca1a.png" title=" \Pi(X) " style="vertical-align: -20%;" class="tex" alt=" \Pi(X) "/> of spacetime X.</p> <p>What I am trying to tell you is that because and just because cubical models for general oo-categories are underdeveloped, do we force what may naturally arise as a cubical structure here into a simplicial structure -- just so that we can compute homotopy limits/colimits etc. It's purely a matter of computational practicability. In 50 years, when the cubical homotopy theory is fully available, we will no longer have to do this and may look back with regret at all the pain we went through forcing obvious cubical models into simplicial ones.</p> <p>But whatever it is, the important point is that this is not of fundamental intrinsic importance, but only about the tools we apply to reason about reality. We know essentially that a better tool than available currently must exist, but the fact of life is that right this moment we don't have it.</p> <p>So instead of complaining, you should now rejoice ;-) that I gave at <a href="https://ncatlab.org/nlab/show/interval+object">interval object</a> that explicit construciton which satisfies all your cubical desires while at the same time being tractable by simplicial methods.</p> <p>There is, I think, by the way, a very deep abstract nonsense reason that supports your preference for cubes. You can see this in the axiomatics of synthetic differential geometry, in David Spivak's thesis (first version) and in the new material that John Baez and Jim Dolan recently discussed on the blog:</p> <p>namely of fundamental importance seems to be the notion of a <a href="https://ncatlab.org/nlab/show/lined+topos">lined topos</a>. A category whose objects behave like some kind of spaces and where one particular object R is singled out, the one that plays the role of the standard line <img src="/extensions/vLaTeX/cache/latex_8decf146056a3e7883740f6014a12521.png" title=" \mathbb{R} " style="vertical-align: -20%;" class="tex" alt=" \mathbb{R} "/>.</p> <p>The point is that givem just this input data and abstract nonsense, there is naturally the co-cubical object consisting of all the cubes R^n built from that line.</p> <p>This is really what's going on at the heart of synthetic differential forms. I am about to write more about this at <a href="https://ncatlab.org/nlab/show/infinitesimal+neighbour">infinitesimal neighbour</a>...</p> </div> -
- CommentRowNumber7.
- CommentAuthorEric
- CommentTimeOct 8th 2009
<div> <p>Very tantalizing! Thanks</p> <p>I guess what I'm hearing is that my intuition might be close to being meaningful, yet the tools are not necessarily there yet.</p> <p>If I had the ability, I would take this as a challenge. I think the payoff for developing cubical tools in (directed) homotopy theory would more than compensate the upfront costs.</p> <p>By the way, you said:</p> <blockquote> Yes. We want the <a href="https://ncatlab.org/nlab/show/path+infinity-groupoid">path infinity-groupoid</a> <img src="/extensions/vLaTeX/cache/latex_2cb0c26752b0317072c8f80dd42659a5.png" title="\Pi(X)" style="vertical-align: -20%;" class="tex" alt="\Pi(X)"/> of spacetime <img src="/extensions/vLaTeX/cache/latex_04d0eb37f084cb02c47fa2a271035fef.png" title="X" style="vertical-align: -20%;" class="tex" alt="X"/>. </blockquote> <p>I would think we want the <a href="https://ncatlab.org/nlab/show/fundamental+category">fundamental category</a> of spacetime. Again, the way I think of it</p> <p>Fundamental Groupoids <img src="/extensions/vLaTeX/cache/latex_f560021d5b5c4369bfb378b354108869.png" title="\leftrightarrow" style="vertical-align: -20%;" class="tex" alt="\leftrightarrow"/> Spaces</p> <p>Fundamental Categories <img src="/extensions/vLaTeX/cache/latex_f560021d5b5c4369bfb378b354108869.png" title="\leftrightarrow" style="vertical-align: -20%;" class="tex" alt="\leftrightarrow"/> Spacetimes</p> <p>This is what I meant by my interest in the directed homotopy hypothesis. But, of course, I have only a vague picture of all the moving pieces.</p> </div> -
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeOct 8th 2009
Okay, right, I know what you are thinking of re directed spaces, spacetime, category. Yes, I agree, this is another important point to be addressed.
I have to say, by the way, that it is not at all clear to me why cubes are automatically better suited to describe directed spaces than simplices.
On the contrary, when I queried the cat theory mailing list a few weeks ago on the status of the "directed homotopy hypothesis" the result was essentially a bunch of replies saying that various cubical definitons exist, and one single reply by somebody who claimed that he was about to put out an article actually proving the directed homotopy hypothesis for (oo,1)-categories vs 1-directed spaces. And that apparently used simplicial methods.
But in any case, here, too, I expect that when the theory is available, it will be available both in a simplicial and a cubical version. All these shapes are just means to access a deeper reality that doesn't care about us stupid things wanting to describe evereything using just a single standard shape in a homotopica world where all shapes may tranmute anyway
-
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeOct 8th 2009
Eric, one more comment, to reemphasize what I said before:
this "arbitrariness of shapes" I am talking about concerns the shapes of cells in higher categories.
I see this as related to but different from the "geometric" shapes.
In particular, given that we are talking about line objects: these naturally form cubes, whether these are later arranged simplicially or cubically or hexagonally.
Notice that the dg-algebra of n-dimensional diamonds is the tensor product of a line object with itself: of the object that is the dg-algebra of 1-dimensional diamonds.
This is getting us into the not-so-well studied realm of noncommutative derived algebraic geometry, but it is kind of clear that there should be an oo-topos of oo-sheaves on duals of dg-algebras and that this 1-d diamonds algebra makes that into a smooth lined oo-topos. In such a context dg-algebras of diamonds would be natural and deeply rooted in abstract nonsense.
So, you see, I am trying to say that your intuition is perfectly right if you stay clear of identifying geoemtric with categorical shapes in too naive a fashion. Instead, your intuition is telling you to come along the direction I am trying to describing here: smooth oo-toposes with line objects.
I am not done yet, but this is the take-home message of schreiber:structural context for fundamental quantum physics:
a smooth oo-topos is the context for smooth cohomology and hence kinematics.
a smooth oo-topos equipped with a line object is the context for differential cohomology and dynamic.
That's the idea, at least.
-
- CommentRowNumber10.
- CommentAuthorEric
- CommentTimeOct 8th 2009
- (edited Oct 8th 2009)
<blockquote> somebody who claimed that he was about to put out an article actually proving the directed homotopy hypothesis for (oo,1)-categories vs 1-directed spaces. And that apparently used simplicial methods. </blockquote> <p>Is there a difference between cubes and simplices when talking about (oo,1)-categories vs 1-directed spaces? It seems like anything about dimension one is blurred away. (as if I knew what (oo,1)-categories and 1-directed spaces were! :))</p> <p>I think one point from your exercise on <a href="https://ncatlab.org/nlab/show/interval+object">interval object</a> is related to the fact that a directed cube can be decomposed into directed simplices (obviously).</p> <p>For example, to traverse a directed 3-cube, there are 6 distinct directed 1-paths</p> <p><img src="/extensions/vLaTeX/cache/latex_86ac5a5f0e38d75f56caf2fcc5523c4e.png" title="(0,0,0)\to(0,0,1)\to(0,1,1)\to(1,1,1)" style="vertical-align:-20%;" class="tex" alt="(0,0,0)\to(0,0,1)\to(0,1,1)\to(1,1,1)" /><br></p> <p><img src="/extensions/vLaTeX/cache/latex_88eefa75d76ee673603f47e705cb1391.png" title="(0,0,0)\to(0,0,1)\to(1,0,1)\to(1,1,1)" style="vertical-align:-20%;" class="tex" alt="(0,0,0)\to(0,0,1)\to(1,0,1)\to(1,1,1)" /><br></p> <p><img src="/extensions/vLaTeX/cache/latex_9ad57efef2163b702a8e10823456662c.png" title="(0,0,0)\to (0,1,0)\to (0,1,1)\to (1,1,1)" style="vertical-align:-20%;" class="tex" alt="(0,0,0)\to (0,1,0)\to (0,1,1)\to (1,1,1)" /><br></p> <p><img src="/extensions/vLaTeX/cache/latex_be9e479fbad8ae38e957207adc99d04c.png" title="(0,0,0)\to (0,1,0)\to (1,1,0)\to (1,1,1)" style="vertical-align:-20%;" class="tex" alt="(0,0,0)\to (0,1,0)\to (1,1,0)\to (1,1,1)" /><br></p> <p><img src="/extensions/vLaTeX/cache/latex_bdb9f43f0743426937b88209b9302aa1.png" title="(0,0,0)\to (1,0,0)\to (1,0,1)\to (1,1,1)" style="vertical-align:-20%;" class="tex" alt="(0,0,0)\to (1,0,0)\to (1,0,1)\to (1,1,1)" /><br></p> <p><img src="/extensions/vLaTeX/cache/latex_bdb9f43f0743426937b88209b9302aa1.png" title="(0,0,0)\to (1,0,0)\to (1,0,1)\to (1,1,1)" style="vertical-align:-20%;" class="tex" alt="(0,0,0)\to (1,0,0)\to (1,0,1)\to (1,1,1)" /><br></p> <p>I think of these directed paths as requiring 3 ticks of a clock (or 3 time steps) to traverse. With a slight reinterpretation, we can think of these 6 directed (3 step) paths as representing 6 directed 3-simplices, i.e. the directed 3-cube is the union of 6 directed 3-simplices.</p> <p>In the end, whether we want to think of it as directed 3-cubes or directed 3-simplices doesn't matter much. The important thing (and maybe I am misguided on this) is that the simplices <i>come from decomposing cubes</i>. I think it would be difficult (if not impossible) to fill an arbitrary directed spaced with directed simplices in a consistent manner that does not come from the decomposition of directed cubes. The problem is that the nodes of the directed simplices will not always corresponds to directed 1-paths in the original space, i.e. the path traversing the simplex might wrap back on itself in a non-causal manner.</p> <p>Ok! Now that I wrote that down, I see my logic is possibly flawed because I think maybe you <i>can</i> order the nodes of the simplices so all paths are consistent with the order of the original directed space. Hmm...</p> <p>One problem I can think of that may not be of significance, but my gut tells me it is...</p> <p>If you take an arbitrary directed 3-space and decompose it into 3-simplices, you CAN order the nodes in such a way that is consistent with the causal direction. However, you will have trouble "gluing" them together depending on the meaning of "glue".</p> <p>In a directed space there are "special" directed 1-paths that can probably be called "light-like paths" or "maximum velocity paths". With cubes, all edges can be light like (or maximum velocity). With simplices, some edges MUST be time like in order to glue them together.</p> <p>Ok! That is the argument that makes sense to me. I'll say it one more time, just to get it straight in my head.</p> <p>I think cubes are better than simplices for studying directed homotopy theory because a decomposition of a directed space into cubes can consist entirely of light-like 1-paths. With a simplicial decomposition, some of the edges must necessarily be time-like or worse, space-like. You can probably even show that if any edge of a simplicial decomposition is time-like, there must be a space-like edge as well.</p> <p>Maybe the classification of paths in a directed space into time-like, space-like, and light-like are not important for directed homotopy theory, but I suspect that it just might make life easier (maybe).</p> <p>Edit: Of course, this all rides on the validity of the <a href="http://ncatlab.org/ericforgy/show/diamonation">diamond conjecture</a>.</p> -
- CommentRowNumber11.
- CommentAuthorEric
- CommentTimeOct 9th 2009
I added some diagrams to your exercise at interval object. I hope they are helpful!
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeOct 9th 2009
Wow, thanks Eric. Yes, that's what I was thinking of.
Maybe one thing: the construction I describe picks one specific sub-simplex inside a cube (after we have fixed our coordinate axes.) It would be nice if we could show precisely which one and how it is labeled.
With the graphics you already have created it would be nice ( am not requesting you to do that, but if you have a spare second I would enjoy it if you did!) to choose labels for the three coordinate axes of R^3 and then identify and label the simplex obtained from that using the description I gave.
What I mean is this: if we choose
x1 to run to the right
x2 to run upwards
x3 to run away from the viewer
then the 3-simplex according to the definition is the following
the 0-vertex is the left-bottom-front one
the 1-vertex is the right-bottom-front one
the 2-vertex is the right-top-front one
the 3-vertex is the right-top-rear one
Would it be possible that you take one of your tetrahedra, enlarge it a bit and label it like this? That would give a nice illustration of the abstract procedure.
-
- CommentRowNumber13.
- CommentAuthorEric
- CommentTimeOct 9th 2009
- (edited Oct 9th 2009)
I was afraid you were going to ask for that :)
I'll put it on my to do list (which is pretty long right now as I'm moving to Hong Kong!) :)
Edit: Did my rambling about light-like, time-like, and space-like edges make any sense?
It seems to me that a directed space comes with a concept of maximum velocity. The nice thing about cubes as opposed to simplices for directed spaces with a maximum velocity is that the directed edges of cubes can all be "maximum velocity edges".
1 to 13 of 13