nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeAug 15th 2010
- (edited Aug 15th 2010)
For a manifold and a (good) cover with Cech nerve and its geometric realization , is the canonical map a Hurewicz fibration?
-
- CommentRowNumber2.
- CommentAuthorDavidRoberts
- CommentTimeAug 16th 2010
Actually, one could try to say some interesting things here. First, if good covers are numerable, then is shrinkable for a good cover. This depends on what sort of manifold you are looking at. Paracompactness of the manifold should give us that good covers are close to numerable, if not actually numerable (probably only need point-finiteness of the good cover of a paracompact manifold to ensure that the cover can be itself numerable). Note that a shrinkable map is a Dold fibration – but not all Dold fibrations are Hurewicz fibrations.
Why do you need this?
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeAug 16th 2010
- (edited Aug 16th 2010)
Thanks, David, that’s very useful!
Do you happen to know also something about the following refinement of the question:
suppose the manifold with numerable open cover is smooth. Then its Cech nerve realization is a space that is cell-wise smooth or something like that.
Let be smoothly contractible by a smooth homotopy . Let
be the pullback of the nerve of the Cech cover to the correspondence space. I want to find a lift in the diagram
which is cell-wise smooth.
-
- CommentRowNumber4.
- CommentAuthorDavidRoberts
- CommentTimeAug 16th 2010
- (edited Aug 17th 2010)
OK. Given the numerable cover , there is a cover refining (which is neither open nor closed (Edit: the refining cover, that is)) of the form where is a partition, namely a closed cover of I which is the disjoint union of a finite number of sub-intervals of that only intersect at their endpoints, and is a cover (this is due to Dold). If is a finite cover (say if is compact) we can obviously refine this to for some partition .
So we get a commuting diagram
I don’t know if it true, but I wonder if a result like holds. I suspect that this map (call it ) is shrinkable. A simple example should give some insight, but I can’t think of one right now. Since is shrinkable, then it has a section. Now the trick is getting the putative section of to have the right initial values (i.e. over , or rather the lift of this to ) so that we get a lift in the original square.
Unfortunately I cannot say anything intelligent about smoothness at present.
For reference to the result of Dold, see A.2.19 in Dold’s Lectures on Algebraic Topology (search for ’stacked covering’ in Google books, for example)
Hope this helps some more.
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeAug 16th 2010
Thanks again, David. Indeed, that does help some more. I’ll look at the reference by Dold that you mention.
One minor question. You write:
Given the numerable cover , there is a cover refining (which is neither open nor closed)
Why do you say it’s not open? It is the pullback of an open cover along a continuous map.
-
- CommentRowNumber6.
- CommentAuthorDavidRoberts
- CommentTimeAug 16th 2010
is an open cover, but the cover is not (I can see why you ask - my sentence is not clear). It is a refinement in the sense that there is a commuting triangle
I may not have got the indexing set right for the refinement, see the reference by Dold I gave to clear that up.
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeAug 16th 2010
- (edited Aug 16th 2010)
Ah, I see.
Still have to look at Dold, will do that now.
By the way, my application for the smoothness is this: I want to prove that every smooth -principal -bundle is locally equivalent to the trivial one, if is obtained by Lie integration of an -Lie algebra.
I already have a proof that every -principal -bundle admits a genuine -connection. That means that for
the cocycle for the -bundle, in total I can construct locally smooth differential forms on with values in the -Lie algebra whose curvature vanishes on all “internal” directions (simplicial directions not along one of the ).
So that’s a morphism . On simplices these forms encode the cocycle, on patches the connection.
Now if I had a pasting diagram
then the total top outer morphism would constitute the homotopy from the given cocycle to the trivial cocycle.
This is (or would be, if it all works as I am expecting it should) the -analog of how you can find a local trivialization of a bundle by choosing a connection on it and then using locally the paralle transport of the connection to identify fibers. In my articles with Konrad we give explicit by-hand formulas for the lifts that do give the above diagram in low categorical degree. Now I would like to find the fully general formulation.
-
- CommentRowNumber8.
- CommentAuthorDavidRoberts
- CommentTimeAug 17th 2010
I think this can be done. Passing to the cover , and choosing a lift of to (I mean restricted to this cover), means for each path , taking a partition of and lifting each subinterval to elements of the cover, to give a path in the groupoid . On taking the geometric realisation (possibly we should be thinking fat realisation? We should check this, or perhaps you know it is ok already) then we should get a span , where the left leg has a map which isn’t a necessarily section, but satisfies for . Also we would have rel endpoints (actually a reparameterisation).
Now I think that it is not unreasonable to repeat this sort of argument for finding a map which is to above as is to , namely that it is a section restricted to .
This is all heuristic, but it seems to me to be a hopeful proposition.
-
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeAug 17th 2010
I think this can be done.
This would be nice! Have to run to the train now. But let's sort this out!!
(I had trouble with reading Dold, by the way. Google books wouldn't show me many pages, and all in all I didn't get a coherent impression of what he is writing about. Might have to try to track down a paper copy. But maybe the important theorem is the one you already mentioned. Somebody should put this into the nLab.)
-
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeAug 17th 2010
- (edited Aug 17th 2010)
It is good that we are talking about this. As so often, just verbalizing a problem sometimes makes it evaporate.
I had originally thought I should pass to the geometric realization to construct the lift using properties of fibrations of topological spaces. But in your last meessage you (David) actually amplify that we should just construct the lift at the level of groupoids and only then pass to the geometric realization. Because it really suggests that we find a lift
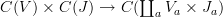 I think that's in fact an easy route to solve the problem, as you indicate. The lift at the level of groupoids is just the problem as it already appears in categorical degree 1. I think this is under control.
I think that's in fact an easy route to solve the problem, as you indicate. The lift at the level of groupoids is just the problem as it already appears in categorical degree 1. I think this is under control.I'll think a bit and write a bit and then will get back to you.
-
- CommentRowNumber11.
- CommentAuthorAndrew Stacey
- CommentTimeAug 17th 2010
(Urs, you’ve flipped your formatter from MarkdownItex to Markdown again)
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeAug 17th 2010
- (edited Aug 17th 2010)
(thanks, Andrew)
David, I’ll have to ask you the following since I still couldn’t really look at the Dold reference (maybe later today I get a chance).
Since is a cover with a partition of , it would seem to follow that in fact for fixed the map is surjective, right? Because for fixed in the interior of one we have by definition of partition that there is no other such that would also be in . Hence it must be true that for every , there is a lift of to , hence a lift of to .
Am I understanding you correctly here?
If this is so, then we could do the following:
form the joint intersection space . This is still a cover (if my above understanding is correct). A lift of to amounts to choosing for each interval a compatible lift to .
Then I think we should get a functor that covers by the rule
where is our lift of the contraction.
In words this would mean that: we run with along until the flow on the s makes any one of them come close to the boundary of a patch. Then we allow every to switch patches, then we continue to run the flow a bit more, until we need to pause and allow everyone to jump patches again.
In one way or other we need to find a formalization of this story.
-
- CommentRowNumber13.
- CommentAuthorzskoda
- CommentTimeAug 17th 2010
- (edited Aug 17th 2010)
Did you compare the Hurewicz fibration condition to the characterization via Hurewitz connection which is pretty close to your approach to everything via cocylinders and Brown’s factorization lemma which are in a very siilar setup ? It may help by chance ? P.S. I have sent you a better link to Dold at gmail.
-
- CommentRowNumber14.
- CommentAuthorUrs
- CommentTimeAug 17th 2010
I guess it should be true that if you start with a smooth principal -bundle with -connection, then its geometric realization is a Hurewicz fibrtation and the -connection provides the Hurewicz connection. But I haven’t formalized this yet.
By the way, is there a small typo in Hurewicz connection: in the statement of the theorem, it has
iff there exists at least one Hurewicz connection for
Shouldn’t this be
iff there exists at least one Hurewicz connection for
?
-
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeAug 17th 2010
started stacked cover
-
- CommentRowNumber16.
- CommentAuthorzskoda
- CommentTimeAug 17th 2010
You are right, though it is partly the matter of language. The Hurewitz connection is a section of $\pi_!$, so in a way it is associated to $\pi$ and also to $\pi_!$. You can safely remove the $!$ in the statement.
On the other hand, as you read in the bottom section of the article Hurewicz connection, the usual connections do not provide Hurewicz connections but a smooth analog (not smooth case). That is, one has to replace the cocylinder etc. with their smooth analogues.
-
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeAug 17th 2010
David,
I am now looking at Dold in detail. Wouldn’t your restatement of the result he describes require that we have a finite bound on his function ?
-
- CommentRowNumber18.
- CommentAuthorDavidRoberts
- CommentTimeAug 18th 2010
Since is a cover with a partition of , it would seem to follow that in fact for fixed the map is surjective, right?
I don’t think so - the s are open nhds of that, dragged along (i.e. considering the homotopy ), pass through a finite list of s (actually can pass through infinitely many, but we can select a finite subset which does pass through) such that for each connected component , is contained completely within the th open set in .
In particular, we can’t do this:
because we cannot find a single which supposedly is the refinement of all the , unless the is a finite cover. I also don’t know what you mean by
…the joint intersection space
as this is pretty much always empty (if we take the intersection as subspaces) or otherwise non-interesting (if we take the pullback).
Actually I think I see where the confusion arises:
…with a partition of …
because each is a partition of , for and all depending on the index , rather that the collection of forming a partition. If you like this can be changed to a partition as in Dold’s statement of the result about stacked covers, namely where the subintervals are of uniform, rational length, depending on .
To get a handle on this, I think the map
and its geometric realisation needs a close inspection. I was hoping that a lift would be obtained by looking at a parameterised reparameterisation, , but this approach is perhaps too naive.
Keep asking questions if this is not clear…
-
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeAug 18th 2010
Yes, that’s what I realized when I read Dold, as indicated by my last question. I read you notation wrong, thought you said that each is an interval such that the collection is a partition of .
So then I am not sure now how that result by Dold will help. But I’ll keep thinking about it.
-
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeAug 18th 2010
- (edited Aug 18th 2010)
To get a handle on this, I think the map […]
I think we can get a topological lift by my original approach, but I am not sure how to make it cellwise smooth:
we have that is a Dold fibration (is this true also for the fat geometric realization?) and can assume without restriction that the contraction is a delayed homotopy (in the sense used at Dold fibration). Then it follows by standard right-lifting-property-yoga that the pullback is itself a Dold fibration, so we can lift in the diagram
where in the bottom horizontal morphism is some smoothing function making this a “delayed homotopy”, too.
1 to 20 of 20