nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
Atrium > Mathematics, Physics & Philosophy: Accepting the Categorical Imperative: defining Categories without ZFC+U+++
Bottom of Page1 to 25 of 25
-
- CommentRowNumber1.
- CommentAuthorStephenGaito
- CommentTimeOct 14th 2009
Call me a "bear of *very* little brain"....
BUT....
I have spent a couple of days vainly searching through the nLab pages (and associated references) looking for a clean, clear, non-circular definition of Category Theory which does NOT use even the ghost of ZF+C+U (+predicateLogic+firstOrderLogic+ + +)....
Alas, I can not find any... what am I missing?
(I see lots of references to the fact that it should exist but no simple non-circular statement).
Does anyone know where to find one?
Preferably listed on one A4 (~8.5x11) page --- since we all know that Category Theory IS simpler to understand than ZFC+U+++ ;-)
Cheers!
Stephen Gaito -
- CommentRowNumber2.
- CommentAuthorJonAwbrey
- CommentTimeOct 14th 2009
Not sure if it's the question you're asking, but it sounds similar to a question that often arises about circularity vs. recursion.
The fact that a definition or specification of System
 refers to a few concepts and terms that happen to be used in System
refers to a few concepts and terms that happen to be used in System 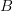 does not necessarily mean that
does not necessarily mean that  depends on the whole of
depends on the whole of 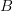 for its def or spec. The question is — How Much of
for its def or spec. The question is — How Much of 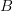 does
does  really need to ground itself, and does the entire system of dependencies eventually ground out?
really need to ground itself, and does the entire system of dependencies eventually ground out?Just my guess, but I think that's the spirit in which MacLane uses language about Metacategories and Metagraphs at the very outset — Out Set ! — of Cat Work Math.
-
- CommentRowNumber3.
- CommentAuthorTodd_Trimble
- CommentTimeOct 14th 2009
- (edited Oct 14th 2009)
I guess the problem is that you see phrases like "set of objects" or "collection of objects" and you're worried that this implicitly refers to some background set theory?
But as a first-order theory, it works the same way as any first-order theory (including ZF, about which no one complains of circularity): the theory as usually presented consists of two sorts
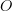 and
and 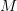 , function symbols
, function symbols 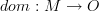 ,
, 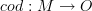 , etc. etc.
, etc. etc.When it comes to modeling category theory, that could be another story, since the sorts are often modeled by sets or classes, but there's plenty of wiggle room: one doesn't need ZF particularly as a background theory.
-
- CommentRowNumber4.
- CommentAuthorJonAwbrey
- CommentTimeOct 14th 2009
- (edited Oct 14th 2009)
The same sort of question arose at the genesis of Generative Transformational Grammar Theory, and here is what Chomsky wrote about it:
In linguistic theory, we face the problem of constructing this system of levels in an abstract manner, in such a way that a simple grammar will result when this complex of abstract structures is given an interpretation in actual linguistic material.
Since higher levels are not literally constructed out of lower ones, in this view, we are quite free to construct levels of a high degree of interdependence, i.e., with heavy conditions of compatibility between them, without the fear of circularity that has been so widely stressed in recent theoretical work in linguistics. (Chomsky, 1975, p. 100).
Chomsky, N. (1975), The Logical Structure of Linguistic Theory, University of Chicago Press, Chicago, IL. Based on a widely circulated manuscript dated 1955.
See my Prospects for Inquiry Driven Systems, § 1.1.3.1. Levels of Analysis for further discussion.
P.S. That link may not work due to quirks in the way MediaWiki handles 2-spaces (= ), but I'll try to fix it later today.
-
- CommentRowNumber5.
- CommentAuthorTobyBartels
- CommentTimeOct 14th 2009
- (edited Oct 14th 2009)
The Lab is very circular, since it doesn't pick a fixed foundation and define everything in terms of that. But one can pick various foundations and try them. Examples:
- Work in first-order classical logic, and pick ZFC. Then a small category may be defined as a set
 , a set
, a set 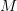 , etc. And a (possibly large) category is not an object in the language, but a statement in the language with several identified free variables.
, etc. And a (possibly large) category is not an object in the language, but a statement in the language with several identified free variables. - Work in first-order classical logic, and pick NBG. Then a category may be defined as a class
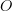 , a class
, a class 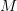 , etc; a small category is a category in which these classes are sets. Despite the different language, this is equivalent to the above.
, etc; a small category is a category in which these classes are sets. Despite the different language, this is equivalent to the above. - Work in first-order classical logic, and pick TG (which is ZFC + universes). Then a category may be defined as a set
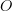 , a set
, a set 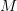 , etc. Relative to any Grothendieck universe
, etc. Relative to any Grothendieck universe 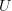 , a
, a 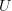 -small category is a category in which these sets are elements of
-small category is a category in which these sets are elements of 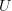 .
. - Work in first-order intuitionistic logic, and pick Aczel's CZF. This works just like ZFC, but you can prove only the ‘constructive’ results.
- Work in first-order classical logic, and pick ETCS. Although ETCS may be summarised as ‘The category of sets is a well-pointed
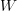 -topos with choice.’, that is on the meta-level; there's nothing about categories in its specificiation in first-order logic. The definitions work the same as in ZFC; although the language is less expressive, you can say all that you need to say to develop category theory.
-topos with choice.’, that is on the meta-level; there's nothing about categories in its specificiation in first-order logic. The definitions work the same as in ZFC; although the language is less expressive, you can say all that you need to say to develop category theory. - Abandon logic and work in Martin-Löf's ITT. Now you must first define a set to be a type with an equivalence relation. Then you can define a strict category to be a set
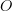 , a set
, a set 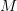 , etc, just as in ETCS. And you can define a (possibly weak) category as a type
, etc, just as in ETCS. And you can define a (possibly weak) category as a type 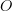 , a type
, a type 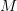 , etc, but with a partial equality relation on
, etc, but with a partial equality relation on 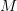 included, so you can talk about equality of parallel morphisms but not equality of objects or equality of morphisms in general. ITT comes with a sequence of universes, relative to which you can consider small categories.
included, so you can talk about equality of parallel morphisms but not equality of objects or equality of morphisms in general. ITT comes with a sequence of universes, relative to which you can consider small categories. - Modify first-order logic into FOLDS and express something like ETCS in that. Actually, the elementary theory of the
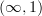 -category of (possibly weak)
-category of (possibly weak)  -groupoids is probably most appropriate here. I don't know the details.
-groupoids is probably most appropriate here. I don't know the details.
You can also combine many of the variations above. For example, you could add NBG-style classes or universes to theories that don't have them, swap out intuitionistic and classical logic, add or remove collection or choice axioms, etc. That doesn't really give any new variations on the definitions, however.
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeOct 15th 2009
I'd think it worthwhile to put such detailed explanation into some nLab page. This reacts to questions that for instance readers of the page foundations or related pages are likely to have again.
I think that whenever anyone explains anything nontrivial here or on the nCafe, it should be made an nLab entry.
-
- CommentRowNumber7.
- CommentAuthorMike Shulman
- CommentTimeOct 15th 2009
What is meant by "a definition of category theory"?
-
- CommentRowNumber8.
- CommentAuthorJonAwbrey
- CommentTimeOct 15th 2009
MS: What is meant by "a definition of category theory"?
That would depend on how one is using the word "theory" — whether pre-theoretically, theory-theoretically, or post-theoretically …
-
- CommentRowNumber9.
- CommentAuthorStephenGaito
- CommentTimeOct 19th 2009
Many many thanks for the helpful comments. Given the comments, the slight delay, in providing my reply, has come from my deciding to go and absorb as much as possible from a couple of texts on First-Order Predicate Logic, as well as to re-read Mike's excellent paper "Set theory for category theory" (ArXiv::math/0810.1279v2) in order to make this reply.
So to begin, I strongly second Urs's request to have Todd and Toby's replies worked into an nLab page which has an explicit link to Mike's paper... all three were directly helpful.
Given these replies and my general reading, I now see that a direct answer to Mike's question would be: The "definition" I am looking for is an axiomatization using First-Order Logic. (Essentially along the lines of Todd's reply).
Alternatively, William Hatcher (in "Foundations of Mathematics"; 1968; W B Saunders Company), gives an explicit morphism based axiomatization of Category Theory as a First-Order Logic with equality/identity, using a predicate of order 3, (K(x,y,z) := "z is the ordered composition of x with y"), and two functions of order 1, (D(x) :=domain and C(x) :=codomain), in 6 axioms. (Objects are intuitively-identified with their identity morphisms). William Hatcher then goes on and provides an explicit extension of these 6 axioms to axiomatize ETCS in 13 additional axioms (all essentially based on the work of Lawvere).
Such an axiomatization provides a clear exhibition of the axioms of Category Theory upon which to base changes.
I will now grant, however, that if I were to work inside an appropriate choice of set-theory, I could get the same effect by giving the more traditional but less axiomatic-formal definition of Category Theory in terms of sets and mappings between these sets. Indeed after re-reading Mike's paper, I think that a good choice, for my purposes, would be to work inside ZFC+U where I make use of two related Universes to define small and large respectively (I think two Universes are sufficient for my needs).
I could, however, translate Mike's question into the higher-level question: Why?
The high-level answer to this question is: I believe that the current definition of Category Theory is (slightly) in-appropriate for a unified definition of (Higher) Category Theory. For example, among other changes, I assert that an appropriate definition of "composition" for the "Higher" aspects of Category Theory is not generally associative.
Given that I believe that there is a better definition of Category Theory, it is incumbent upon me to provide such an "improved" definition.
IF I were to do this, what form should it take, assuming that I accept that everything in a formal definition is itself a Categorical theory (i.e. that I accept the Categorical Imperative)?
I now see that the normal implementation of the Hilbert-Frege formalization program is to use:
- Formal language theory (either as a Categorical or Set-theoretical theory)
- Sentential Calculus (again, either as a Categorical or Set-theoretical theory)
- Predicate Calculus (again.....)
- Model theory (again....)
In each case the required theory can be seen as being either derived as a Categorical or as a Set-theoretical theory, so long as the structures built in these theories are all constructible and hence computable. It is critical that the axioms/theorems/proofs used to axiomatize a theory are checkable in a purely mechanical manner, by, for example, a computer.
However, when we follow the Hilbert-Frege program, we essentially issue a "promissory note" to the effect that the formal structures we are using will all be produced as theories in some axiomatize-able theory that we trust (i.e. that is consistent). Since the Categorical Imperative states that ALL theories are Categorical Theories, I was concerned that, if I changed the basic definition/axiomatization of Category Theory itself, I might invalidate this "promissory note". I now see the answer is probably not (which, given that any "interestingly-useful" axiomatic system can only be proven consistent relative to some other "interestingly-useful" axiomatic system, is good enough).
SO, I must now go away and produce my new and improved definition/axiomatization.... (what fun eh?)
Again, many thanks for the helpful comments!
-
- CommentRowNumber10.
- CommentAuthorJonAwbrey
- CommentTimeOct 19th 2009
Good night, sweet principia …
-
- CommentRowNumber11.
- CommentAuthorStephenGaito
- CommentTimeOct 19th 2009
PS: further to my previous comment....
My real problem is, in particular, that one of the simplest categorical ways to define simplicial sets (which will be the basis of my "new" definition of Category Theory) is via the functor category [\Delta^{op}, Set].
However if I change the underlying definition of Category Theory, does this invalidate the categorical definition of simplicial sets? I do not think so.... but there is some work to be done to show this... and some care would be prudent in showing this....
Alas, I am not sure exactly how Set changes.... I can embed the usual category Set into the new-category Set but some thought will be needed to understand its effect on things like: [\Delta^{op}, Set]....
Hence my original concerns....
Oh what fun mathematics is ;-)
-
- CommentRowNumber12.
- CommentAuthorMike Shulman
- CommentTimeOct 19th 2009
I assert that an appropriate definition of "composition" for the "Higher" aspects of Category Theory is not generally associative.
If by this you mean that in a higher category, composition of morphisms will not necessarily be associative, this is well-understood, and most existing definitions of n-categories allow nonassociative compositions.
(The nlab page on n-category doesn't say anything about how important it is that the notion is weak! How did that happen?)
-
- CommentRowNumber13.
- CommentAuthorTodd_Trimble
- CommentTimeOct 19th 2009
Jon, I think this is one of your less successful puns, since that's supposed to be a hard c in 'principa'.
-
- CommentRowNumber14.
- CommentAuthorTodd_Trimble
- CommentTimeOct 19th 2009
"The high-level answer to this question is: I believe that the current definition of Category Theory is (slightly) in-appropriate for a unified definition of (Higher) Category Theory. For example, among other changes, I assert that an appropriate definition of "composition" for the "Higher" aspects of Category Theory is not generally associative."
Stephen, I must confess that I'm not sure where you're going with this. There are notions of "higher categories" (e.g., bicategories) already out there, which serve to reflect the loosening of the condition of associativity of composition. So why not work directly with formalizing those extant notions, instead of redefining "category"?
Possibly I am misunderstanding your proposal, but in any case I think redefining category theory would result in great terminological confusion; call it by something else. I'm all for formalizing higher notions of category, though.
-
- CommentRowNumber15.
- CommentAuthorJonAwbrey
- CommentTimeOct 19th 2009
- (edited Oct 19th 2009)
Re: Jon, I think this is one of your less successful puns, since that's supposed to be a hard c in "principia".
Not to an old altar boy like me …
Anyway, it was supposed to be spin-off from our discussion of shells in the Cafe, since I sense a certain FOL-IE in trying to stuff any more math into the nutshell of FOL.
-
- CommentRowNumber16.
- CommentAuthorTodd_Trimble
- CommentTimeOct 19th 2009
Well, okay, but in that case wouldn't it be pronounced "princhipia"?
I was an altar boy too, but Episcopalians (in the 'low' form I grew up in, anyway) don't sing in Latin. I confess I don't know what the conventions were for Latin scholars in the time of Newton (which could for all I know be different in ecclesiastic Latin), but the hard c of course refers to Latin as originally spoken.
Do most people say "prinsipia"?
-
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeOct 19th 2009
<div> <blockquote> (The nlab page on n-category doesn't say anything about how important it is that the notion is weak! How did that happen?) </blockquote> <p>I felt for a long time that our entries on higher category theory were in bad shape given the role one would think they should play on the nLab. At one point I made an effort and spent a considerable bit of energy to expand <a href="https://ncatlab.org/nlab/show/higher+category+theory">higher category theory</a> at least. But more such effort is needed.</p> <p>Here we have the other problem, of lots of sub-case entries. Even if <a href="https://ncatlab.org/nlab/show/n-category">n-category</a> isn't exhaustive, at least <a href="https://ncatlab.org/nlab/show/infinity-category">infinity-category</a> should be.</p> </div> -
- CommentRowNumber18.
- CommentAuthorJonAwbrey
- CommentTimeOct 19th 2009
- (edited Oct 19th 2009)
Newton? Hecuba, no, I was talking about Russell.
I see you're a bit more punctilious about your puns than the pun of the mill I grind out.
I guess it all depends on how much wine the boys've been cippin' …
Goodbye, Mr.
-
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeOct 19th 2009
Jon,
in any case, I have to say that out of the majority of your comments here I am not able to extract the message that you might want to transmit. Maybe that's my fault, but even then.
It's probably fun to keep throwing around inside jokes once we are all inside one and the same context, indeed. But it doesn't seem we are. Let's try not to overburden a young forum still in its development.
-
- CommentRowNumber20.
- CommentAuthorTobyBartels
- CommentTimeOct 19th 2009
I strongly second Urs's request to have Todd and Toby's replies worked into an nLab page which has an explicit link to Mike's paper
I'll keep this page up and see if I can't write an article dedicated to the various possible formalisations and definitions of category (and functor and natural transformation). In case somebody else wants to write one, I'll make another note here before I actually start work.
Not to an old altar boy like me …
I pronounce it /princhipia/, since I assume that that's how Newton pronounced it, if not also Russell. I have no doubt that both of them learnt Latin with soft ‘c’s, whether more like /s/ or /sh/ I don't know; the contemporary practice of commonly teaching Latin with authentic classical pronunciations is less than a century old in the English-speaking world.
-
- CommentRowNumber21.
- CommentAuthorStephenGaito
- CommentTimeOct 20th 2009
Mike and Todd,
I have gone on yet another walk through most of the higher category pages that you both mention, as well as (re)reading (the initial parts of) Dominc Verity's Complicial Sets paper and I have to come to the same conclusion that I have come to before.... which is... my particular problem (time-series reconstruction) tells me (no robust mathematical definition of "tells" is known to me) that the current definitions of higher category theory are overly complex. More critically for me, my problem also tells me that bi- and 2-categories as well as category enrichment (at least as I read it in Dominc's paper: observations beginning at 10) are overly-rigid.
I realize that the following will may not be familiar to most of you, but most studies of Cellular Automata (CA) are done on "rigid" n+1 lattices (typically 1+1), however "reality" is "closer" to doing 1+1 CA's over Penrose quasi-periodic tilings of the plane. The distinct difference between these two examples is that one (over rigid lattices) has an "artificially-imposed" notion of the distinction between time and space, while the "more realistic example" (over Penrose tilings) has no such distinct separation (every "move" in "time" has a spacial component to it, conversely every "move" in "space" has a causal-time component to it). I realize that at the moment it is very far from obvious that this example has any applicability to Category Theory. I hope that, when the dust settles (some day), it will be seen to be a key example.
Suffice it to say, as I see it, the definitions of both bi- or 2-categories have a very similar "rigid" distinction between "horizontal" and "vertical" "arrows". My problem comes equipped with no such distinction. I believe that, when I pass to the appropriate limit, such distinctions will "appear", but that, at any approximate resolution, horizontal and vertical are all jumbled up together, in much the same way that time and space are jumbled in 1+1 CA's (finite approximations to physics) over a Penrose tiling.
The key aspect of my problem (and the thing no one that I know of does well) is to reconstruct a knowledge of "space" from a time series sampled at a "point". However this is exactly what even the lowliest of, for example, mammals can do. How do they do this? My problem tells me that it is done by keeping track of the spacial structure of a series of approximate Markov structures. When you take these approximate Markov structures to the appropriate limit, you naturally get a topological groupoid (category). But most importantly, to define the Markov structure in space-time you need spacial integrals. Since we are "naturally" working in a categorical setting, I believe, these integrals will turn out to be higher dimensional "Feynman integrals" over higher categorical hom-sets. That is they are integrals over the different ways of relating the lower categorical objects. I believe, that one of the reasons Feynman path integrals are rarely convergent, is due to the fact that we, currently, accidentally, ignore the higher categorical ways of relating the 1-simplicial histories in Feynman's path integral. (This is similar to what, in the theory of Bayesian networks, is referred to as the loop problem; see, for example, Chapter 5 section 3.5 of Pearl's Probabilistic Reasoning in Intelligent Systems).
Please rest assured that when the dust settles, what we currently call Category Theory will be natural specializations of what I want to call ((Transfinite) Simplicial) Category Theory. In particular any 1-simplicial Category (the current definition) will be naturally embed-able into any $\alpha$-simplicial Category (where $\alpha$ is "small-set" ordinal for which $1 < \alpha$).
Alas, I see that I need to progress my definition (even if it turns out that the current definitions of higher Categories have always been good enough for my needs) so that we can all see more of what I think I see.
-
- CommentRowNumber22.
- CommentAuthorJonAwbrey
- CommentTimeOct 20th 2009
- (edited Oct 20th 2009)
You are certainly playing out a number of different themes there.
As far as primitive models of learning go, I did spend one of my parallel lives getting a Master's in Psych, and part of what I did for that is to write a program for 2-level formal language learning that operated on ideas from Thorndike (law of effect + law of practice) and Guthrie (1-shot learning). Not that I was especially behaviorist or anything, but simply because that was the first step in trying program anything more complex.
Learning sequences of features in a Markov way is more or less the same thing as learning regular languages. Getting up to context-free languages is quite a bit harder — it requires a capacity for abductive reasoning, that is, making hypotheses and testing them against the data stream.
-
- CommentRowNumber23.
- CommentAuthorMike Shulman
- CommentTimeOct 20th 2009
So far I don't really see what you mean, but it is true that there's quite a zoo of higher-dimensional categorical structures in addition to n-categories. For instance there are double categories, triple categories, and n-fold categories, categories enriched over double categories, equipments, multicategories, higher multicategories, F-categories, lax-Gray categories, etc.
I suggest you develop your ideas and come up with a formal definition, continuing to pay attention to whether other people have defined similar notions in the past. You'll make people less unhappy, though, if you don't try to redefine words that have existing meanings, but rather come up with a new name for your new concepts. Finally, "Category Theory" is the name of a field of study, and is more general than any particular definition: it includes the study of categories, n-categories, double categories, etc. and will probably also include whatever notions you settle on.
-
- CommentRowNumber24.
- CommentAuthorStephenGaito
- CommentTimeOct 22nd 2009
Jon:
Learning sequences of features in a Markov way is more or less the same thing as learning regular languages. Getting up to context-free languages is quite a bit harder — it requires a capacity for abductive reasoning, that is, making hypotheses and testing them against the data stream.Indeed. Categories have associated (Categoric) symmetry actions (think Gauge theory). As an engineer if we make appropriate use of these actions we can seriously reduce the "size" of the (almost) Markov structures needed to "encode" "reality". Attention is the "motor" (frontal) part of the cortex operating on the "sensory" part of the cortex to implement just these actions for exactly this reason (brains are expensive (roughly 25% of the energy we consume each day goes to keeping our brains running).... so you DO NOT want more neurons than are really needed). The critical problem is understanding how the learning in the sensory and motor cortices differ. Abductive reasoning is the "motor" part of the cortex learning how to stabilize the "sensory" "signature" of "useful" "objects" in "reality". Couple in Markov Decision theory (aka Reinforcement Learning such as described by Sutton and Barto) with the theory of a few other neuroscience labs.... and I think you get a well engineered theory of the brain. Alas for me the first (and just the first) critical step is getting the Category theory correct.... (I wish I had 48 hour days and nothing else to do).
Mike:
I suggest you develop your ideas and come up with a formal definition, continuing to pay attention to whether other people have defined similar notions in the past.Again, indeed. When the dust settles, the current definitions will find natural places in the (Transfinite) Simplicial Category Theory that I am trying to define.
I am very sure that I do not know half of the Categoric "folk lore" (or even half the theory) that I should know to do what I need to do.
SO, I would be deeply honoured if, when I get an initial workable draft, nForum/nLab people read my draft and suggest where I should go to quote the relevant ideas which are not really new. I have more than enough to do, so I really do not want to redevelop everything from scratch if I can get away with a simple quote.
When I get to the point of having a useful draft, I will post a link to it on the nForum.
Many many thanks for all of your collective comments!
-
- CommentRowNumber25.
- CommentAuthorJonAwbrey
- CommentTimeOct 22nd 2009
- (edited Oct 22nd 2009)
McCulloch thought that abductive reasoning occurred in the Reticular Formation (RF), if I recall — see the papers collected in Embodied Mind. Early work on the link between Context-Free Languages and Push-Down Automata made explicit use of language about hypothesis testing, where the available hypotheses were represented by the non-terminal symbols.
The learner I wrote never got that smart — I got a Master's out of it but never got around to documenting the program in full. I made another stab at documentation and exposition a few years back, and what I've done so far is currently in this web neighborhood:
1 to 25 of 25