nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorEric
- CommentTimeOct 20th 2009
<div> <p>I added a statement to <a href="https://ncatlab.org/nlab/show/finite+category">finite category</a> that needs blessing by the experts.</p> <blockquote> For any <a href="https://ncatlab.org/nlab/show/finite+category">finite category</a> <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align: -20%;" class="tex" alt="C"/>, there is a <a href="https://ncatlab.org/nlab/show/directed+graph">directed graph</a> <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align: -20%;" class="tex" alt="G"/> such that its <a href="https://ncatlab.org/nlab/show/quiver">quiver</a> <img src="/extensions/vLaTeX/cache/latex_488df68f0543043cfe8c6e7d68900662.png" title="Q(G)" style="vertical-align: -20%;" class="tex" alt="Q(G)"/> is equivalent to <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align: -20%;" class="tex" alt="C"/>. </blockquote> <p>I wanted to say "is equal to" but was scared in this crowd :)</p> </div> -
- CommentRowNumber2.
- CommentAuthorEric
- CommentTimeOct 20th 2009
- (edited Oct 20th 2009)
One of the reasons for me to add this is that I wanted to think about a functor
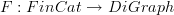
that forgets morphisms that are composites and keeps only those morphisms that cannot be written as a composite with some other non-identity morphism. These composite morphisms can be recovered from the graph by constructing its quiver. In other words, given a finite category, I want the smallest graph whose quiver is equivalent to the original finite category.
By the way, are there nontrivial endomorphism allowed in a finite category? If a non-identity endomorphism
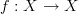 is in a finite category, then so is
is in a finite category, then so is 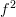 and
and 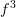 etc leading to an infinite number of morphisms. So to keep things finite, it seems you cannot have endomorphisms. Is that correct? What about if
etc leading to an infinite number of morphisms. So to keep things finite, it seems you cannot have endomorphisms. Is that correct? What about if 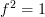 ? In other words, if
? In other words, if 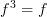 , are they considered different morphisms?
, are they considered different morphisms?Thanks!
-
- CommentRowNumber3.
- CommentAuthorTobyBartels
- CommentTimeOct 20th 2009
Mike and I have demolished your hopes back at finite category, but your motivation is still interesting. The usual forgetful functor
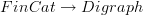 remembers all arrows and simply forgets the commutative diagrams, but one certainly could consider your functor that remembers only objects and ‘irreducible’ arrows. I think that, for a finite category, it's still true that the original category is a quotient of the quiver of this digraph, even though (thanks to nontrivial commutative diagrams) it will usually not actually be equivalent to that quiver.
remembers all arrows and simply forgets the commutative diagrams, but one certainly could consider your functor that remembers only objects and ‘irreducible’ arrows. I think that, for a finite category, it's still true that the original category is a quotient of the quiver of this digraph, even though (thanks to nontrivial commutative diagrams) it will usually not actually be equivalent to that quiver.You can nontrivial endomorphisms in a finite category, but they must satisfy some nontrivial equation
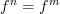 , such as
, such as 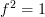 or
or 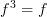 (which is weaker). Thus, if a digraph has loops, then its quiver will not be a finite category, although some quotients may be.
(which is weaker). Thus, if a digraph has loops, then its quiver will not be a finite category, although some quotients may be. -
- CommentRowNumber4.
- CommentAuthorEric
- CommentTimeOct 20th 2009
Thanks! I moved my "statement" to a "query".
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeOct 20th 2009
There is something close, though: for every category there is a poset such that both are equivalent in the Thomason model structure (do we have an entry on that). Meaning: both have the "same" oo-groupoid as their Kan fibrant replacement.
-
- CommentRowNumber6.
- CommentAuthorEric
- CommentTimeOct 20th 2009
I wish I knew the path that takes me from where I am now to where I could understood that last statement gulp :)
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeOct 20th 2009
In words it means this:
you can take a category and then freely add weak inverses to all morphisms.
Meaning: to each morphism that is non-invertible you add a morphism going the other way, which is an inverse up to some new 2-morphism which you throw in, which is invertible up to a new 3-morphism and so ever on and on.
The result is an oo-category that is an oo-groupoid. And the statement is: up to equivalence of oo-groupoids, every oo-groupoid is obtained this way alreday when starting with a category that is a poset.
A poset is not quite a free category on a graph, but it is in a qay a category with very little structure. One way to say this precisely is to realize that it is a (0,1)-category, so hardly more than a set.
Now remember that posets are also the natural candidate for encoding (globally hyperbolic) pseudo-riemannian spaces by abstract nonsense. Then I guess you may like this.
-
- CommentRowNumber8.
- CommentAuthorEric
- CommentTimeOct 20th 2009
- (edited Oct 20th 2009)
I like it I like it. I just wish I understood it better :)
Let me try to retype what you wrote to see if I get it.
Start with a poset. For each morphism, add a morphism that is inverse up to 2-morphisms that are invertible up to 3-morphisms that are invertible up to 4-morphism etc etc.
We end up with an oo-groupoid.
Not only that, but EVERY oo-groupoid has a poset at its heart for which this construction reproduces that oo-groupoid.
Is that primordial poset unique? Given an oo-groupoid, is it possible to extract this poset?
That does sound fascinating, but I'm sure I'm at least partially confused.
-
- CommentRowNumber9.
- CommentAuthorTobyBartels
- CommentTimeOct 20th 2009
Not only that, but EVERY oo-groupoid has a poset at its heart for which this construction reproduces that oo-groupoid.
That's not what Urs said, however. He said that every oo-groupoid that has a category at its heart for which this construction reproduces that oo-groupoid also has a poset at its heart for which this construction reproduces that oo-groupoid. But there may be yet other oo-groupoids. (Is there a clear counterexample, Urs?)
-
- CommentRowNumber10.
- CommentAuthorEric
- CommentTimeOct 21st 2009
- (edited Oct 21st 2009)
Is there some kind of "adjoint" that goes the other way? Instead of starting with a category and constructing an oo-groupoid, could you construct an oo-category from an oo-groupoid?
I am thinking of diamonation. If we start with a simple groupoid
we might construct a directed cylinder
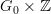 and force each morphism to require one "tick" of the discrete clock. We'd get a category which is an infinite criss cross ladder pattern with no real inverses. If that makes any sense.
and force each morphism to require one "tick" of the discrete clock. We'd get a category which is an infinite criss cross ladder pattern with no real inverses. If that makes any sense.I think of groupoids as "spaces" and categories as "spacetimes" so taking a category and constructing a groupoid, to me, feels like "projecting from spacetime down to space along time".
I'm interested in the opposite of extruding a space into spacetime by forming a directed cylinder.
-
- CommentRowNumber11.
- CommentAuthorMike Shulman
- CommentTimeOct 21st 2009
It is true that every ?-groupoid can be generated by freely adding inverses to a category. That's the content of the Quillen equivalence between Thomason's model structure for categories and the standard model structure on simplicial sets.
However, I'm actually not sure whether I believe that posets suffice. I've heard this quoted before, but I believe the justification is that Thomason claims that all the cofibrant objects in his model structure are posets, whereas I've also heard that there is an error in that argument. I haven't read it carefully myself.
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeOct 21st 2009
Thanks, Mike.
After I posted this yesterday I thought to myself: what actually is a reference for the poset statement? I know this statement from hearing it from people who should know.
Hm, our entry Thomason model structure could be slightly more detailed... :-)
-
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeOct 21st 2009
re Eric's question:
certainly what you indicate is a valid operation: you can take any oo-groupoid and take its cartesian product (as (oo,1)-categories) with some poset (say that of integers, which you indicated) to get an (oo,1)-category whose morphisms are generated from those that are part of the original oo-groupoid and those that "increase poset time", if you wish.
I'd think it is also generally posisble then to throw out those morphism that don't "increase poset time". i.e. all cartesian products of an oo-groupoid morphism with a poset identity morphism. This is what you have in mind.
But right this moment I can't quite seem to think of a nice abstract way to say this. Hmmm.
-
- CommentRowNumber14.
- CommentAuthorEric
- CommentTimeOct 21st 2009
I left a question about "walking commutative square" at finite category. -
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeOct 21st 2009
I added a - supposedly helpful - remark to the discussion at finite category.
-
- CommentRowNumber16.
- CommentAuthorEric
- CommentTimeOct 22nd 2009
I added some figures and some more thoughts. I think I'm starting to understand some things. Thank you!
-
- CommentRowNumber17.
- CommentAuthorTodd_Trimble
- CommentTimeOct 22nd 2009
Added some more comments on top of what Eric put down.
-
- CommentRowNumber18.
- CommentAuthorTobyBartels
- CommentTimeOct 22nd 2009
I'd think it is also generally posisble then to throw out those morphism that don't "increase poset time". i.e. all cartesian products of an oo-groupoid morphism with a poset identity morphism. This is what you have in mind.
You can't quite throw out all pairings (not 'products'!) of an
 -groupoid morphism with a poset identity morphism, since you must keep the pairings of identity
-groupoid morphism with a poset identity morphism, since you must keep the pairings of identity  -groupoid morphisms with identity poset morphisms, which are the identity morphisms in the resulting
-groupoid morphisms with identity poset morphisms, which are the identity morphisms in the resulting  -category.
-category.But notice that this is evil; applying this to equivalent
 -groupoids may lead to inequivalent
-groupoids may lead to inequivalent  -categories. In particular, Eric's original
-categories. In particular, Eric's original  -groupoid is contractible (equivalent to the point), yet the resulting
-groupoid is contractible (equivalent to the point), yet the resulting  -groupoid is not equivalent to the poset of integers.
-groupoid is not equivalent to the poset of integers.I see two ways to deal with this:
- Accept it; this means that you are not really starting with a space up to weak homotopy equivalence but instead a space equipped with a collection of points to take as the objects of a semistrict
 -groupoid.
-groupoid. - Keep the pairings that Urs said to throw out. Then Eric's directed cylinder will have a bunch of horizontal arrows as well as the diagonal ones. And if you start with a contractible space, then the resulting
 -groupoid is equivalent (as a weak
-groupoid is equivalent (as a weak  -groupoid) to the poset
-groupoid) to the poset 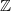 itself.
itself.
-
- CommentRowNumber19.
- CommentAuthorEric
- CommentTimeOct 22nd 2009
- (edited Oct 22nd 2009)
I wouldn't mind horizontal morphisms if they were pairings of identity morphisms. Does that help?
The important thing I'd like to maintain is that each non-identity morphism of the original category should "advance the clock" by one tick in the new category. It is ok (and expected) that identity morphisms in the original category do not advance the clock.
PS: Think zitterbewegung.
-
- CommentRowNumber20.
- CommentAuthorTobyBartels
- CommentTimeOct 22nd 2009
I wouldn't mind horizontal morphisms if they were pairings of identity morphisms. Does that help?
Not with the evil.
It's a good thing that you don't mind horizontal morphisms if they're pairings of identity morphisms; if you want an
 -category at all, then you must have identity morphisms, so you've got no choice about that! It's the nonidentity horizontal morphisms that are the problem.
-category at all, then you must have identity morphisms, so you've got no choice about that! It's the nonidentity horizontal morphisms that are the problem.If I understand your vision, you really need to take my first option (accept it); then you're not really starting from a space (up to weak homotopy equivalence) or an
 -groupoid (up to equivalence) but something like a semistrict
-groupoid (up to equivalence) but something like a semistrict  -groupoid up to some strict notion of equivalence (semistrict equivalence?).
-groupoid up to some strict notion of equivalence (semistrict equivalence?).In particular, if you happen to start with a groupoid, then you care about it up to isomorphism, not just up to equivalence.
-
- CommentRowNumber21.
- CommentAuthorEric
- CommentTimeOct 22nd 2009
- (edited Oct 22nd 2009)
To make things simpler, I'm happy to confine attention to groupoids with a finite number of objects if that helps.
One thing I might try is to "forget all non-trivial inverses", i.e. pick a non-identity morphism and remove its inverse. Continue until no non-identity morphism has an inverse. This is a category (Edit: We probably need to be more careful when deleting morphisms to make sure that the result is still actually a category, but that shouldn't be hard to do.) and I think we can recover the original groupoid via Kan fibrant replacement.
If this category is finite (which I'm happy to confine attention to), then we can find a directed
 -graph that recovers this finite category (in the way I'm trying to work out at finite category).
-graph that recovers this finite category (in the way I'm trying to work out at finite category).So we've effectively gone from a groupoid to directed graph. I'm also happy (Edit: No so sure I'm happy about this on second thought.) to confine attention to finite categories in which all paths commutes (is that a preorder?).
NOW, we can construct the cyclinder
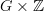 . THEN perform the operation of moving the target of each morphism up one time step. Reinsert morphisms from the target of each old morphism to the source of the old morphism, but UP one more time step so that the round trip along a morphism and its "inverse" requires TWO time steps. THEN, we can form the quiver of THIS graph.
. THEN perform the operation of moving the target of each morphism up one time step. Reinsert morphisms from the target of each old morphism to the source of the old morphism, but UP one more time step so that the round trip along a morphism and its "inverse" requires TWO time steps. THEN, we can form the quiver of THIS graph.I wonder if that gives you anything interesting? :)
I think that if we do this, then we could project the category down along
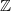 to recover the original groupoid.
to recover the original groupoid. -
- CommentRowNumber22.
- CommentAuthorTobyBartels
- CommentTimeOct 22nd 2009
So we've effectively gone from a groupoid to directed graph.
Again, you've done this in an evil way; you've really gone from a strict groupoid to a directed graph. That's OK, as long as you really care about your groupoid up to isomorphism and not just up to equivalence; it's just that, if you think of your groupoid as coming from a space, you must be caring about more than the space's weak homotopy type.
confine attention to finite categories in which all paths commutes (is that a preorder?)
Yes, it is precisely a finite preorder.
I've also got a new comment at finite category.
-
- CommentRowNumber23.
- CommentAuthorUrs
- CommentTimeOct 24th 2009
- (edited Oct 24th 2009)
Eric,
I just lookeed at the entry again: maybe you could change one of your graphics, then all four would be correct and could usefully be moved out of the discussion section into the main entry, or the entry on quiver:
namely the figure labeled "1-quiver" isn't quite right. The equality sign in the middle should be an inequality sign. Currently what is depicted is the "walking commuting square" which is not a free category.
We should also beware that we here are probably the only people in the world who systematically use "quiver" as a synonym for "free category". I think this is well justied by the way quivers are actually used. Instead of talking abut quivers, people ought to be talking about free categories! But I am not sure if that implies that we should coversely say quiver for a free category. I would prefer not to say quiver much at all.
Finally, concerning higher free categories, there is a bit of blog disucssion at freely generated omega-categories about that (which is synonymously related to the computads that Todd mentions in the discussion section at finite category).
-
- CommentRowNumber24.
- CommentAuthorTobyBartels
- CommentTimeOct 24th 2009
I don't like the term ‘free category’, because by default I expect that to mean the free category on a set (which is a discrete category). I would either say ‘free category on a graph’ (meaning a directed pseudograph as my version of graph, hopefully clear from context) or, of course, ‘quiver’.
-
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeOct 24th 2009
Right, free category on a graph.
-
- CommentRowNumber26.
- CommentAuthorMike Shulman
- CommentTimeOct 24th 2009
I don't like the term ‘free category’, because by default I expect that to mean the free category on a set
That's interesting; I don't expect that. Free categories on sets are fairly uninteresting, and besides we already have a word for them, namely "discrete." I would expect "free category" to mean the clearly more interesting and useful notion of a free category on a directed graph.
-
- CommentRowNumber27.
- CommentAuthorTobyBartels
- CommentTimeOct 24th 2009
I guess when I see the word ‘free’ I just take it to have a standard meaning (albeit relative to some forgetful functor to
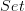 , but that's usually obvious) rather than one that depends on what is interesting and useful.
, but that's usually obvious) rather than one that depends on what is interesting and useful. -
- CommentRowNumber28.
- CommentAuthorTodd_Trimble
- CommentTimeOct 24th 2009
It feels funny to me to say just "free category" rather than "free category on a ___", but my own default would be to take ___ = "directed graph". In general I think I might default to ____ = "set" only if the forgetful functor to Set is monadic, and otherwise default to whatever is the "most obvious" monadic functor lying around.
-
- CommentRowNumber29.
- CommentAuthorMike Shulman
- CommentTimeOct 24th 2009
I guess when I see the word ‘free’ I just take it to have a standard meaning (albeit relative to some forgetful functor to Set, but that's usually obvious)
Of course, there are multiple forgetful functors from Cat to Set. We can take a category to its set of objects, or to its set of morphisms, or even to its set of isomorphism classes of objects. It's not clear to me that the first is more obvious than the others. The second one has the advantage of being faithful.
I think I'm with Todd, that "free" defaults to me for the most obvious monadic functor lying around, and for me the functor from Cat to DiGraph is the most obvious monadic functor defined on Cat.
-
- CommentRowNumber30.
- CommentAuthorUrs
- CommentTimeJun 19th 2013
I am hereby moving ancient discussion that was had in the entry finite categiry from there to here.
– begin forwarded discussion –
Eric: Is the following statement correct?
For any finite category , there is a directed graph such that its quiver is equivalent to .
Mike Shulman: No, this is false. The “walking commutative square”
is a finite category which is not free on any directed graph.
Toby: The walking commutative triangle is an even simpler counterexample. Rather, we should say that any finite category is a quotient of some quiver; the nontrivial commutation relations (triangles, squares, etc) give us this quotient. But in fact, there is nothing special about finite categories here; every category is a quotient of the quiver on its underlying graph. So I think that the only point to be made here is that, for a finite category, the graph may also be taken to be finite, but even that is obvious since the underlying graph is finite.
Eric: Thanks! That is interesting. This reminds me of the universal differential envelope on a complete directed graph. Any discrete calculus is a quotient of the universal discrete calculus obtained by removing some edges.
Toby: Sure, there are lots of adjunctions that work this way. (I forget the precise adjective that I should put before ’adjunction’ here.)
Mike Shulman: If the “walking commutative triangle” means what I think it does, then it actually is a quiver. The hypotenuse is freely generated as the composite of the other two sides.
- Toby: Erm … right. It's still a quiver; it's just not the quiver of the graph that I was thinking of! Sorry about that.
Eric: Wait a second. Does the “walking commutative square” consist of 4 objects? If so, then the diagonal should be a morphism because it is the composite of two sides so the diagram is not complete as drawn. It should include the diagonal. I’m sure I’m confused. What am I missing?
Mike Shulman: Yes, the diagonal is a morphism. I didn’t draw it because we don’t usually draw the diagonal when we draw a commutative square, just like we don’t usually draw identity morphisms.
Eric: Ok. I thought the missing diagonal was the barrier to being “free”. What is the barrier then? If you start with a directed graph as you drew without the diagonal then the corresponding quiver contains the diagonal as it should. There must be something else I’m missing. Thanks.
Urs Schreiber: apart from looking at the counterexample that Mike gave, it shoud be useful to say in words in full generality what is going on:
In a free category on a directed graph composition of morphisms is always just a concatenation operation. Nothing really happens when you compose any two morphisms.
So another good counterexample to think of is a delooping category of a monoid or of a group : in as far as the product operation in and actually does something instead of just saying that is , the corresponding category is not a free category.
Eric: I’m still confused. What is it about these counterexamples that make them counterexamples? For example, if is finite, then there is a finite number of elements that generate all of . We can construct a graph with one node and directed edge for each generator. Wouldn’t the resulting quiver be equivalent to ?
- Toby: It would if and only if is a free group generated by the elements . (And in that case, it would not be a finite category, except in the degenerate case where there are no elements at all.)
Mike Shulman: The point is that in the free category on the directed graph
there are two diagonals, one being generated by the top-right composite and the other by the bottom-left composite. If you included the diagonal itself as a generator in the directed graph, then there would be three diagonals.
– continued in next comment –
-
- CommentRowNumber31.
- CommentAuthorUrs
- CommentTimeJun 19th 2013
- (edited Jun 19th 2013)
– continuation of forwarded discussion –
Eric: Thanks Mike. That is very helpful. So given JUST a square graph, it’s quiver will have TWO diagonals. So we need more information. We need to specify something like a “curvature” that tells you how paths having the same start and end points fail to commute. When that curvature is zero, the paths commute.
If we label the directed edges ,,,, then when we construct the composites (to form the quiver) we end up with two diagonal morphisms and . We need a 2-morphism . To specify a rule for this 2-morphism, we probably need a 2-edge. In the absence of specifying a directed 2-edges, we could assume the curvature is flat. What this means is that we could have a concept of a “free -category” generated by a directed -graph. If there are no edges above , then it means all closed -paths commute.
This is a slightly different definition of a quiver where closed paths are assumed to commute. If you want a close -path to NOT commute, you need to specify a corresponding -edge connecting the two paths.
In other words, I think I’m suggested that we have free categories generated by a directed graph default to having all closed paths commute. If you want a closed path NOT to commute, you need to specify a 2-edge and form a 2-quiver. Does that make any sense?
Here are some pictures. Let’s say we start with a 2-graph square and form a “2-quiver” as illustrated below:
The 2-edge tells us that the composites and are not the same.
If we fail to include a 2-edge and start with the 1-graph and form its 1-quiver as illustrated below:
then it is as if we HAD included a 2-edge, but it is a trivial 2-edge and its corresponding 2-morphism is simply a 2-identity and the two composites commute.
I think that any finite category can be obtained in this way not via a finite 1-quiver (in which all closed 1-paths commute) but rather by a 2-quiver. If there is any sense to this, it seems to me to indicate that maybe a category with non-commuting paths is secretly a non-trivial 2-category somehow.
Todd: More examples of finite categories which are not quivers: take the group as a 1-object category. Or the category with two objects and exactly one morphism in each hom-set.
As far as your suggestion goes, I’m inclined to say you seem to have it backwards from how I’d go about it. There is a notion of something called “computad” which all this reminds me of, which come in various dimensional flavors. A 2-computad consists of a directed graph and a collection of “2-cells” or 2-edges whose source and target are directed paths in the directed graph (= morphisms in the free category on the directed graph). In my way of thinking, a 2-cell would provide something like a membrane or bridge or a homotopy which would allow you to identify paths (the source and target of the 2-cell) up to homotopy, instead of distinguishing them as you are doing. So, for any 2-computad, there would be something like its “fundamental category” (like a fundamental groupoid, but with directed paths considered modulo 2-cells), and you could say that any finite category is the fundamental category of some finite 2-computad. (But lots of different 2-computads would have the same fundamental category.)
There is also the notion of free 2-category generated from a 2-computad, and this is the beginning of an induction ladder.
Mike Shulman: Yeah, I’m with Todd; it seems strange to me to try to specify which diagrams don’t commute instead of which ones do.
I’m not sure if this is quite what you were thinking of with “a category with non-commuting paths [i.e. a category that isn’t a preorder] is secretly a non-trivial 2-category somehow”, but it’s not true that you can make a 2-category out of a category by putting a 2-cell between any two unequal parallel arrows. For one, there would be no identity 2-cells (since an arrow is equal to itself), and for two, you can’t compose inequalities; if and it can still be that .
David Roberts: I like the idea about the fundamental category of a 2-computad - I have some examples of things up my sleeve that I think this (and the next level up - the fundamental bicategory of a 3-computad) would very accurately describe. One of which is the localisation of a (small) category. Even more interesting for me would be the comparison with directed homotopy, especially if the 2-cells are not invertible.
– continued in next comment –
-
- CommentRowNumber32.
- CommentAuthorUrs
- CommentTimeJun 19th 2013
– continuation of forwarded discussion –
Eric: Thank you Todd and Mike! This is all very neat. That sounds interesting too David. I was also thinking about directed homotopy. I’m sure you guys are right and it is more natural to specify which diagrams commute rather than which diagrams don’t commute, but my motivation was curvature. If there is no curvature, then parallel transporting a particle along either path doesn’t matter. However, if there is curvature, then a particle will end up “rotated” depending on which path you take. In this analogy, it is the “absence” of curvature that makes the paths commute. It seemed natural that specifying a non-identity 2-edge was like specifying a non-zero curvature.
I like the idea of computads. I thought about that as well (although I didn’t know they were called computads), but I think you really can get away with just directed -graphs. Instead of a single directed edge as I drew in the picture which is more like a morphism between paths of length 2, we could have two 2-edges:
Then
is some kind of horizontal composition. Anyway, whether it is computads or directed graphs or specifying which edges commute or which edge don’t commute, I’m pretty excited. I’m much more comfortable thinking about directed graphs, so the more I can use them to help understand other concepts, the better for me. If finite categories can be reduced to some smaller atomic graph, that would be kind of neat.
Mike Shulman: I’m not sure what you mean by a 2-graph, but if you mean the obvious thing, then you can’t have an edge in one since and aren’t parallel.
By the way, I think the “fundamental category” of a computad is just going to be the reflection of its free 2-category into 1-categories (forcing all 2-cells to become identities). It’s certainly true that any finite category can be presented in this way by a finite computad, although not every category presented by a finite computad is finite (for instance, the monoid of natural numbers regarded as a 1-object category is presented by the computad with one object, one endo-1-cell, and no 2-cells).
Eric: Hi Mike. Here is the page on directed n-graphs. A directed 2-edge simply has a source 1-edge and a target 1-edge. These do not have to be parallel. If there is some problem with that, we should change the page. Any inaccuracies there are my fault :)
Todd Trimble: The notion of directed 2-graph as given there does seem weird to me. The problem is that if we think of a 2-cell as some kind of “shape” with boundary, then according to standard practice we should have something like “boundary of the boundary is zero”. In the computad setting, there are globularity conditions that say “source of the source = source of the target, and target of the source = target of the target” which give the boundary of boundary conditions.
Ultimately we would want some sort of geometric realization of these critters, and it’s hard to see how that would go precisely with the current directed n-graph.
Eric: One of the motivations (for me anyway) for that definition was precisely to get away from the globularity conditions. I come from the perspective of computational physics where the graph is intended to represent a model of spacetime. These types of directed -graphs are precisely what appear in our paper. I kind of think of them as being “pre-geometric”. They become geometric once you form the -quiver OR construct a differential graded algebra from them as Urs and I outlined in that paper.
In our paper, we start with just a directed 1-graph and build up the higher degree elements by introducing a coboundary. I agree, it is not “geometry” until you have a nilpotent coboundary, but these directed -graphs form the basis for building geometries.
You might sense I have aspirations for this stuff. Talking about “pre-geometry” in the hopes it might pertain to “primordial”. Something along the lines, “In the beginning, there was a graph…”
– continued in next comment –
-
- CommentRowNumber33.
- CommentAuthorUrs
- CommentTimeJun 19th 2013
– continuation of forwarded discussion –
Eric: It was starting to get late last night and I crashed, but kept thinking about this. Mike said:
it’s not true that you can make a 2-category out of a category by putting a 2-cell between any two unequal parallel arrows. For one, there would be no identity 2-cells (since an arrow is equal to itself),
Sorry I wasn’t clear. There are always identity 2-morphisms when you pass to the free category. The absence of a cell in the graph maps to an identity morphism in the quiver. That is why all 1-paths commute by default, i.e.
Each 1-edge gets mapped to a morphism PLUS an identity 2-morphism (and identity 3-morphism, etc). An edge is a trivial path that commutes with itself, which means each edge comes with an identity 2-morphism when passing to the guiver. This is completely analogous to how an -category can be thought of as an -category where all morphism greater than are identity morphisms.
I should have made that more clear.
and for two, you can’t compose inequalities; if and it can still be that .
This is fine. We want to think of , , as -transports. If is not an identity, it means . If is not an identity, it means . HOWEVER, if is an identity, then . The neat thing about this, which is a feature, not a bug, is that when composing two non-identity 2-morphisms gives an identity 2-morphism, it means that the 3-morphism is an identity 3-morphism.
In other words, the fact that you can’t compose inequalities is fine. In the case that and , but , this implies that the 2-paths commute and the corresponding 3-cell is an identity (meaning the 3-curvature vanishes). In fact, that is the default behavior. If you wanted the 2-paths to not commute, you’d have to insert a directed 3-edge giving non-zero 3-curvature.
Toby: A couple of points. First, if you want zero curvature to mean that every diagram commutes (which seems plausible), then zero curvature means that you have a proset, not that you have a quiver. Todd's group is a good example of both a non-quiver and a non-proset. The walking parallel pair of arrows ( where the two arrows are not equal) is a quiver but not a proset. And Mike's walking commutative square is not a quiver but is a proset. (My epic fail, the walking commutative triangle, is both a quiver and a proset.)
Now, if you want nonzero curvature to be given by some sort of -morphism, you might want to consider a -category whose hom-categories are enriched over an interesting monoid such as . Then each parallel pair of morphisms, instead of having a (possibly finite) set of -morphisms between them, will have a number as -morphism between them (note I did not say a number of -morphisms between them). The number indicates that they are equal (so the diagram commutes); but a nonzero number indicates a failure of commutativity to some degree. The rule for composition is addition; if is and is , then must be (and is always , which works since ). Note that it is possible to have and but (that is, and are nonzero but is zero) since we are using ; that would not be possible using . (Of course, you could just as well use , , or even in place of , but perhaps appeals to your desire for discreteness.)
– continued in next comment –
-
- CommentRowNumber34.
- CommentAuthorUrs
- CommentTimeJun 19th 2013
– continuation of forwarded discussion –
Eric: I knew I should have put “’s on the word “quiver”. This going to sound strange, but I’d say that the “walking commutative square” is not a quiver, but IS a 1-quiver. What people generally refer to as a “quiver” would actually be (related to) a 2-quiver coming from a 2-graph where the 2-cells help designate non-commuting paths. All 1-paths commute in a 1-quiver. All 2-paths commute in a 2-quiver, but not all 1-paths commute in a 2-quiver.
Currently, I’m proposing that any finite category is obtained from the 2-quiver of some finite directed 2-graph by turning all 2-morphisms into identities (is there a term for a subcategory obtained by turning all -morphisms for greater than some number to identities?).
Toby: If you start with an -category and turn all -morphisms for into equivalences, then you get an -category that I would call the
__-core__of . (I just made up ‘-core’, but the -core is the ordinary core, which is an -category, that is an -groupoid). And if you then turn all of the -equivalences for into equivalences, then you get a -category which is (I am not making this up) the -truncation of the -core of . Probably people would be happy to call this the -truncation of itself, but now I am making up terms again, as far as I know. So in summary, if you turn all -morphisms for (note my subtle level shift here) into identities, then you get the -truncation of .Eric: Here is an attempt at something semi-formal:
+– {: .un_prop}
Proposition
A finite category is the 1-truncation of a free 2-poset for some Hasse 2-graph. =–
+– {: myproof}
Proof
??? =–
Mike Shulman: Eric, I’m very confused. Can you maybe use something other than “n-quiver” for whatever it is you’re trying to describe? In general we try to make a “1-foo” be the same as a “foo”.
Also, as I said at directed n-graph, I really don’t like that term; saying “-graph” automatically makes me think “-globular set”. Moreover, for purposes of freely generating -categories I think the extra generality of not requiring the globularity conditions is superfluous; the free functor from -nonglobular sets to -categories factors through -globular sets, so you might as well start with an -globular set.
Thirdly, I don’t think you have any hope of getting only finite categories this way; you’re always going to get some finitely presented categories that are not finite (like the monoid as a one-object category).
Toby, what I would call the “-core” is what you get by discarding -morphisms for that are not equivalences. Is that what you meant?
- Toby: No, I was just messed up. It was Eric who wanted to make all -morphisms into equivalences (and indeed identities), so the core is not correct.
Eric: Sure. Sorry about that. Until a better name is found, I think I’ll just call it a free n-poset. I’m trying to develop some ideas at Hasse n-graph. Toby and I were discussing this a bit here.
By the way, I’m not hoping to get only finite categories this way. My only hope is that I can find a way to obtain any finite category this way (or some way similar).
Mike Shulman: As I said at directed n-graph, it sounds like maybe you really want a computad. It is true that any (finite) category can be obtained as the 1-truncation of the free 2-category on some (finite) 2-computad; in fact this is more or less the definition of a “finitely presented category.”
I still don’t understand your response to me above (beginning with “Sorry I wasn’t clear”).
– end of forwarded discussion –
-
- CommentRowNumber35.
- CommentAuthorDavid_Corfield
- CommentTimeFeb 15th 2021
A better link to have from finite category is presumably to homotopy type with finite homotopy groups rather than finite homotopy type, no?
-
- CommentRowNumber36.
- CommentAuthorDavid_Corfield
- CommentTimeFeb 15th 2021
-
- CommentRowNumber37.
- CommentAuthorDavid_Corfield
- CommentTimeFeb 15th 2021
Shouldn’t there be some up-to-equivalence condition? Essentially finite?
1 to 37 of 37