Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology definitions deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nforum nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: Schur functors

Bottom of Page

1 to 10 of 10

  1.  
    • CommentRowNumber1.
    • CommentAuthorTobyBartels
    • CommentTimeOct 25th 2009

    Todd started Schur functor. I added internal links and wrote linear category to be the target of one of them.

    • CommentRowNumber2.
    • CommentAuthorTodd_Trimble
    • CommentTimeOct 25th 2009

    Thanks, but I should say that I was in the middle of an edit when you did all that, and my submission erased your links, which I tried to reinsert. Please check: the link to "change of base" was supposed to point to an extant page, but I'm not sure which.

    • CommentRowNumber3.
    • CommentAuthorTobyBartels
    • CommentTimeOct 25th 2009

    Ah, your edit took longer than 30 minutes, so the lock timed out! And here I thought that you had cancelled it.

    • CommentRowNumber4.
    • CommentAuthorTodd_Trimble
    • CommentTimeOct 25th 2009

    Ah, I had no idea that locks time out! That's annoying, but at least now I know. I was busy trying to get the kids in bed and so on when it happened.

    • CommentRowNumber5.
    • CommentAuthorTobyBartels
    • CommentTimeOct 25th 2009

    I believe that they time out so that people can't lock a page forever if they just forget about it or their Internet connection crashes or something.

    Sometimes I'll save a draft every 15 minutes or so to prevent it.

    • CommentRowNumber6.
    • CommentAuthorGuest
    • CommentTimeOct 26th 2009
    To get around the spam filter in the minimum time, I'll drop my intended comment for Schur functor here:

    is the divided powers functor Ab --> Ab a Schur functor? The preprint arXiv:0910.2817, section 2.1 has details.
    How about the Lie functor Ab --> Ab, which is just the tensor algebra with the obvious Z-Lie structure? Same paper for details.

    David Roberts
    • CommentRowNumber7.
    • CommentAuthorTodd_Trimble
    • CommentTimeOct 26th 2009

    Thanks, David. For the time being I'm restricting to categories enriched in rational vector spaces, so for the time being let me apply the query to 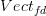Vect_{fd} (finite-dimensional spaces) instead of 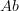Ab. Then yes, it looks like their paper gives formulas for the homogeneous components of these constructions as direct sums of certain classical 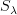S_\lambda's.

    • CommentRowNumber8.
    • CommentAuthorbwebster
    • CommentTimeOct 27th 2009
    I added a stubby part about using arbitrary representations of S_n.
    • CommentRowNumber9.
    • CommentAuthorTodd_Trimble
    • CommentTimeOct 27th 2009

    Thanks, Ben. I added a small and maybe slightly cryptic comment, to be followed up on later.

    • CommentRowNumber10.
    • CommentAuthorbwebster
    • CommentTimeOct 28th 2009

    I also created a stub on Specht modules, which should be key for defining analogues of Schur functors for all abelian monoidal categories.

1 to 10 of 10

  1.