Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nforum nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf sheaves simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: model structure on simplicial presheaves and related

Bottom of Page

1 to 13 of 13

  1.  
    • CommentRowNumber1.
    • CommentAuthorUrs
    • CommentTimeOct 28th 2009

    Over on MO Denis-Charles Cisinki kindly replied to some issues that I am recently working on here. See this.

    • CommentRowNumber2.
    • CommentAuthorUrs
    • CommentTimeOct 29th 2009
    • (edited Oct 29th 2009)

    now I re-instantiated at model structure on simplicial presheaves in the section "cofibrant objects" my proof that all degreewise coproducts of representables are cofibrant. (I had removed it after somebody pointed out that Dugger assumes an extra condition to prove this, which made me worry that I had an error in my reasoning).

    But before that I have included now the one order of magnitude shorter proof that Denis Charles-Cisinski pointed out (I still feel like keeping mine though... :-)

    • CommentRowNumber3.
    • CommentAuthorUrs
    • CommentTimeOct 29th 2009
    • (edited Oct 29th 2009)

    I keep oscillating. Now I realize that I don't understand Denis-Charles Cisinski's argument in detail after all.

    So I now put in a warning and a question query box back in here .

    • CommentRowNumber4.
    • CommentAuthorUrs
    • CommentTimeNov 7th 2009
    • (edited Nov 7th 2009)

    The situation is a bit nerve-wrecking:

    behind the scenes we have two people who should know: one of them argues that my claim that in the projective model structure on simplicial presheaves all degreewise representables are cofibrant is indeed correct and offers his own proof for it. The other one finds fault with this proof, though.

    But neither of them considers my proposed proof of this statement.

    But it wasn't written up nicely. I have now tried to considerably clean it up. It is at model structure on simplicial presheaves -- cofibrant objects.

    The way I approach this, it is really entirely an exercise in end/coend yoga, the input from model category theory needed is minimal.

    So maybe some cat theory wizards (Todd? Mike? Toby?) would like to check my reasoning. If I am making a stupid mistake it should be easy to spot for you. If my reasoning is correct, the resulting statement would be a quite useful technical statement improving the existant one in the literature (which is of course precisely what makes me nervous).

    • CommentRowNumber5.
    • CommentAuthorMike Shulman
    • CommentTimeNov 7th 2009

    I think I found a subtle error.

    • CommentRowNumber6.
    • CommentAuthorUrs
    • CommentTimeNov 9th 2009
    • (edited Nov 9th 2009)

    Thanks, Mike. I see what you mean.

    In the previous version of this attempt I had used instead the presentation 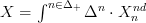X = \int^{n \in \Delta_+} \Delta^n \cdot X_n^{nd} of a simplicial set as a coend of only its non-degenerate cells over the category 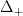\Delta_+ of injective order preserving maps, such as to not have to worry about the part where you now point out a mistake.

    But then I realized that it is not obvious that I can take an entire presheaf of simplicial sets and restrict it to non-degenerate cells objectswise. So when I rewrote it now I thought I could just as well use the full coend 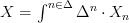X = \int^{n \in \Delta} \Delta^n \cdot X_n . But as you point out I cannot.

    Okay, thanks again. I have moved my wrong proof to the bottom of the page in a Disscussion section.

    • CommentRowNumber7.
    • CommentAuthorUrs
    • CommentTimeNov 10th 2009

    I added a section on cofibrant replacement

    model structure on simplicial presheaves -- cofibrant replacement

    This just states one of Dugger's cofibrant replacement functors and then has a query box. I keep staring at it but must be being silly again. Help is appreciated.

    • CommentRowNumber8.
    • CommentAuthorUrs
    • CommentTimeNov 10th 2009

    Oh, I see my mistake. Never mind.

    • CommentRowNumber9.
    • CommentAuthorUrs
    • CommentTimeNov 17th 2009
    • (edited Nov 17th 2009)

    added to local model structure on simplicial presheaves a warning that the general existence result of Bousfield localization does not apply, as the weak equivalences do not form a set, but a proper class.

    This is getting on my nerves, by the way, that so many concrete constructions depend on size issues in model category theory and in (oo,1)-category theory. In principle I can handle that, but whenever size issues come up I feel like the ground on which I am walking becomes more shaky.

    There was a related discussion recently on SBS. But can anyone maybe tell me again: how am I to think of the fact that size issues -- which usually one is inclined to react to by "doesn't matter, can be dealt with if desired" -- may become so crucial.

    Well, maybe I just don't get it yet after all: why don't we just say, for instance: Bousfield localization of combinatorial model categories exists always, if only we pass to a large enough Grothendieck universe?

    In physics discussion groups there is this recurring topic every once in a while: "Does anyone know of any physical aspect that depends crucially on set-theoretic subtleties?" Usually everybody shrugs and no example is given. But it's striking, once one realizes one needs model categories/(oo,1)-catgegories all over the place in physics, suddenly also set theoretic issues are there all over the place. Certainly nobody alerted me of that when I studied physics...

    • CommentRowNumber10.
    • CommentAuthorMike Shulman
    • CommentTimeNov 17th 2009
    • (edited Nov 17th 2009)

    why don't we just say, for instance: Bousfield localization of combinatorial model categories exists always, if only we pass to a large enough Grothendieck universe?

    Because it's not true. Changing your universe also changes the meaning of "combinatorial model category" and thereby preserves the largeness of the class of maps you may want to localize at.

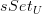    More explicitly, consider the category [C^{op},sSet] of simplicial presheaves on a site C with some global model structure, and some class W of weak equivalences one wants to localize at. If U is a universe (and C is U-small), it is true that the class W_U of weak equivalences in [C^{op},sSet_U] is a set, where sSet_U is the category of U-small simplicial sets. But [C^{op},sSet_U] is not a combinatorial model category. 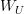(One could say that it's "U-small-combinatorial" meaning that "U thinks that it is locally presentable," but of course also "U thinks that W_U is a proper class" so that doesn't help.) The real combinatorial model category is now [C^{op},sSet], which can take values in not-necessarily-U-small simplicial sets, and in that category the class W of weak equivalences is not a set (even a U-large one). We could localize [C^{op},sSet] with respect to the set of maps W_U, but there's no guarantee that that would be the same as localizing at all of W.

    how am I to think of the fact that size issues -- which usually one is inclined to react to by "doesn't matter, can be dealt with if desired" -- may become so crucial.

    One possible answer would be that one's usual inclination can be wrong. (-: Some set theorist is fond of pointing out that even if it is true that ZFC suffices for all "real-world" mathematics and physics, Gödel's Incompleteness Theorem means that this will never be more than a description of the current state of affairs.

    However, I usually consider that size questions usually matter most when one wants to apply model-categorical techniques, and model categories are merely a technical tool (however ubiquitous and useful) rather than a fundamental notion. In the world of pure 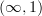(\infty,1)-categories, size questions should be much less important. (Though they may not be completely absent, neither are they completely absent from ordinary 1-category theory.)

    • CommentRowNumber11.
    • CommentAuthorUrs
    • CommentTimeNov 17th 2009
    This comment is invalid XHTML+MathML+SVG; displaying source. <div> <blockquote> Changing your universe also changes the meaning of "combinatorial model category" and thereby preserves the largeness of the class of maps you may want to localize at. </blockquote> <p>Right, thanks, Mike. I guess I follow this. It <em>still</em> annoys me, though. :-)</p> <p>But I would like to come back to your statements about the matter of size issues in categories and <img src="/extensions/vLaTeX/cache/latex_5b4e8bf1a57dcb0e372c2512e8f20c01.png" title="(\infty,1)" style="vertical-align: -20%;" class="tex" alt="(\infty,1)"/>-categories independent of models. What is really the right way to think of size issues in the context of accessible categories, presentabled categories, etc, if any?</p> <p>I see so much talk about foundational issues, and am hoping that one day out of all this comes an answer that I cannot only follow, but that <em>feels good</em> . A good answer to what is really going on. Not sure if i can express in words whjat i am really looking for. But somehow it feels as if in category theory everything is maximally nice, except that these darn size issues get in the way. Well, I suppose the answer is I should not fight it but embrace it, then it will also feel better...</p> </div>
    • CommentRowNumber12.
    • CommentAuthorTobyBartels
    • CommentTimeNov 17th 2009

    Remember, size issues are the only reason why there are complete categories other than complete lattices. So you should be grateful!

    • CommentRowNumber13.
    • CommentAuthorMike Shulman
    • CommentTimeNov 18th 2009

    To second what Toby said, I think that at some level it is just true that size issues do matter, and maybe you should "not fight it but embrace it". Sometimes size is an avoidable detail, but sometimes it isn't. The fact that it doesn't "feel good" to you might say more about your "feel-gooder" than about the mathematics. Not that it's wrong for you to not like size issues; it is of course possible and common for good and important mathematics to seem unaesthetic to particular mathematicians. For instance, I'm not fond of involved combinatorics or computations, and though sometimes those can be avoided by categorical tricks (one reason I like category theory), other times they seem to be unavoidable, even in good and important mathematics.

    I do admit to occasionally wishing that size issues could be dealt with more cleanly, though. Feferman set theory does this better than many other approaches, although it's a little too set-theoretically involved to have been widely adopted. This sort of feeling is also what motivated me to think about the possibility of a category of all sets (michaelshulman).

1 to 13 of 13

  1.