nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorMike Shulman
- CommentTimeNov 5th 2009
- (edited Nov 5th 2009)
Started writing regular and exact completion.
-
- CommentRowNumber2.
- CommentAuthorTobyBartels
- CommentTimeNov 6th 2009
Mike has added many interesting properties of these completions now.
-
- CommentRowNumber3.
- CommentAuthorMike Shulman
- CommentTimeNov 6th 2009
Do you know, I find myself thinking that an interesting argument against the powerset axiom is that unlike basically all the other logical/set-theoretic properties of categories, it is not preserved by the free ex/lex completion. Given that (in the absence of choice)
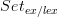 is not necessarily a topos, and in fact isn't even well-powered relative to the original category Set, it becomes philosophically less self-evident to me that Set itself should be a topos. Especially since from the type-theoretic defined-equality point of view, Set is itself an ex/lex completion (of the category of presets).
is not necessarily a topos, and in fact isn't even well-powered relative to the original category Set, it becomes philosophically less self-evident to me that Set itself should be a topos. Especially since from the type-theoretic defined-equality point of view, Set is itself an ex/lex completion (of the category of presets). -
- CommentRowNumber4.
- CommentAuthorTobyBartels
- CommentTimeNov 6th 2009
Ha ha, we'll make a predicativist out of you yet!
-
- CommentRowNumber5.
- CommentAuthorMike Shulman
- CommentTimeNov 8th 2009
I added some more properties of regular and exact completions, including that the ex/lex and reg/lex completions can never stabilize unless they do so in one step, and that they are Boolean if and only if the original category satisfies AC. I also added a higher-categorical perspective, and deleted the query box at regular category since its content was basically subsumed by my recent additions, and probably regular and exact completions would be a better place to continue it anyway.
-
- CommentRowNumber6.
- CommentAuthorTodd_Trimble
- CommentTimeJan 3rd 2010
- (edited Jan 3rd 2010)
I have some questions for Mike at regular and exact completions.
-
- CommentRowNumber7.
- CommentAuthorMike Shulman
- CommentTimeJan 3rd 2010
Good questions, I've answered them.
-
- CommentRowNumber8.
- CommentAuthorTodd_Trimble
- CommentTimeJan 4th 2010
Thanks at regular and exact completions.
1 to 8 of 8