nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber201.
- CommentAuthorEric
- CommentTimeApr 2nd 2010
The nLab says:
A diagram in a category
 is simply a functor
is simply a functor 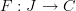 .
.The category
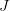 is called the shape or index category of the diagram, and is typically understood to be a small category.
is called the shape or index category of the diagram, and is typically understood to be a small category.Does
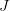 need to be a free category?
need to be a free category?If so, I think it would be helpful to explicitly state it like I did above:
Given a graph
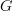 and a category
and a category  , a diagram in
, a diagram in  is a functor
is a functor 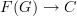 .
.A commutative diagram is a diagram
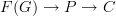 which factors through a preorder
which factors through a preorder 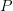 .
.This would be much clearer to me. What do you think? Can we change the nLab?
This would also lead directly to the statement:
A diagram may also be thought of (via adjunction) as a graph morphism
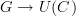 .
. -
- CommentRowNumber202.
- CommentAuthorHarry Gindi
- CommentTimeApr 2nd 2010
- (edited Apr 2nd 2010)
@Eric: I apologize if that came off a bit rude. It was not my intention.
The main problem that I see with using the "functors are maps of graphs" approach is that it is a lot more confusing and complicated. The real benefit from the diagram approach comes from things like limits and colimits, where the choice of index category only matters for the shape. However, in practice, it still feels a lot easier to just be careful with your definition of limit/colimit, which you can apply to arbitrary functors (provided they exist).
I prefer to reserve statements about commutativity to actual diagrams that I can draw (or at least pieces of diagrams, if they're infinite). All of these statements about posets etc are interesting, but we all have an intuitive notion of what it means for a diagram to commute. I submit to you that the notion of an abstract diagram as a map on graphs, let alone any definition of what it means for such a creature to commute, is certainly more difficult to work with than saying that a functor is a map on the set of objects and the set of arrows preserving identities and composition. Even if we want to use an unbiased definition, it's still the same. That is, we just say that F preserves n-ary composites for all n in N (notably including 0, where the 0ary composite at an object is the identity).
(By the way, defining the identity to be the 0-ary composite doesn't seem right, since the 0-ary composite does not have an explicit domain/codomain. This means that we have to define a notion of a 0-ary composite at an object, which is much less parsimonious than just splitting off the case of n=0.)
Edit: Eric, I am against changing the definition of a diagram. The whole beauty of the standard approach is not that we can describe categories as graphs, but that we can describe a diagram as a functor!
-
- CommentRowNumber203.
- CommentAuthorEric
- CommentTimeApr 2nd 2010
@Harry: No worries about that. The help you give more than makes up for things like that. Plus, I somewhat disagree with Todd. Being unfriendly towards engineers actually puts you in very good company in the mathematics community (present company excluded!) :)
As I mentioned before, since you are not a "scientist nor engineer", you do not have a say in what they find easier :) The most you can say is that it is easier for you and that is great. I've been around long enough and I've known enough "scientists and engineers" to say with some confidence that most would be much more comfortable working with graphs, since graphs pervade almost all scientific disciplines.
Besides, in my suggested modification to the nLab above, the functor aspect was front and center and was part of the definition. The relation to graph morphisms was secondary.
Or are you hesitant about using the word "graph" in the definition? If that is the case, then I'd disagree. I think it is perfectly acceptable for the word graph to appear in the definition of a diagram.
What I'd really like to know is whether my suggested modification is acceptable to the experts. Is it?
-
- CommentRowNumber204.
- CommentAuthorTodd_Trimble
- CommentTimeApr 2nd 2010
- (edited Apr 2nd 2010)
Eric: you could rephrase that way, but now that this discussion is at last converging toward consensus (yay!), I think the issue of whether to use free categories or not becomes a bit subsidiary and can be relegated to a comment.
In other words, you could define a diagram as we currently have it in the Lab, as a functor
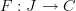 , and say the diagram commutes if it factors through a preorder
, and say the diagram commutes if it factors through a preorder 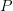 . (This
. (This 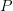 can be taken to be the preorder reflection of
can be taken to be the preorder reflection of 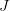 -- offhand I'm not sure where that would link to.) This uses a few less words than if you brought in free categories or whatever, and is somewhat more general. But I still think Mike's earlier words on this still have a certain legitimacy and deserve to be noted as a comment in the article.
-- offhand I'm not sure where that would link to.) This uses a few less words than if you brought in free categories or whatever, and is somewhat more general. But I still think Mike's earlier words on this still have a certain legitimacy and deserve to be noted as a comment in the article.I lean slightly toward the more general formulation, but either definition is okay with me; the definition you want to use Eric is certainly defensible. At this point I can bow out of the conversation. :-)
-
- CommentRowNumber205.
- CommentAuthorEric
- CommentTimeApr 2nd 2010
- (edited Apr 2nd 2010)
@Todd: Ok, but if
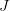 is not free, do we need to abandon the adjunction? I would like to be able to think in terms of graph morphisms, but in the more general case, would graph morphisms just be special cases?
is not free, do we need to abandon the adjunction? I would like to be able to think in terms of graph morphisms, but in the more general case, would graph morphisms just be special cases? -
- CommentRowNumber206.
- CommentAuthorTodd_Trimble
- CommentTimeApr 2nd 2010
Yes, that formulation doesn't mention that adjunction. Graph morphisms would be special cases. But those are the cases which generally arise in practice when we wave our hands and point to or draw commutative diagrams, as one can verify by opening just about any book. :-)
-
- CommentRowNumber207.
- CommentAuthorEric
- CommentTimeApr 2nd 2010
- (edited Apr 2nd 2010)
Hmm... I'm not a big fan of definitions like:
- A diagram is simply a functor
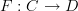 . Period.
. Period. - A representation is simply a functor
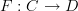 . Period.
. Period.
That makes me wonder, "Is a diagram simply a representation? Why have three words for the same thing?"
In this case, I probably would prefer to restrict things just a little unless there is a good reason not to. That way I can safely keep in the back of my head "a diagram is basically a graph morphism". This is what it means for all practical purposes.
Should we take a vote on it? :)
Thanks again everyone for your help. I just redrew my favorite example, but now starting with a graph
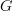 given by
given by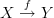
and a graph
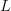 given by
given by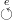 .
.From here we can construct the free category of the loop
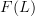 and project this back down to a graph
and project this back down to a graph 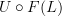 with one node and an infinite number of directed edges, one for each morphism
with one node and an infinite number of directed edges, one for each morphism 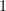 ,
,  ,
, 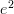 , etc.
, etc.A diagram is a graph morphism
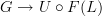 . Of course
. Of course 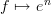 for some
for some 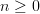 and there are no hidden identities etc forcing
and there are no hidden identities etc forcing 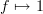 .
.Mystery solved :)
-
- CommentRowNumber208.
- CommentAuthorMike Shulman
- CommentTimeApr 2nd 2010
What about "A diagram is a functor. When we ask whether a diagram commutes, we are usually thinking only of diagrams whose source is the free category on a graph, in which case we say the diagram commutes iff it factors through the free preorder on that graph (or, equivalently, through any preorder). Note that by adjunction, a functor
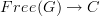 is the same as a graph morphism
is the same as a graph morphism 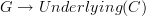 , i.e. a 'labeling' of the vertices and edges of G by objects and morphisms in C. This labeling is what we usually draw on the page when we talk about commutative diagrams."
, i.e. a 'labeling' of the vertices and edges of G by objects and morphisms in C. This labeling is what we usually draw on the page when we talk about commutative diagrams." -
- CommentRowNumber209.
- CommentAuthorTodd_Trimble
- CommentTimeApr 3rd 2010
That sounds good to me, Mike.
Eric, my own take is that different terms for (roughly) the same concept can convey slightly different senses or "moods" or emphases, just as in ordinary language use. For example, I would sooner say "a diagram in
 is a functor
is a functor 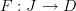 , where
, where 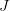 is small. A representation of
is small. A representation of  is a functor whose domain is
is a functor whose domain is  ." There's a difference in sense.
." There's a difference in sense. -
- CommentRowNumber210.
- CommentAuthorEric
- CommentTimeApr 3rd 2010
<p>I should go through these 200+ comments and pick out pearls of wisdom and add them to the nLab. That is a small project and, time permitting, I will do my best.</p> <p>But for now, I thought I would summarize some of the key mental stumbling blocks that I think point to ways we can improve the nLab to help future "scientists and engineers" avoid the same problems I had.</p> <p>First, although this probably sounds silly, one thing that really hung me up was thinking that the image <img src="/extensions/vLaTeX/cache/latex_dc3fcd71eea8cc9d58dab8ea82eae894.png" title="F(C)" style="vertical-align:-20%;" class="tex" alt="F(C)" /> was a subcategory of <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align:-20%;" class="tex" alt="D" />. This one factoid caused me immeasurable mental duress. This should be stated clearly somewhere on <a href="https://ncatlab.org/nlab/show/functor">functor</a> I think. Because of this, I thought every diagram was a category. This should also be repeated on <a href="https://ncatlab.org/nlab/show/diagram">diagram</a>, i.e. a diagram is not necessarily a subcategory.</p> <p>For instance, since a diagram does not need to be a category, we can have diagrams like this</p> <img src="/extensions/vLaTeX/cache/latex_4d662ed5ce56aeded1feedc49769df6f.png" title="\bullet\stackrel{e}{\to}\bullet" style="vertical-align:-20%;" class="tex" alt="\bullet\stackrel{e}{\to}\bullet" /> <p>without hidden antiparallel identity morphisms stretched between the two copies of <img src="/extensions/vLaTeX/cache/latex_2668009033d84cdc8d16f29c11ae03fd.png" title="\bullet" style="vertical-align:-20%;" class="tex" alt="\bullet" />. If this were a category, I would probably insist that there should be hidden antiparallel identity morphisms.</p> <p>Second, when talking about commuting diagrams, we are almost always talking about functors from a free category, in which case we can mentally switch to thinking about graph morphisms due to the adjunction. This is pretty cool. Commuting diagrams in terms of graph morphisms is something I think "scientists and engineers" could really internalize easily, so this gives a nice segue to adjunctions. For the record, I think most scientists and engineers can easily internalize commuting diagrams in terms of functors too as long as they avoid the trap of thinking a diagram has to be a category (like I did!).</p> <p>A part of me still wishes we could define a diagram as follows:</p> <blockquote> <p>Given a graph <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" /> and a category <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" />, a <strong>diagram</strong> in <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> is a functor <img src="/extensions/vLaTeX/cache/latex_0d1483327531dd4153e5ea333e6a3753.png" title="F(G)\to C" style="vertical-align:-20%;" class="tex" alt="F(G)\to C" />.</p> <p>A <strong>commutative diagram</strong> is a diagram <img src="/extensions/vLaTeX/cache/latex_09ac822acf7c1965b64c285756e7b0a9.png" title="F(G)\to P\to C" style="vertical-align:-20%;" class="tex" alt="F(G)\to P\to C" /> which factors through a preorder <img src="/extensions/vLaTeX/cache/latex_0827b2155898e7e29e51b4330f4c0e75.png" title="P" style="vertical-align:-20%;" class="tex" alt="P" />.</p> </blockquote> <p>I like this because diagrams are almost always (I can't think of a counter example) functors from free categories for some graph. Defining it this way allows the equivalent definition stated via the adjunction:</p> <blockquote> <p>Given a graph <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" /> and a category <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" />, a <strong>diagram</strong> in <img src="/extensions/vLaTeX/cache/latex_6b9aaf533fd24793040c8ec9ce302c75.png" title="U(C)" style="vertical-align:-20%;" class="tex" alt="U(C)" /> is a graph morphism <img src="/extensions/vLaTeX/cache/latex_27cc390aec1b1c61f926a3fbe835813e.png" title="G\to U(C)" style="vertical-align:-20%;" class="tex" alt="G\to U(C)" />.</p> <p>A <strong>commutative diagram</strong> is a diagram <img src="/extensions/vLaTeX/cache/latex_09ac822acf7c1965b64c285756e7b0a9.png" title="F(G)\to P\to C" style="vertical-align:-20%;" class="tex" alt="F(G)\to P\to C" /> which factors through a preorder <img src="/extensions/vLaTeX/cache/latex_0827b2155898e7e29e51b4330f4c0e75.png" title="P" style="vertical-align:-20%;" class="tex" alt="P" />.</p> </blockquote> <p>In fact, that last sentence could probably be improved, because I'm willing to bet that any preorder is a quiver for some graph, so it could probably be recast as a special kind of graph morphism.</p> <p>There is one more worry on my mind though...</p> <p>Back <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7112#Comment_7112">here</a>, I gave two definitions:</p> <hr /> <p><strong>Definition #1:</strong></p> <p>Given categories <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> and <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align:-20%;" class="tex" alt="D" />, a <strong>functor</strong> <img src="/extensions/vLaTeX/cache/latex_4ab4a8e1b1343def201689148996e8cd.png" title="F:C\to D" style="vertical-align:-20%;" class="tex" alt="F:C\to D" /> is a map that sends each object <img src="/extensions/vLaTeX/cache/latex_0e29540f708ca8b32bde8e2c33e97582.png" title="x" style="vertical-align:-20%;" class="tex" alt="x" /> in <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> to an object <img src="/extensions/vLaTeX/cache/latex_91281b8b55384164c30dff8ad67a7219.png" title="F(x)" style="vertical-align:-20%;" class="tex" alt="F(x)" /> in <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align:-20%;" class="tex" alt="D" /> and each morphism <img src="/extensions/vLaTeX/cache/latex_fda7a63267491b34b45b8d7b684bb1f8.png" title="f:x\to y" style="vertical-align:-20%;" class="tex" alt="f:x\to y" /> in <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> to a morphism <img src="/extensions/vLaTeX/cache/latex_ddd586710e765e3df32ec4ac5dfb8f2c.png" title="F(f):F(x)\to F(y)" style="vertical-align:-20%;" class="tex" alt="F(f):F(x)\to F(y)" /> in <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align:-20%;" class="tex" alt="D" /> such that:</p> <ol> <li><img src="/extensions/vLaTeX/cache/latex_5ec3dcd4fa96727f6008946ebbeebfa2.png" title="F" style="vertical-align:-20%;" class="tex" alt="F" /> preserves compositions,</li> <li><img src="/extensions/vLaTeX/cache/latex_5ec3dcd4fa96727f6008946ebbeebfa2.png" title="F" style="vertical-align:-20%;" class="tex" alt="F" /> preserves identities. </ol> <p><strong>Definition #2:</strong></p> <p>Given categories <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> and <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align:-20%;" class="tex" alt="D" />, a <strong>functor</strong> <img src="/extensions/vLaTeX/cache/latex_4ab4a8e1b1343def201689148996e8cd.png" title="F:C\to D" style="vertical-align:-20%;" class="tex" alt="F:C\to D" /> is a map that sends each object <img src="/extensions/vLaTeX/cache/latex_0e29540f708ca8b32bde8e2c33e97582.png" title="x" style="vertical-align:-20%;" class="tex" alt="x" /> in <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> to an object <img src="/extensions/vLaTeX/cache/latex_91281b8b55384164c30dff8ad67a7219.png" title="F(x)" style="vertical-align:-20%;" class="tex" alt="F(x)" /> in <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align:-20%;" class="tex" alt="D" /> and each morphism <img src="/extensions/vLaTeX/cache/latex_fda7a63267491b34b45b8d7b684bb1f8.png" title="f:x\to y" style="vertical-align:-20%;" class="tex" alt="f:x\to y" /> in <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> to a morphism <img src="/extensions/vLaTeX/cache/latex_ddd586710e765e3df32ec4ac5dfb8f2c.png" title="F(f):F(x)\to F(y)" style="vertical-align:-20%;" class="tex" alt="F(f):F(x)\to F(y)" /> in <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align:-20%;" class="tex" alt="D" /> such that each commuting diagram in <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> maps to a commuting diagram in <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align:-20%;" class="tex" alt="D" />.</p> <hr /> <p>Mike responded <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7140#Comment_7140">here</a>:</p> <blockquote> <p>@Eric: I would consider your definition #2 to be unbiased, and to include definition #1. The two axioms in definition #1 are both particular sorts of commuting diagrams: a composition of arrows is a commuting triangle, and an identity is a commuting loop.</p> </blockquote> <p>I interpreted Mike's response to mean Definition #1 and Definition #2 were the same, but all Mike really said was #2 includes #1. For them to be the same, #1 would also have to include #2. I'm afraid that might not be the case. I'm afraid #2 might be stronger than #1. I'm not sure, but I think with #2, we WOULD have the image always being a subcategory. What do you think?</p> -
- CommentRowNumber211.
- CommentAuthorMike Shulman
- CommentTimeApr 3rd 2010
They are the same. If
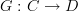 is a functor in the usual sense (i.e. definition #1), and
is a functor in the usual sense (i.e. definition #1), and 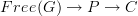 is a commuting diagram factoring through a preorder
is a commuting diagram factoring through a preorder 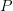 , then since functor composition (in the usual sense) is associative, the induced diagram
, then since functor composition (in the usual sense) is associative, the induced diagram 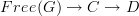 also factors through
also factors through 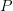 .
.Diagrams in the sense of "diagrams-we-draw-on-a-page" are basically always functors from a free category or equivalently graph maps. I think the point is that there is a different meaning of "diagram" which refers to an arbitrary functor. It is fairly common, for instance, to talk about
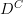 as "the category of diagrams in
as "the category of diagrams in  of shape
of shape  " for arbitrary categories
" for arbitrary categories  and
and  .
.Not every preorder is free on a graph, in fact very few are. For instance, the commuting square is not.
-
- CommentRowNumber212.
- CommentAuthorTodd_Trimble
- CommentTimeApr 3rd 2010
- (edited Apr 3rd 2010)
<div> <p>[Edit: I'm covering much the same ground as Mike just did]</p> <blockquote> A part of me still wishes we could define a diagram as follows ... </blockquote> <p>Again, I personally don't mind our doing that.</p> <blockquote> I like this because diagrams are almost always (I can't think of a counter example) functors from free categories for some graph. </blockquote> <p>A counterexample would be a functor whose domain has just one object and exactly two morphisms. The non-identity morphism could be either idempotent or involutive. This category is not a free category.</p> <p>However, in the context of speaking of commutative diagrams, this sort of thing is arguably a little bit artificial.</p> <blockquote> In fact, that last sentence could probably be improved, because I'm willing to bet that any preorder is a quiver for some graph. </blockquote> <p>Sorry, not true. The commuting square, i.e., the poset consisting of subsets of ${0, 1}$ ordered by inclusion, is not a quiver (free category). Do you see why?</p> <p>(In fact, here's a little factoid I rather enjoy: if the free category on a directed graph has a terminal object, then the graph is a tree.)</p> <blockquote> I interpreted Mike's response to mean Definition #1 and Definition #2 were the same, but all Mike really said was #2 includes #1. For them to be the same, #1 would also have to include #2. I'm afraid that might not be the case. I'm afraid #2 might be stronger than #1. I'm not sure, but I think with #2, we WOULD have the image always being a subcategory. What do you think? </blockquote> <p>The two statements are equivalent. Definition # 1 is the standard definition of functor. It implies definition #2, because functors preserve commuting diagrams.</p> <p>Definition # 2 could be considered an axiom scheme, since you are quantifying over all diagrams in <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align: -20%;" class="tex" alt="C"/>. Probably you see definition #1 more often because there are only two axioms.</p> <p>The image of a category <img src="/extensions/vLaTeX/cache/latex_dc3fcd71eea8cc9d58dab8ea82eae894.png" title="F(C)" style="vertical-align: -20%;" class="tex" alt="F(C)"/> not necessarily being a subcategory has nothing to do with preservation of commuting diagrams. It has to do with the image not necessarily being closed under compositions. I gave an example a while back.</p> </div> -
- CommentRowNumber213.
- CommentAuthorEric
- CommentTimeApr 3rd 2010
- (edited Apr 3rd 2010)
Nice! Thanks Mike.If no one beats me to it, I'll add your suggestions to the nLab.
Edit: And thanks Todd! Yes. Thanks so much. That all makes perfect sense. All my fears are gone :)
-
- CommentRowNumber214.
- CommentAuthornLab edit announcer
- CommentTimeFeb 5th 2019
Added preservation of identity to ideas section. It is misleading to think that a functor does this automatically. Take the terminal category and an idempotent monoid . A functor has the following: but if does not preserve identity then may be the idempotent. I think when these are groupoids, preservation of identity can be dropped but idempotent categories require the restriction.
Anonymous
-
- CommentRowNumber215.
- CommentAuthorMike Shulman
- CommentTimeFeb 5th 2019
-
- CommentRowNumber216.
- CommentAuthorAli Caglayan
- CommentTimeFeb 5th 2019
Also the “categorification” should be of the notion of “identity preserving homomorphisms”?
-
- CommentRowNumber217.
- CommentAuthorMike Shulman
- CommentTimeFeb 5th 2019
A homomorphism (between structures with identities, like monoids or groups) always preserves identities.
-
- CommentRowNumber218.
- CommentAuthorDmitri Pavlov
- CommentTimeNov 21st 2020
-
- CommentRowNumber219.
- CommentAuthorUrs
- CommentTimeJul 12th 2021
-
- CommentRowNumber220.
- CommentAuthornLab edit announcer
- CommentTimeJun 7th 2022
-
- CommentRowNumber221.
- CommentAuthorUrs
- CommentTimeMay 20th 2023
added pointer to:
- Saunders MacLane, §I.3 of: Categories for the Working Mathematician, Graduate Texts in Mathematics 5 Springer (1971, second ed. 1997) [doi:10.1007/978-1-4757-4721-8]