nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorEric
- CommentTimeNov 6th 2009
It's not technically part of the main nLab (yet), but I asked a question at
-
- CommentRowNumber2.
- CommentAuthorEric
- CommentTimeNov 11th 2009
I asked another question at Cograph (ericforgy)
-
- CommentRowNumber3.
- CommentAuthorEric
- CommentTimeNov 12th 2009
*bump*
Any help would be greatly appreciated. Even something like, "Huh?! What on earth are you talking about?" would help focus my question. I'm hoping to understand cographs and category of elements and how they're related (if at all), etc etc. I lost a nights sleep over this as diagrams were racing around my head :) -
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeNov 12th 2009
Right, so the answer to your questionm about higher cographs is basically: Yes.
The cograph of an n-functor is defined almost literally like that of a functor, only that everything is taking palce in the corresponding higher context. So you regard your n-functor
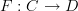 as an n-functor
as an n-functor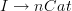
and then look at the weak pullback of the point along this morphism.
But are we ready for this already? I thought we were still waiting to hear back from you about the degree to wich you are happy now with talking about ordinary 1-functors in terms of cographs. So that is clear?
Concerning the other bit of your question:
you may of course consider pulling back along more general maps
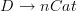 . As D becomes larger, it encodes n ot just a single functor but a whole system of such. And if you want you can call the cooresponding weak pullback of the point the cograph of that system of functors. Just beware that such systems of n-functos are then more traditionally called (n+1)-presheaves on
. As D becomes larger, it encodes n ot just a single functor but a whole system of such. And if you want you can call the cooresponding weak pullback of the point the cograph of that system of functors. Just beware that such systems of n-functos are then more traditionally called (n+1)-presheaves on 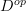 and that the corresponding cograph would be called their n-Grothendieck construction or something like that. But that's just words.
and that the corresponding cograph would be called their n-Grothendieck construction or something like that. But that's just words. -
- CommentRowNumber5.
- CommentAuthorEric
- CommentTimeNov 12th 2009
- (edited Nov 12th 2009)
Thanks!
But you violated your own rule! :)
I've moved your response to Cograph (ericforgy). I'll respond there after I've had some coffee :)
Edit: Fixed the link. Thanks Toby! -
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeNov 12th 2009
<div> <blockquote> But you violated your own rule! :) </blockquote> <p>Yeah, I was thinking about that. But then I thought I didn't really say anything substantive except for agreeing with you.</p> <p>But you are right, I violated my own rule. Not sure what that tells me.</p> <p>No, I am sure. It tells me that I must try harder.</p> </div> -
- CommentRowNumber7.
- CommentAuthorEric
- CommentTimeNov 12th 2009
Yeah, Urs. You are not working hard enough. Get with it! (Please note the sarcasm, I don't know anyone who works harder than you :)) -
- CommentRowNumber8.
- CommentAuthorTobyBartels
- CommentTimeNov 12th 2009
Eric wrote:
I've moved your response to Cograph.
But he meant:
I've moved your response to Cograph (ericforgy).
-
- CommentRowNumber9.
- CommentAuthorEric
- CommentTimeNov 13th 2009
- (edited Nov 13th 2009)
Thanks Urs and Toby!
I'm stuck again :)
I asked whether the
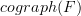 of an
of an  -functor is an
-functor is an 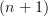 -category.
-category. -
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeNov 13th 2009
No.
Go back to the example that you understand: the cograph of a functor is a category. 1-functor => 1-category.
-
- CommentRowNumber11.
- CommentAuthorEric
- CommentTimeNov 13th 2009
- (edited Nov 13th 2009)
Doh! I was looking at cograph of a 0-functor (i.e. function) is a 1-category...
If you look at the figure on experimental alternative definition of functor, I thought the map
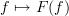 was a 2-morphism. Since the diagram commutes, would that 2-morphism be a 2-identity?
was a 2-morphism. Since the diagram commutes, would that 2-morphism be a 2-identity? -
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeNov 13th 2009
<div> <blockquote> I was looking at cograph of a 0-functor (i.e. function) is a 1-category... </blockquote> <p>Hm, where is that statement taken from?</p> <p><a href="http://ncatlab.org/nlab/show/graph+of+a+function#cograph_of_a_function_11">here</a> at least it does say that for functions it is a set.</p> </div> -
- CommentRowNumber13.
- CommentAuthorEric
- CommentTimeNov 13th 2009
<div> <p>Hmm.. on <a href="https://ncatlab.org/nlab/show/cograph+of+a+functor">cograph of a functor</a> in the section "Cographs of functors between 0-categories" it says:</p> <blockquote> the objects of <img src="/extensions/vLaTeX/cache/latex_a8cdaad55ecdee9f13550a5589288c99.png" title="cograph(f)" style="vertical-align: -20%;" class="tex" alt="cograph(f)"/> are the disjoint union of <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align: -20%;" class="tex" alt="C"/> and <img src="/extensions/vLaTeX/cache/latex_2ee7b824387c9bc0be61af5017684619.png" title="D: Obj(cograph(f))=C\sqcup D" style="vertical-align: -20%;" class="tex" alt="D: Obj(cograph(f))=C\sqcup D"/> and the nontrivial morphisms are of the form <img src="/extensions/vLaTeX/cache/latex_b6b5cb002712bd65456fa20f4b2ea06f.png" title="x\to y" style="vertical-align: -20%;" class="tex" alt="x\to y"/> whenever <img src="/extensions/vLaTeX/cache/latex_718efc8a5e512fc77ccbfd711b617c58.png" title="x\in C" style="vertical-align: -20%;" class="tex" alt="x\in C"/>, <img src="/extensions/vLaTeX/cache/latex_4e769c4f7b075fdff5f6c5ddba332793.png" title="y\in D" style="vertical-align: -20%;" class="tex" alt="y\in D"/> and <img src="/extensions/vLaTeX/cache/latex_72ba6c5cc956519642723a7617ce1e97.png" title="f(x)=y" style="vertical-align: -20%;" class="tex" alt="f(x)=y"/>. </blockquote> <p>That sounds like a 1-category to me (?)</p> </div> -
- CommentRowNumber14.
- CommentAuthorEric
- CommentTimeNov 13th 2009
- (edited Nov 13th 2009)
It seems that Lawvere went one step further and took a quotient by identifying
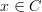 and
and 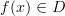 (both considered in
(both considered in 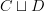 ). In that case, we do get a 0-category. But I don't think we want to consider a cograph to be the result after taking the quotient, but before as in cograph of a functor, in which case the cograph of a 0-functor is a 1-category (I think!)
). In that case, we do get a 0-category. But I don't think we want to consider a cograph to be the result after taking the quotient, but before as in cograph of a functor, in which case the cograph of a 0-functor is a 1-category (I think!) -
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeNov 13th 2009
- (edited Nov 13th 2009)
The cograph of an n-functor is an n-category.
Notice that every n-category is also an m-category for all
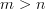 .
.The cograph of a 0-functor=function is a 0-catgeory= set.
The cograph of a 1-functor=functor is a 1-catgeory= category.
And so on.
Lawvere discussed the concept for sets. We have categorified it here.
-
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeNov 13th 2009
Ah, wait, it is a bit more subtle than this makes it sound. Because we are talking about lax ("comma") pullbacks not homotopy pullbacks.
So the cograph of a function regarded as a 0-functor rearded as the pullback of Cat_* is indeed a category. You are right. Its connected components are the Lawvere cograph of the funciton.
Ahm, okay, so I need to give better replies here. But now I have to run. More later.
-
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeNov 13th 2009
Okay, sorry Eric, I sad this at best badly, probaly I said it wrong:
What exactly the cograph of an n-functor is depends on what exactly we are lax-ly (comma-ly) pulling back along
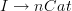 . The different results should all be related by taking connected components of k-morphisms from some degree k on.
. The different results should all be related by taking connected components of k-morphisms from some degree k on.This requires more discussion. I am not sure I have the energy to do justice to this right now. I am inclined to be lazy and just point out that in Lurie's books the case where we pull back functors to (oo,1)-categories is developed in great detail and that nobody has much of an idea for the general (oo,n)-case anyway.
Sorry, not a helpful reply for you. Maybe we can come back to this later.
-
- CommentRowNumber18.
- CommentAuthorEric
- CommentTimeNov 13th 2009
Huh?! :)
Sure. When you quotient out the connected objects everything should agree, but I don't see how the results would be any way related to a (co)graph in any sense of the word I can imagine. You could have an interesting functor with connections going every which way, but if all those are connected, the quotient becomes a single point. How fun is that?! :)
Given 0-categories
 and
and 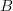 , inclusion maps
, inclusion maps 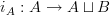 ,
, 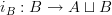 and a 0-functor
and a 0-functor 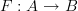 , then we can construct a new category
, then we can construct a new category  with
with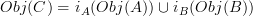
and
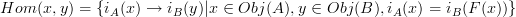
If
 is not
is not 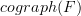 , then what is it?
, then what is it? -
- CommentRowNumber19.
- CommentAuthorTobyBartels
- CommentTimeNov 13th 2009
Ah! The cograph in #13, which I think is the same as what Eric is trying to describe in #18, is a poset, that is a
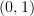 -category, rather than a set, that is a
-category, rather than a set, that is a 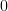 -category or
-category or 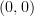 -category. Since Urs is working with a concept from Lurie that makes the cograph of a functor between
-category. Since Urs is working with a concept from Lurie that makes the cograph of a functor between  -categories into an
-categories into an  -category, this makes some sense, even though it doesn\'t match Lawvere's cograph.
-category, this makes some sense, even though it doesn\'t match Lawvere's cograph.But the cograph of a functor between categories, that is
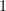 -categories or
-categories or 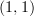 -categories, will still be a
-categories, will still be a 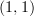 -category. (And the cograph of a functor between
-category. (And the cograph of a functor between 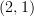 -categories will be a
-categories will be a 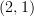 -category, etc; does Lurie's definition even apply to arbitrary functors between arbitrary
-category, etc; does Lurie's definition even apply to arbitrary functors between arbitrary 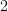 -categories, that is
-categories, that is 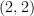 -categories?)
-categories?)The reason that the category defined in #13 is a poset is that, given any two objects, there is always at most one morphism from the one object to the other. I was thinking that this category was also a groupoid, hence equivalent to a set (and the same set as Lawvere's cograph), but that is not true.
-
- CommentRowNumber20.
- CommentAuthorEric
- CommentTimeNov 13th 2009
- (edited Nov 13th 2009)
Ok. So are you saying that the cograph of a functor between
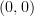 -category is a
-category is a 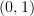 -category, but the cograph of a functor between
-category, but the cograph of a functor between 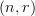 -categories is a
-categories is a 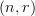 -category otherwise?
-category otherwise?If the thing described in #13 and #18 is not a cograph, what is it?
It seems the concept of what a cograph should be is not clear. Help!!
Let's maybe start by all agreeing on what a cograph should be for a functor between
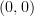 -categories.
-categories. -
- CommentRowNumber21.
- CommentAuthorTobyBartels
- CommentTimeNov 13th 2009
I'm saying that the cograph of a functor between
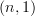 -categories is an
-categories is an 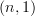 -category. As every
-category. As every 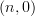 -category may be interpreted as an
-category may be interpreted as an 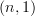 -category, they are included. I don't know what to do with
-category, they are included. I don't know what to do with 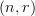 -categories for
-categories for 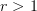 , but perhaps Urs has some ideas. (Lurie considers only functors between
, but perhaps Urs has some ideas. (Lurie considers only functors between  -categories, among which
-categories, among which 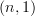 -categories for any
-categories for any  are included. So Lurie does not help with functors between general
are included. So Lurie does not help with functors between general 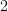 -categories.)
-categories.)Let's maybe start by all agreeing on what a cograph should be for a functor between
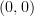 -categories.
-categories.I think that this is the root of the problem. Lawvere defined what this is, in duality with the oridnary notion of the graph of a functor between
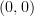 -categories. Then Lurie generalised this to functors between
-categories. Then Lurie generalised this to functors between  -categories, but in such a way that, if you interpret
-categories, but in such a way that, if you interpret 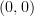 -categories as special
-categories as special  -categories, you get a different result from Lawvere's. (I did not appreciate this fact until this morning.) And that is why we have been confused, I think.
-categories, you get a different result from Lawvere's. (I did not appreciate this fact until this morning.) And that is why we have been confused, I think.I believe that Mike Shulman would teach us to call Lurie's construction the ‘2-cograph’. Presumably the
 -cograph of a functor between
-cograph of a functor between 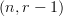 -categories is an
-categories is an 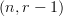 -category, although I don't know whether it is actually possible to define such a thing for
-category, although I don't know whether it is actually possible to define such a thing for 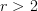 .
. -
- CommentRowNumber22.
- CommentAuthorEric
- CommentTimeNov 13th 2009
- (edited Nov 13th 2009)
Note: I started writing this before seeing Toby's note and then got distracted...
Sticking with sets (thought of as 0-categories)
 and
and 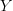 and a 0-functor
and a 0-functor 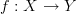 . This situation CAN be thought of as a 1-category with 2 objects and 1-morphism
. This situation CAN be thought of as a 1-category with 2 objects and 1-morphism 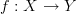 . If we explode this category, the results is what I think the cograph of
. If we explode this category, the results is what I think the cograph of 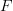 should be. Does that agree with Lawvere's definition?
should be. Does that agree with Lawvere's definition?Now, when we have small 1-categories
 and
and  and a 1-functor
and a 1-functor 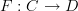 , then I'd think a 2-cograph would be some kind of generalized "category of elements" with 0-morphisms (objects), 1-morphisms between 0-morphisms, and 2-morphisms between 1-morphisms. If not, then "cograph" is not the concept I'm looking for. What would that generalized "exploded 2-category" obtained from a functor be called?
, then I'd think a 2-cograph would be some kind of generalized "category of elements" with 0-morphisms (objects), 1-morphisms between 0-morphisms, and 2-morphisms between 1-morphisms. If not, then "cograph" is not the concept I'm looking for. What would that generalized "exploded 2-category" obtained from a functor be called? -
- CommentRowNumber23.
- CommentAuthorTobyBartels
- CommentTimeNov 13th 2009
Ah, now I see what concrete category you are trying to explode!
I'll think in a minute about how its category of elements relates to the cograph of the function in question. But first I'll address the categorified version.
If we have a functor between
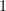 -categories, then this diagram still gives the same diagram as for the functor between
-categories, then this diagram still gives the same diagram as for the functor between 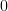 -categories: a category with
-categories: a category with 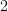 objects and
objects and 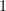 nontrivial morphism. As a concrete category it is different, since the functor to
nontrivial morphism. As a concrete category it is different, since the functor to 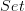 is different, and in fact we really have a functor to
is different, and in fact we really have a functor to 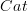 . (So it's a sort of concrete
. (So it's a sort of concrete 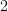 -category that happens to be a
-category that happens to be a 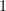 -category.) So even to ask what its explosion is requires that we generalise the category of elements of a concrete category to some sort of concrete
-category.) So even to ask what its explosion is requires that we generalise the category of elements of a concrete category to some sort of concrete 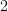 -category (or at least to a category equipped with a functor to
-category (or at least to a category equipped with a functor to 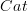 ). I'll think about that too.
). I'll think about that too. -
- CommentRowNumber24.
- CommentAuthorTobyBartels
- CommentTimeNov 13th 2009
First minute's thought: The category of elements of the concrete category given by a functor between
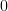 -categories is the cograph in Urs's sense (the one which is a poset), but not the cograph in Lawvere's sense (the one which is a set). I'm starting to think that Lawvere's version is actually not as good as Urs's version. In fact, I think that I should go back and make sure that I got Lawvere's version correct!
-categories is the cograph in Urs's sense (the one which is a poset), but not the cograph in Lawvere's sense (the one which is a set). I'm starting to think that Lawvere's version is actually not as good as Urs's version. In fact, I think that I should go back and make sure that I got Lawvere's version correct! -
- CommentRowNumber25.
- CommentAuthorEric
- CommentTimeNov 13th 2009
Reid Barton gave a very helpful answer at Math Overflow.
He noted that their are two constructions for sets. One resulting in a 0-category and one resulting in a 1-category. He then said that for n-categories for n>0, the results is always an n-category. I still don't quite understand that.
Given morphisms
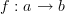 and
and 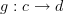 , would you say that a 2-morphism
, would you say that a 2-morphism 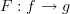 is an identity if there there are morphisms
is an identity if there there are morphisms 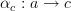 and
and 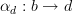 such that
such that 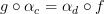 ? If so, then I think I understand why the cograph of a 1-functor is a 1-category. By requiring the diagram at experimental alternative definition of functor to commute, we would be saying all 2-morphisms
? If so, then I think I understand why the cograph of a 1-functor is a 1-category. By requiring the diagram at experimental alternative definition of functor to commute, we would be saying all 2-morphisms 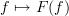 are identity morphisms resulting in a 1-category, not a 2-category.
are identity morphisms resulting in a 1-category, not a 2-category. -
- CommentRowNumber26.
- CommentAuthorTobyBartels
- CommentTimeNov 13th 2009
- (edited Nov 13th 2009)
Second minute's thought: I want to say that the explosion of a
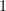 -category equipped with a functor to
-category equipped with a functor to 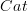 is a double category. When this situation is given by a functor between
is a double category. When this situation is given by a functor between  -categories, this is not the cograph as Urs defines it at cograph of a functor. However, I can kind of see the double category that appears in this situation in picture at experimental alternative definition of functor, so it could well be what you're after.
-categories, this is not the cograph as Urs defines it at cograph of a functor. However, I can kind of see the double category that appears in this situation in picture at experimental alternative definition of functor, so it could well be what you're after. -
- CommentRowNumber27.
- CommentAuthorTobyBartels
- CommentTimeNov 13th 2009
Yes, Reid's answer is interesting; he seems to know about cographs of functors between
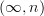 -categories for arbitrarily large
-categories for arbitrarily large  . (But when he says that these are
. (But when he says that these are  -categories, I think that he must mean that these are
-categories, I think that he must mean that these are 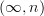 -categories.)
-categories.)I don't know how that works, but if it's correct, then it seems to me that the cograph of a functor between
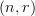 -categories is in general an
-categories is in general an 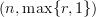 -category. In the case of
-category. In the case of 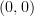 -categories, this gives you a
-categories, this gives you a 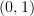 -category, which can be interpreted as a
-category, which can be interpreted as a 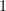 -category but not as a
-category but not as a 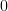 -category, which is why people are saying that it's really a
-category, which is why people are saying that it's really a 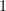 -category. But it's not a
-category. But it's not a 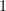 -category in full glory, but merely a
-category in full glory, but merely a 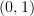 -category.
-category.However, perhaps the thing that you are after is some sort of
 -tuple category, as I hinted in my last answer. I don't know how that would work, either, but maybe we can figure it out.
-tuple category, as I hinted in my last answer. I don't know how that would work, either, but maybe we can figure it out. -
- CommentRowNumber28.
- CommentAuthorUrs
- CommentTimeNov 13th 2009
- (edited Nov 13th 2009)
Yes, Toby, exactly, there is a (0,1)- and then an (n,n+1) aspect here which I hadn't fully appreciated in my first quick responses to Eric. Sorry for causing confusion.
Right now I don't quite feel I can find the energy to do this topic justice, and I am glad to see that you and Eric are putting so much thought into this now. I'll try to come back to this a little later. Gotta rush now.
-
- CommentRowNumber29.
- CommentAuthorTobyBartels
- CommentTimeNov 13th 2009
But is there an
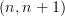 -aspect in general? Is the cograph of a functor between
-aspect in general? Is the cograph of a functor between 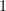 -categories a
-categories a 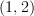 -category (a
-category (a 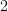 -poset)? If so, I don't see it.
-poset)? If so, I don't see it. -
- CommentRowNumber30.
- CommentAuthorEric
- CommentTimeNov 14th 2009
- (edited Nov 14th 2009)
Let's try to work through it. Do we agree that a cograph of a 0-functor between
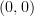 -categories is a poset? (which I guess is a
-categories is a poset? (which I guess is a 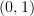 -category)
-category)Also, do we agree that this cograph is the category of elements for the 1-category
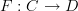 ?
? -
- CommentRowNumber31.
- CommentAuthorTobyBartels
- CommentTimeNov 14th 2009
Yes, I agree with that. At least, that is the cograph as defined at cograph of a functor; Lawvere's cograph is different.
-
- CommentRowNumber32.
- CommentAuthorEric
- CommentTimeNov 14th 2009
- (edited Nov 14th 2009)
<div> <p>I like the comment at <a href="https://ncatlab.org/nlab/show/graph+of+a+function">graph of a function</a> in the section "Cograph of a function" where it says</p> <blockquote> The cograph of <img src="/extensions/vLaTeX/cache/latex_43c09e88e076b2d340501a0744aa1639.png" title="f" style="vertical-align: -20%;" class="tex" alt="f"/> in the sense of Lawvere is the set of connected components of this category, i.e. <img src="/extensions/vLaTeX/cache/latex_96a2d321cc4bbac79ec605e84f714214.png" title="\i_0(cograph(f))" style="vertical-align: -20%;" class="tex" alt="\i_0(cograph(f))"/>. </blockquote> <p>So I suggest we use the definition at <a href="https://ncatlab.org/nlab/show/cograph+of+a+functor">cograph of a functor</a> and note that Lawvere's "cograph" is <img src="/extensions/vLaTeX/cache/latex_f1a7042d12b75231e845cda99141efa1.png" title="\pi_0" style="vertical-align: -20%;" class="tex" alt="\pi_0"/> of this. Sound ok?</p> <p>If so, maybe we can try to spell out what a cograph of a 1-functor between categories would be using Lurie's paper as a guide.</p> <p>How about Attempt #3 at <a href="https://ncatlab.org/ericforgy/show/Cograph">Cograph (ericforgy)</a>?</p> </div> -
- CommentRowNumber33.
- CommentAuthorTobyBartels
- CommentTimeNov 14th 2009
- (edited Nov 14th 2009)
So I suggest we use the definition at cograph of a functor and note that Lawvere's "cograph" is
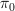 of this. Sound ok?
of this. Sound ok?I'm still not too sure about this. I mean, Lawvere said ‘cograph’ first, and it's a very natural idea: where the graph is a subset of the product, the cograph is a quotient set of the coproduct. It doesn't seem right to say that Lawvere got it wrong.
The problem is that ‘quotient’ changes its meaning when you extend the context from sets to categories to
 -categories (while ‘sub-’, ‘product’ and ‘coproduct’ do not). So there is an argument to be made that Lawvere got it wrong, by working in too restricted a context; I'm just not certain yet.
-categories (while ‘sub-’, ‘product’ and ‘coproduct’ do not). So there is an argument to be made that Lawvere got it wrong, by working in too restricted a context; I'm just not certain yet.Anyway, I'll respond at Cograph (ericforgy).
-
- CommentRowNumber34.
- CommentAuthorEric
- CommentTimeNov 14th 2009
- (edited Nov 14th 2009)
If you reverse the arrows of a diagram representing a "graph of a function", do you get a "quotient set of the coproduct"? If so, then "cograph" should be "quotient set of the coproduct".
In other words, are "subset" and "quotient" kind of like "dual" concepts?
-
- CommentRowNumber35.
- CommentAuthorTobyBartels
- CommentTimeNov 14th 2009
Yes, subobjects and quotient objects are indeed dual. Although I'm not sure that you're reversing the right arrows; reverse the arrows (which lie in
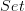 , not in the graph itself) in an arrow-theoretic definition of graph of a function to get an arrow-theoretic definition of Lawvere's cograph of a function.
, not in the graph itself) in an arrow-theoretic definition of graph of a function to get an arrow-theoretic definition of Lawvere's cograph of a function.Now take that diagram and interpret it as lying in
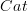 (although the starting data happen to be still two sets and a function between them, that is two discrete categories and a functor between them). Then the original diagram (defining the graph) will define the same thing as before (a discrete category which is the same as the set defined before), but the diagram defining the cograph will define Urs's cograph (which is not a discrete category), differently from before.
(although the starting data happen to be still two sets and a function between them, that is two discrete categories and a functor between them). Then the original diagram (defining the graph) will define the same thing as before (a discrete category which is the same as the set defined before), but the diagram defining the cograph will define Urs's cograph (which is not a discrete category), differently from before. -
- CommentRowNumber36.
- CommentAuthorTobyBartels
- CommentTimeNov 14th 2009
Regard Tom Leinster's answer to you on MathOverflow:
You should go and look at that picture if he tells you. If you do, I think that you'll find further evidence that —even though Lawvere himself defined it to be a set— it really is better to make the cograph of a function be a poset. I'm now inclined to go ahead and just say so at cograph (ending my hesitation in #33).
-
- CommentRowNumber37.
- CommentAuthorEric
- CommentTimeNov 14th 2009
I can kind of understand Tom's notation for graph:
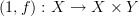 because I presume
because I presume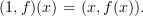
But then the graph is not a subset of
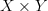 , but its image is a subset.
, but its image is a subset.I'm less clear on what
![[f,1]^T: X+Y\to Y [f,1]^T: X+Y\to Y](/extensions/vLaTeX/cache/latex_a5daef7044f420bad2dbb11b6938c8b2.png) means. How does it act on elements of
means. How does it act on elements of 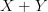 ?
? -
- CommentRowNumber38.
- CommentAuthorTobyBartels
- CommentTimeNov 15th 2009
But then the graph is not a subset of
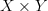 , but its image is a subset.
, but its image is a subset.Sure it's a subset; see subset. To a category theorist, there is no essential difference between an injective function and its image, as a subset of the target.
I like to write
![[f,1]^T [f,1]^T](/extensions/vLaTeX/cache/latex_51058b9b731e59041cca4381e4bae63a.png) as
as 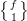 when I can, because the definition is this:
when I can, because the definition is this: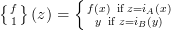
See copairing.
-
- CommentRowNumber39.
- CommentAuthorEric
- CommentTimeNov 15th 2009
Thanks. But how can you deduce that from the diagram? I'm having trouble, in general, converting diagrams to equations (which is maybe misguided anyway). In particular, I'm having trouble parsing the diagrams at graph of a functor, cograph of a functor, and graph of a function.
-
- CommentRowNumber40.
- CommentAuthorTobyBartels
- CommentTimeNov 15th 2009
But how can you deduce that from the diagram?
I can't tell which diagram you mean. I'm explaining Tom's notation; there's no diagram on those pages that tries to do this, while copairing gives it explicitly.
-
- CommentRowNumber41.
- CommentAuthorEric
- CommentTimeNov 15th 2009
Things are so hectic, I don't even remember what I was talking about. Our one-way flight to HK leaves on Wednesday! :)
I saw somewhere recently a diagram for graph and it said a cograph was the same diagram with arrows reversed. Then Tom's answer involved pairings and copairings and maybe I was thinking there should be some nice diagram illustrating the relation. Basically, now I understand the notation, but the notation should come from some diagram. I'd like to understand that diagram.
More importantly, though, I'd like to understand the diagrams on the nLab pages I referenced.
-
- CommentRowNumber42.
- CommentAuthorEric
- CommentTimeNov 16th 2009
- (edited Nov 16th 2009)
I added some diagrams to Cograph that I hope to one day include on cograph of a functor (once I understand things better).
-
- CommentRowNumber43.
- CommentAuthorTobyBartels
- CommentTimeNov 17th 2009
Good luck in Hong Kong!
-
- CommentRowNumber44.
- CommentAuthorEric
- CommentTimeNov 17th 2009
<div> <blockquote> Good luck in Hong Kong! </blockquote> <p>Thanks! I'll be happy to GET to Hong Kong :)</p> <p>Ok! My diagrams at <a href="https://ncatlab.org/ericforgy/show/Cograph">Cograph (ericforgy)</a> are correct now. However, I don't yet see how they relate to the diagrams on the nLab, e.g. <a href="https://ncatlab.org/nlab/show/cograph+of+a+functor">cograph of a functor</a>.</p> <p>Whenever I see "co"-something, I usually try to think of a diagram describing "something" and then the "co"-something is the same diagram with arrows reversed. That doesn't seem to be the case with "graph" and "cograph" or am I looking at the wrong diagrams?</p> </div> -
- CommentRowNumber45.
- CommentAuthorEric
- CommentTimeNov 17th 2009
The diagrams at Cograph (ericforgy) are based on Tom's answer on Math Overflow, but I am still having trouble relating them to what is on the nLab, e.g. cograph of a functor.
1 to 45 of 45