nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeNov 11th 2009
created stub for E-k-operad
-
- CommentRowNumber2.
- CommentAuthorTobyBartels
- CommentTimeNov 11th 2009
I think that the name should be E-k operad (which you already made a redirect); more generally, it should be ‘
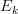 operad’, not ‘
operad’, not ‘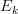 -operad’. Compare: an ‘
-operad’. Compare: an ‘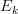 -ring’ is like a monoid but different, because it's been hit with this
-ring’ is like a monoid but different, because it's been hit with this 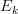 thing. But that's not what we have here; the
thing. But that's not what we have here; the 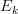 operad is an operad, and it hasn't been hit with any
operad is an operad, and it hasn't been hit with any 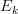 thing; it is the
thing; it is the 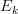 thing.
thing.Am I right?
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeNov 11th 2009
I see, good point. I haven't thought much about this. But, right, it's the operad named
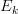 , of course.
, of course.Have changed the page name now.
-
- CommentRowNumber4.
- CommentAuthorTobyBartels
- CommentTimeNov 11th 2009
Should E-infinity operad redirect there too, or does it get its own page?
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeNov 11th 2009
Eventually it should probably have its own page. Maybe at the moment it would be more convenient to have a redirect.
Also the E-1 operad aka Ass should eventually get its own page. And maybe E-2 and E-3. And E-oo. n and one-two-three-infinity. As with n-categories.
-
- CommentRowNumber6.
- CommentAuthorTobyBartels
- CommentTimeNov 11th 2009
n and one-two-three-infinity. As with n-categories.
Now you know my next question:
Is there an
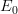 operad?
operad? -
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeNov 11th 2009
I suppose that's the trivial operad. The terminal operad.
Now I foretell your next question...
-
- CommentRowNumber8.
- CommentAuthorEric
- CommentTimeNov 11th 2009
:D -
- CommentRowNumber9.
- CommentAuthorMike Shulman
- CommentTimeNov 11th 2009
I don't think it's really accurate to talk about the
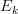 operad. I always thought that one talked about an
operad. I always thought that one talked about an 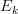 operad, of which the little k-cubes operad is just the most common example. For instance, there is the little k-disks operad. And in the cases k=1 and
operad, of which the little k-cubes operad is just the most common example. For instance, there is the little k-disks operad. And in the cases k=1 and  there are lots more
there are lots more 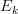 operads; for instance, the linear isometries operad is
operads; for instance, the linear isometries operad is 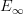 .
. -
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeNov 11th 2009
- (edited Nov 11th 2009)
Right, i thought about that but then was being lazy. I need to polish the terminology. I might have been, as you may have noticed, under the influence of Lurie's latest. He writes
![\mathbb{E}[k] \mathbb{E}[k]](/extensions/vLaTeX/cache/latex_6a45e62b997d1cd601b9769c855044d7.png) specifically for the little cubes thingy.
specifically for the little cubes thingy.I am not sure, what should be the pattern here? Is the blackboard-boldface to be read as indicating that little cubes are meant?
-
- CommentRowNumber11.
- CommentAuthorMike Shulman
- CommentTimeNov 12th 2009
Far be it from me to claim to understand Lurie's notation and terminology. Peter May writes
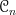 for the little n-cubes operad (
for the little n-cubes operad (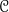 for "cubes"?).
for "cubes"?).
1 to 11 of 11