nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeNov 19th 2009
added illustrating diagram to transfinite composition
I also renamed the resulting composite morphism into
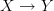 . Hope I did this consistently.
. Hope I did this consistently. -
- CommentRowNumber2.
- CommentAuthorTodd_Trimble
- CommentTimeNov 19th 2009
Another instance of transfinite composition was related to me by Jim Stasheff; it's in Milnor's proof that fiber bundles have the homotopy lifting property. At some point I'll see if I can record it in the Lab. -
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeNov 19th 2009
<div> <blockquote> Another instance of transfinite composition was related to me by Jim Stasheff; it's in Milnor's proof that fiber bundles have the homotopy lifting property. At some point I'll see if I can record it in the Lab. </blockquote> <p>That would great. I am not actually aware of how that proof works.</p> </div> -
- CommentRowNumber4.
- CommentAuthorTodd_Trimble
- CommentTimeNov 19th 2009
Actually, it may be (probably is) different from the transfinite composition described on that page. I'll have to jog my memory a bit. -
- CommentRowNumber5.
- CommentAuthorTodd_Trimble
- CommentTimeNov 20th 2009
I will now try to jot down some scattered memories of the conversation with Stasheff from ages ago at Milnor slide trick.
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeApr 5th 2016
- (edited Apr 5th 2016)
I have tried to make the entry transfinite composition more readable:
I included a quick self-contained definition of ordinals and limit ordinals (for the case with LEM). For if any reader really needs to be reminded, then presently clicking on ordinal sends him or her off onto a long, long chase, until the definition is fully assembled. (Eventually all these entries on XY-orders could be streamlined for public consumption, but I won’t do this right now.)
I changed the name of the transfinite composition diagram from to . That allowed to remove various clauses on how notation is to be matched and simply have the transfinite composite be labeled .
I reordered the two pieces of the definition. Now it first states what the diagram is, then it says how the transfinite composite itself is the given by the colimit. (Previously it was a highly nested sentence starting with “is the colimit” and only then beginning to say of which diagram subject to which conditions).
-
- CommentRowNumber7.
- CommentAuthorManuel Araújo
- CommentTimeMar 9th 2024
- (edited Mar 9th 2024)
Hi!
There is something which seems confusing to me: at the start of Definition 2.3 I was assuming the way one regards an ordinal as a category is by having the set of objects be the underlying set and letting the order relation determine the morphisms. But then it seems a diagram indexed by also assigns values to limit ordinals < , which are not elements in the underlying set.
So it seems objects of as a category are ordinals < and the morphisms are determined by the order on ordinals <. Is that correct?
EDIT: Sorry, I think I understand why these two things are the same, but I don’t know how to delete my comment.
-
- CommentRowNumber8.
- CommentAuthorHurkyl
- CommentTimeMar 9th 2024
- (edited Mar 9th 2024)
It sounds like you are correct, with one correction. In ZFC, one typically defines ordinals so that you actually have an equality
So, the limit ordinals that satisfy are, in fact, members of the set .
If you’re not using this construction, it is still common to use this same language, and implicitly adapt it to your situation. E.g. what you consider the “underlying set” should indeed have elements that correspond to all ordinals less than , including the limit ordinals.
-
- CommentRowNumber9.
- CommentAuthorManuel Araújo
- CommentTimeMar 9th 2024
Thanks! And I guess one can get an isomorphism between and {| is an ordinal satisfying < } by mapping to the ordinal {y: y<x}, with inverse mapping to {y: y>x for all }.
1 to 9 of 9