Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory internal-categories k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: motivic cohomology

Bottom of Page

1 to 24 of 24

  1.  
    • CommentRowNumber1.
    • CommentAuthorUrs
    • CommentTimeNov 19th 2009

    created a stub for motivic cohomology in reply to a question here

    Zoran (or anyone), can you say something about how that related to motives?

    • CommentRowNumber2.
    • CommentAuthorUrs
    • CommentTimeNov 19th 2009

    I daringly added to motive an "Idea" section and a rough idea of the Definition.

    still don't know what the relation to motivic cohomology is, though...

    • CommentRowNumber3.
    • CommentAuthorUrs
    • CommentTimeNov 19th 2009
    • (edited Nov 19th 2009)

    These lecture notes by Voevodsky et al. are useful. They would be even more useful if the authors stopped just for a second to tell the reader what the heck it actually is they are heading for, but okay.

    Prop 14.16 tells us how motivic cohomology knows about certain hom-sets in the category of motives.

    I have included a brief remark at As hom-sets of motives.

    • CommentRowNumber4.
    • CommentAuthorzskoda
    • CommentTimeNov 19th 2009
    • (edited Nov 19th 2009)
    The way the entry is made is pretty orthogonal to my picture of the subject so I can not sensibly contribute without trying to understand your statements there first. First of all, one should distiguish just sheaves from sheaves with transfers, the distinction should not be ommited. The idea section for motives is about a tactics of realization of motives, not about motives themselves. The true idea is that various kinds of cohomologies in nice examples like elliptic curves have similarities like the same dimensions, hence one conjectures existence of a universal theory -- that should be motivic cohomology, and it should reflect the images of varieties in a way that their images "motives" organize into an abelian category. Motivic complexes are something from the vision of Beilinson. Motives are not realized yet, Voevodsky has just an approximation, a corresponding should-be-derived-category of motives.
    • CommentRowNumber5.
    • CommentAuthorUrs
    • CommentTimeNov 20th 2009
    • (edited Nov 20th 2009)

    Okay, I don't really know about this and don't mean to be proposing any specific picture. I just tried to summarize what I saw in these notes. I liked them, because this was the first time that I actually saw an explicit definition of what a motive is. But I understand when you say that this definition is not necessarily what other people are looking for.

    • CommentRowNumber6.
    • CommentAuthorTobyBartels
    • CommentTimeNov 20th 2009

    Zoran, I would like to see what you would write for an Idea section at motive. If Urs's article is too orthogonal, go the bottom, add *** to make a horizontal rule, and then put your article underneath. We can fit them together afterwards.

    • CommentRowNumber7.
    • CommentAuthorUrs
    • CommentTimeNov 20th 2009

    Zoran, what you put at Voevodsky motive, does that refer to the definition in Mazza-Voevodsky-Weibel that I quote at motive? Or is that yet another definition?

    • CommentRowNumber8.
    • CommentAuthorzskoda
    • CommentTimeNov 20th 2009
    You see the idea of correspondences is from the very begining in ALL known direct approaches to motives (though motivic homotopy theory does not need necessarily, but this is indirect approach), they are in the early Manin-s paper pver 40 years ago, they are used in the construction of pure motives and so on. But WHICH correspondences this is not trivial fact, it is not as mechanic as general nonsense mantras like "groupoidification". Namely if the geometric correspondences are not defined CAREFULLY one does not have well defined composition, that is the place where the finiteness conditions are important. While one has a nonderived version of pure motives, wider category of MIXED motives is not realized but only its derived category which has more than one way to be constructed. Among crucial ideas of Voevodsky is to use sheaves with TRANSFER, then it is important that he found the correct category of "finite correspondences" (which do compose and have some other good features) and the usage of correct Grothendieck topologies, plus usage of analogies with singular homology in topology which nobody dared to utilize/realize in this setup before (he had such ideas already in late 1980s).
    • CommentRowNumber9.
    • CommentAuthorUrs
    • CommentTimeNov 20th 2009
    This comment is invalid XHTML+MathML+SVG; displaying source. <div> <blockquote> it is important that he found the correct category of "finite correspondences" </blockquote> <p>And that's the one the entry points to, or isn't it?</p> <p>I am not sure what you want to have changed. Should we add a sentence saying "This is one proposed definition, other people are thinking about other definitions." ?</p> </div>
    • CommentRowNumber10.
    • CommentAuthorUrs
    • CommentTimeNov 20th 2009

    How do "pure motives" relate to the definition in the Voevodsky-Weibel lectures?

    Do you think these lectures give a wrong impression of the subject?

    • CommentRowNumber11.
    • CommentAuthorUrs
    • CommentTimeNov 20th 2009
    • (edited Nov 20th 2009)

    I have now added a section Motivic cohomology -- Idea where I try to say clearly that there was first Grothendieck's hypothetical ideas and then later Voevodsky's proposal for a concrete realization.

    I renamed the "Definition"-section into "Voevodsky's definition", similarly at motive itself (to which i haven't yet added a similar expanded "Idea" section).

    • CommentRowNumber12.
    • CommentAuthorzskoda
    • CommentTimeNov 20th 2009
    • (edited Nov 20th 2009)
    No, I am saying that a concrete REALIZATION is not the IDEA of motives. The IDEA is that various cohomologies give almost the same answer for good varieties and this DEEP fact points toward existence of UNIVERSAL cohomology theory, and its universal setup for it, an ABELIAN category of motives. I do not understand at all the statement of "abelian cohomology" with the "coefficients in motivic complexes" quite, the way it is written. You possibly meant something similar or I do not understand the thing.

    I REPEAT again that Voevodsky did NOT realize motives but just their derived version, forming the derived category of mixed motives. For usual PURE motives (not mixed) one has the true version (nonderived), the procedure in several steps is explained at pure motive and it involves a DIFFERENT kind of correspondences, known much before. And again one should be careful at which place to use sheaves with transfer and where usual sheaves. I added few clarifications at motive but I am not comfortable to contribute to a so difficult entry without thinking and reading (I did not study this subject for many months). There are so many formalisms and constructions in this area and if one gets specific, one should be careful in which setup it is used, so using simultaneously different references could lead to contradictions if it is not very carefully done. The business of pure motives is much simpler and more classical and approached more or less in a standardized way, that is why I done a short sketch at pure motive at some point. Look at the arxiv survey of Mahanta for a good elementary general introduction of that part of the story.

    Though some constructions are done for more general schemes, the motives are in fact about varieties (just a small nice subcategory), and it is as a rule over a field.
    • CommentRowNumber13.
    • CommentAuthorUrs
    • CommentTimeNov 20th 2009
    This comment is invalid XHTML+MathML+SVG; displaying source. <div> <blockquote> I do not understand at all the statement of "abelian cohomology" with the "coefficients in motivic complexes" </blockquote> <p>I really did nothing but open the Voevodsky lectures and copied the statements from there. He defines a complex of sheaves called the motivic complex and defines motivic cohomology to be sheaf cohomology with coefficients in that.</p> <blockquote> I added few clarifications at motive </blockquote> <p>Thanks.</p> </div>
    • CommentRowNumber14.
    • CommentAuthorzskoda
    • CommentTimeNov 20th 2009
    • (edited Nov 20th 2009)
    After ONE HOUR of working on a response the outage of password (the automatic timing logout) destroyed all my material when sending it here. I hate automatic changes. In fact I was supposedly still logged on but it was asking me to do some humanity check which I failed twice (some letters look unrecognizable, in general the handwriting on human checks on internet is based towarfd habits in american handwriting and puts us others at disadvantage; I even lost a money card in US for similar reasons and had to pay fees for reissuing it).

    I will write now below shorter version below from memory.
    • CommentRowNumber15.
    • CommentAuthorzskoda
    • CommentTimeNov 20th 2009
    • (edited Nov 21st 2009)
    > I really did nothing but open the Voevodsky lectures and copied the statements from there.

    But in original Idea section of motivic complex statement was

    "abelian sheaf cohomology of sheaves on the Zariski or etale site of X ... with coefficients in a complex of sheaves A called the motivic complex."

    or shorter "cohomology of sheaves with coefficient in a complex of sheaves" ??

    I do not understand this: cohomology of which sheaves with coeficients in other (complex of) sheaves? It is I guess just the usual (abelian) HYPERcohomology of the motivic complex of sheaves with transfers on X, which makes sense a priori for smooth X over a field (not all schemes, otherwise you get unbounded complexes and no finiteness conditions to define the hypercohomology). I do not know how much results for other bases (say for families) are possible, or even meaningful.

    On the other hand I am happier with the current version.

    I should point out that Voevodsky himself added to the confusion as he in his early achievements in early 1990s claimed that Grothendieck made a mistake by expecting that motives would make an abelian category. Like don't you see, nobody has it, this viewpoint failed and I constructed in fact a triangulated category of motives. Not derived motives, motives.

    So it stayed to say motive for what should have been consistently called derived motive. Though for the very category D(MM) people often are more careful saying either category of Voevodsky motives or derived category of mixed motives.
    • CommentRowNumber16.
    • CommentAuthorUrs
    • CommentTimeJan 26th 2010
    • (edited Jan 26th 2010)

    in the previous version of motivic cohomology I said that one forms the stabilization of 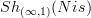Sh_{(\infty,1)}(Nis). That's not quite precise: the point is -- as explained in the references linked to there -- that one stabilizes not with respect to the "categorical" or "simplicial" sphere, but with respect to the "geometric" sphere, the Tate sphere 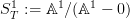S^1_T := \mathbb{A}^1/(\mathbb{A}^1-{0}). I have added remarks about this now, but just ever so briefly. Needs to be expanded on later.

    This happens to be closely related to the discussion we are having over G-equivariant stable homotopy theory, elsewhere. There, too, it seems the point is that the spectra are defined not with respect to the categorical/simplicial spheres, but with respect to the "geometric" spheres.

    I am being told that for the G-equivariant case a very insightful discussion of this aspect is in two article Andrew Blumberg. Probably the first two ones listed here. I am going to look at these now.

    • CommentRowNumber17.
    • CommentAuthorTobyBartels
    • CommentTimeJan 26th 2010

    @ Urs #16

    Probably the first two ones listed here.

    There's no link there.

    • CommentRowNumber18.
    • CommentAuthorUrs
    • CommentTimeJan 26th 2010
    • (edited Jan 26th 2010)

    Thanks. Misplaced quotation mark: here

    But I have added the reference to the entry, meanwhile.

    • CommentRowNumber19.
    • CommentAuthorUrs
    • CommentTimeJan 28th 2010

    added a section grading and bigrading to motivic cohomology where I try to say precisely what the Tate sphere is and precisely what the bigrading is.

    I think I know what i am doing (following the cited references) but some expert should eventually check that I got the conventions right and everything.

    Concerning my query box at cohomology in the section on bigrading, where I propose that one should look at 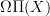\Omega \Pi(X) as that gives something that is generated from categorical and geometric speheres:

    maybe that's precisely what captures the passage to the Tate sphere 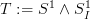T := S^1 \wedge S^1_I , i.e. the smasch product of both spheres. Both spheres at once.

    • CommentRowNumber20.
    • CommentAuthorUrs
    • CommentTimeFeb 25th 2010
    • (edited Feb 25th 2010)

    Peter Arndt made two useful comments at motivic cohomology. One of them I reworked a bit to fit into the text. See the history for details.

    • CommentRowNumber21.
    • CommentAuthorzskoda
    • CommentTimeFeb 25th 2010

    Is Peter also in nforum or only in nlab ? Say hello to this enthusiastic young fellow :)

    • CommentRowNumber22.
    • CommentAuthorUrs
    • CommentTimeFeb 25th 2010

    Peter Arndt further added a few paragraphs to the beginning of the section on Chow groups

  23. Fixed dead link to Hoyois’ paper “From algebraic cobordism to motivic cohomology”

    Thomas Brazelton

    diff, v48, current

    • CommentRowNumber24.
    • CommentAuthorAnton Hilado
    • CommentTimeAug 5th 2023

    Added applications section and example application to the construction of Euler systems.

    diff, v49, current

1 to 24 of 24

  1.