nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorTodd_Trimble
- CommentTimeNov 20th 2009
Somewhat stubby beginning, but with a link to an old paper of Barr which may turn out to be useful for universal algebra in a monoidal category. Some discussion of measuring coalgebras is generalized to the framework of PROPs.
-
- CommentRowNumber2.
- CommentAuthorTobyBartels
- CommentTimeNov 21st 2009
I moved this to CocommCoalg to fit other category titles, and added it to category:category.
-
- CommentRowNumber3.
- CommentAuthorzskoda
- CommentTimeNov 21st 2009
- (edited Nov 21st 2009)
I find the notation for the category two long $cCoalg$ or $commCoalg$ is good enough. While it is important to distinguish associativity and coassociativity for bialgebras, for coalgebras saying coassociativity of associativity, commutativity or cocommutativity really does not matter. Like saying associative comultiplication is good enough (and seen and heard in community, though more rarely than the "correct versions".
More interesting is this catch. In category theory there are representable functors and corepresentable functors. Of course representable are contravariant and corepresentable are covariant. But in modern language one does not say any more contravariant functor $A\to B$ but a says just functor from $A^{op}\to B$. In this modern A representable functor $C\to B$ is the same as a corepresentable functor $(C^{op})^{op}\to B$, but the latter is simply $C\to B$. So corepresentable functor $C\to B$ is the same as representable functor $C\to B$, unless we know distinguish $(C^{op})^{op}$ and $C$. But then what would be the definition that contravariant is the same as covariant from the opposite... We have two choices: either never use word contravariant and always use op when you mean op and always use the same word representable, or another old choice be careful when you mean covariant functor from Cop or contravariant from C, and then also distinguish representable (as we now KNOW we talk about contravariant and not covariant from op) and corepresentable (as we now know we talk covariant).
-
- CommentRowNumber4.
- CommentAuthorMike Shulman
- CommentTimeNov 21st 2009
I generally say "representable" in both the covariant and contravariant case.
-
- CommentRowNumber5.
- CommentAuthorzskoda
- CommentTimeNov 21st 2009
Modern and consistent guy :)
-
- CommentRowNumber6.
- CommentAuthorTodd_Trimble
- CommentTimeNov 21st 2009
So do I, Zoran, and I would like to know who says "corepresentable". To me it would be like saying "co-universal": a word no one (that I know) uses.
-
- CommentRowNumber7.
- CommentAuthorzskoda
- CommentTimeNov 21st 2009
Wow I am messing with wrong people then...
-
- CommentRowNumber8.
- CommentAuthorTobyBartels
- CommentTimeNov 21st 2009
Zoran (or Todd, if you like his suggestions), move to CommCoalg (or whatever) if you like, it won't bother me.
And for the record, I also never say ‘corepresentable’; it sounds a bit odd to me, although I can see the point of it now.
-
- CommentRowNumber9.
- CommentAuthorTodd_Trimble
- CommentTimeNov 21st 2009
- (edited Nov 21st 2009)
I can also see the point of dropping the 'co' as in Zoran's first suggestion; I personally find it tiresome to have to put 'co' in front of everything in coalgebraland (cofree cocommutative counital coalgebra, etc.).
While we're on the topic: I don't like naming it co-yoneda lemma. To me, that is the Yoneda lemma, or at least one of its equivalent forms. I would sooner identify the co-yoneda lemma as having something to do with what I would call the co-yoneda embedding,
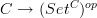 , saying something along the lines of "every copresheaf is canonically a limit of functors of the form
, saying something along the lines of "every copresheaf is canonically a limit of functors of the form 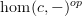 ." Maybe I should have spoken about this sooner.
." Maybe I should have spoken about this sooner. -
- CommentRowNumber10.
- CommentAuthorMike Shulman
- CommentTimeNov 22nd 2009
To me the Yoneda lemma says that natural transformations from a representable functor hom(c,-) into a presheaf F are in natural bijection with F(c). I really don't see how that says the same thing as that every presheaf is canonically a colimit of representables. I suppose one could argue that they're equivalent, in the same way that everything in category theory is equivalent to everything else. But I think "every co-presheaf is canonically a limit of representable" is much more equivalent to "every presheaf is a colimit of representables," since they only differ by a single "op."
-
- CommentRowNumber11.
- CommentAuthorTodd_Trimble
- CommentTimeNov 22nd 2009
- (edited Nov 22nd 2009)
I see either statement as more sharply given by the statement that bimodules
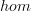 are unit bimodules. This gives that for
are unit bimodules. This gives that for 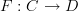 , we have
, we have 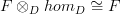 , which is the colimit of representables statement (particularly for a bimodule
, which is the colimit of representables statement (particularly for a bimodule 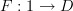 which is a presheaf), or
which is a presheaf), or 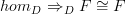 (where
(where 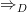 is adjoint on one side to tensor product), which gives the classical Yoneda lemma. The statement I alluded to for what I would call "co-yoneda lemma" is then the formal
is adjoint on one side to tensor product), which gives the classical Yoneda lemma. The statement I alluded to for what I would call "co-yoneda lemma" is then the formal 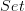 -enriched dual.
-enriched dual.Naturally, all dual statements are just an "op" away!
-
- CommentRowNumber12.
- CommentAuthorMike Shulman
- CommentTimeNov 22nd 2009
Yes, I agree 100%, both statements follow from hom being a unit bimodule. But I think there is more of a difference between saying that
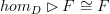 and saying that
and saying that 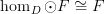 , than between the first one interpreted in
, than between the first one interpreted in 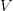 -Mod versus in
-Mod versus in 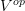 -mod.
-mod.Can you give some reason why you think that these two statements "are" two equivalent forms of the Yoneda lemma, whereas the other dual version is "more different" and merits the "co-"?
-
- CommentRowNumber13.
- CommentAuthorTodd_Trimble
- CommentTimeNov 23rd 2009
- (edited Nov 23rd 2009)
As you know, "co" is the prefix generally used for formally dual concepts. So on those grounds, "co-yoneda embedding of
 " should refer to
" should refer to 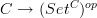 , and "co-yoneda lemma" would then refer to dual properties ascribed to this embedding. That's all I meant . Questions of "more difference" would not be particularly relevant. (I mean, I'd be happy just calling it "yoneda lemma" for either the classical statement or its dual -- just forget "co-yoneda" altogether! I don't even like the term from the get-go. But if I had to name anything the "co-yoneda lemma", then to avoid confusion it would be the formally dual statement.)
, and "co-yoneda lemma" would then refer to dual properties ascribed to this embedding. That's all I meant . Questions of "more difference" would not be particularly relevant. (I mean, I'd be happy just calling it "yoneda lemma" for either the classical statement or its dual -- just forget "co-yoneda" altogether! I don't even like the term from the get-go. But if I had to name anything the "co-yoneda lemma", then to avoid confusion it would be the formally dual statement.)You see, the real point of all this, to me, is that the term "co-yoneda lemma" is somewhat unnecessary (and slightly misleading) pedantry. The Yoneda lemma is of such central importance that I think one should take a correspondingly broad point of view on what it stands for. I'm suggesting that philosophically, it is healthy to view "Yoneda lemma" as standing for, a rubric for, a closely-knit circle of ideas which at one high-ish level says that homs are unit bimodules. The point I want to make is that we should be trying to get across a high level POV on what it's all about [we don't shy away from presenting high-level POVs on other things!], and calling it "co-yoneda lemma" introduces a distinction not all that needed, not terribly useful or helpful, and possibly a bit confusing. Rather, I'd emphasize the basic cohesive unity, the inner meaning of the idea, by merging the essential contents of co-yoneda lemma into the page yoneda lemma -- a separate page is not needed, and as far as I know no one has ever called it that except a few people at the n-Lab or in a small Cafe exchange.
Anyway, that's my opinion. (You asked for it, and you got it!)
-
- CommentRowNumber14.
- CommentAuthorMike Shulman
- CommentTimeNov 23rd 2009
I guess I'm not used to applying "co-" to theorems in that way, only to definitions. For instance, I don't talk about the "co-adjoint-functor-theorem;" I just say "adjoint functor theorem" regardless of whether I'm applying it to a left adjoint or a right adjoint. I suppose I do say "comonadicity theorem" but there I'm thinking of it as a statement about comonads, rather than a dual of the monadicity theorem, i.e. as a "(co-monadicity) theorem" rather than "co-(monadicity theorem)".
I think I can see the argument you're making. I do agree, on a philosophical level, that "Yoneda-ness" is all about homs being unit bimodules. However, I don't agree that distinguishing between what I call the Yoneda and co-Yoneda lemmas is unuseful, unhelpful, or confusing. The Yoneda lemma has a precise meaning to basically all mathematicians by now, referring specifically to natural transformations out of a representable functor. Regardless of whatever relation that statement may or may not bear to anything said by Yoneda, like it or not, it's what the mathematical community means by "Yoneda lemma." I think that using "Yoneda lemma" for
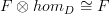 , rather than some more general term like "Yoneda-ness" or "Yoneda philosophy" or "co-Yoneda lemma" or Yoneda reduction, is gratuitously confusing. I myself would be confused if someone applied (what I call) the co-Yoneda lemma in a proof and said "by the Yoneda lemma."
, rather than some more general term like "Yoneda-ness" or "Yoneda philosophy" or "co-Yoneda lemma" or Yoneda reduction, is gratuitously confusing. I myself would be confused if someone applied (what I call) the co-Yoneda lemma in a proof and said "by the Yoneda lemma." -
- CommentRowNumber15.
- CommentAuthorTodd_Trimble
- CommentTimeNov 23rd 2009
- (edited Nov 23rd 2009)
'I myself would be confused if someone applied (what I call) the co-Yoneda lemma in a proof and said "by the Yoneda lemma."'
In view of your great sophistication, I'm surprised to hear that, especially since you agree it's (philosophically) all about unit bimodules. I'm pretty sure it wouldn't confuse me, but okay. You will agree, though, that "co-yoneda lemma" is not itself part of the general parlance, or if it already means something to anyone besides us, it's likely as the result which has been recorded in Mac Lane's CWM? As used in the nLab, it's a neologism, and a potentially confusing one since it could be taken as referring to the formal dual, or to the result in CWM. (Yes, "Yoneda reduction" is also a neologism, but not one likely to be mistaken for a different result I don't think.)
So let me then turn around and ask you: are you defending it as an optimal choice of term? (I will agree that it's not a ridiculous choice, but I've made clear why I think it has problems.)
-
- CommentRowNumber16.
- CommentAuthorTobyBartels
- CommentTimeNov 23rd 2009
Personally, I like Yoneda reduction.
-
- CommentRowNumber17.
- CommentAuthorMike Shulman
- CommentTimeNov 24th 2009
I don't think sophistication has anything to do with being confused by non-standard uses of terminology. For instance, imagine someone who says "limit" to mean "colimit," and when I object he says "well, a colimit is really just a limit in the opposite category, so I don't bother to use different terminology." I think I would still be within my rights to object. Words have meanings, sometimes they are arbitrary, but we generally stick to them in order to be able to communicate.
I'm not conscious of having invented my use of "co-Yoneda lemma;" I feel as though I read it in some paper or other. But I can't think of what that might have been, so maybe it is a neologism here. I do appreciate the confusion; although it seems clear to me what it ought to mean, evidently that is not so for everyone. I started using "co-Yoneda lemma" in this way before I encountered your use of "Yoneda reduction," and when I first encountered "Yoneda reduction", I couldn't figure out from the Yoneda reduction page on the nLab what the phrase actually meant, so I forgot about it. Now after this discussion, I've followed the link to the cafe post, which makes more sense to me.
I think I could be convinced to use "Yoneda reduction" where I have been saying "co-Yoneda lemma." Can "Yoneda reduction" refer also to the role of representable bimodules, as in an equipment? I'd also like the page Yoneda reduction to actually say precisely what is meant by "Yoneda reduction," and maybe be more explicit about it up-front too. The chatty exposition is okay, but experts shouldn't have to make their way through it to understand what is meant by the phrase.
-
- CommentRowNumber18.
- CommentAuthorTodd_Trimble
- CommentTimeNov 24th 2009
<div> <blockquote> I don't think sophistication has anything to do with being confused by non-standard uses of terminology. </blockquote> <p>Right. I think this gets back to what I was saying: in many cases (for example the very high-level description of <a href="https://ncatlab.org/nlab/show/cohomology">cohomology</a>), we at the nLab are presenting high-level points of view, in some cases recasting terms, in ways which may not have become standard yet. That's part of the evolution of mathematics. I myself feel at ease recasting the Yoneda lemma so that it reads <img src="/extensions/vLaTeX/cache/latex_34870c7ce210fb9f3e69d9a66afcbc7e.png" title="hom_D \Rightarrow_D F \cong F" style="vertical-align: -20%;" class="tex" alt="hom_D \Rightarrow_D F \cong F"/>, natural for bimodules <img src="/extensions/vLaTeX/cache/latex_9e0801eacdd43ef2a4b101146e67db98.png" title="F: C \to D" style="vertical-align: -20%;" class="tex" alt="F: C \to D"/>. That to me really <em>is</em> the Yoneda lemma, written in slicked-up form. An equivalent way of saying it is that homs are unit bimodules. It's not how I would present the Yoneda lemma to a beginner, but that's another story.</p> <p>Let me give another example: the Poincare-Birkhoff-Witt theorem. Now, there are <em>lots</em> of ways people have dreamed up of saying what is the content of this theorem, some relatively low-level, some high-level. There are definite differences between the various statements, some involving graded algebras, some involving coalgebras, but however people say it, they don't change the name of the theorem just because one version may be better known than another. They keep the same name, but express it from different angles. The higher-level versions I wouldn't choose to expose to a beginner necessarily, but that's another story.</p> <p>Thanks for your feedback on Yoneda reduction! I'll get back to that soon and clean it up. But I'll probably need a few days, as Thanksgiving is looming and other things must come first. Very nice article on equipments by the way, and there's a bunch of stuff I'd like to discuss with you some day on formal category theory.</p> </div> -
- CommentRowNumber19.
- CommentAuthorTodd_Trimble
- CommentTimeNov 24th 2009
Another case in point: the notation
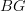 . This is something that definitely confused me! I didn't like the fact that this notation was now being reappropriated to refer to a group
. This is something that definitely confused me! I didn't like the fact that this notation was now being reappropriated to refer to a group 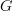 seen as a 1-object category, instead of a space. Words mean something! But I think you (Mike) and a few others tried to change my point of view on this, and I think a similar dynamic is playing out with respect to Yoneda lemma. It seems to me this is a fair comparison.
seen as a 1-object category, instead of a space. Words mean something! But I think you (Mike) and a few others tried to change my point of view on this, and I think a similar dynamic is playing out with respect to Yoneda lemma. It seems to me this is a fair comparison. -
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeNov 24th 2009
- (edited Nov 24th 2009)
Concerning
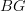 : the point we made was that in
: the point we made was that in 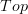 the
the 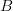 is the symbol used for delooping, and that therefore it should be used accordingly in other contexts, too.
is the symbol used for delooping, and that therefore it should be used accordingly in other contexts, too.In the category Top, this is the ordinary classifying space construction. So there is no re-interpretation here. The same operation in ooGrpd, though, means passing to the one-object groupoid. We get from the delooping object in oGrpd -- the one object groupoid -- to the delooping object in Top -- the classifyin space -- by applying the (Quillen or (oo,1)-) equivalence between the two, which is given by geometric realization
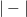 .
.(You of course konw this, I am just saying it to amplify the ingredients of the situation.)
So we take the symbols
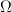 and
and 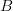 in
in 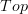 , see how they are defined abstractly there, and then apply this abstract definition more widely, as in loop space object.
, see how they are defined abstractly there, and then apply this abstract definition more widely, as in loop space object.I think this makes a lot of good sense, and that only this point of view puts some usage of "classifying space" in the literature in its correct perspective. For instance what is called the classifying space of a groupoid is nothing but the result of applying geometric realization directly to the groupoid. This is conceptually quite different from first passing from a group to a one-object groupoid and only then taking geoemtric realization and in particular does does not have any relation to the
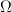 -operation.
-operation.For that reason in parts of the literature the classifying space of a groupoid
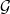 is not denoted
is not denoted 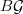 but
but 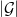 . So the established literature does not follow a globally consistent notation. In view of that I think it is sensible to pick of the existing notations that which is conceptually most sensible.
. So the established literature does not follow a globally consistent notation. In view of that I think it is sensible to pick of the existing notations that which is conceptually most sensible.I should add that at the nLab we are not the only ones using notation this way. Writing B for delooping of categories is quite wide-spread by now in the extended TQFT literature. And as John Baez once remembered, it was advocated in his article with Jim Dolan, even, where essentially the argument I just recalled is given.
For that reason I don't find our use of
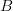 on the lab to be more a choice between existing conventions than an invention on our part.
on the lab to be more a choice between existing conventions than an invention on our part.We should maybe add a discussion along these lines to some entry: we are not re-interpreting the B-operation in Top. We just happen to find it useful to look at it frequently in the equivalent context ooGrpd.
-
- CommentRowNumber21.
- CommentAuthorTodd_Trimble
- CommentTimeNov 24th 2009
- (edited Nov 24th 2009)
Thanks, Urs. Yes, I agree entirely; I was simply using the example to illustrate a point in my discussion with Mike: that we sometimes feel free to change or stretch the scope of a notation or concept or (even a result with someone's named attached, cf. PBW) beyond what had once been considered the standard, to put it in better or higher-level perspective. But extra amplification on BG can never hurt!
-
- CommentRowNumber22.
- CommentAuthorUrs
- CommentTimeNov 24th 2009
<div> <blockquote> Yes, I agree entirely </blockquote> <p>Oh, I see, I misunderstood your comment then. I thought you meant to say that our use of B was a generalization (too) hard to swallow.</p> <p>Okay, then, maybe I copy part of such a reply over to <a href="https://ncatlab.org/nlab/show/delooping">delooping</a> later.</p> </div> -
- CommentRowNumber23.
- CommentAuthorMike Shulman
- CommentTimeNov 25th 2009
I meant to convey before that I'm perfectly happy saying that
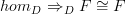 is the Yoneda lemma. But although saying that is fairly trivially equivalent to saying
is the Yoneda lemma. But although saying that is fairly trivially equivalent to saying 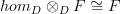 , I'm not yet happy to extend the term "Yoneda lemma" to the latter statement, because the equivalence of the two requires a fairly abstract context and their intuitive/concrete content is quite different.
, I'm not yet happy to extend the term "Yoneda lemma" to the latter statement, because the equivalence of the two requires a fairly abstract context and their intuitive/concrete content is quite different.The comparison to
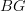 is interesting; I need to think on that a bit. It is definitely more intuitive for me to write
is interesting; I need to think on that a bit. It is definitely more intuitive for me to write 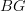 for a groupoid than to call
for a groupoid than to call 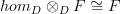 the Yoneda lemma, since I long ago internalized the fact that groupoids are the same as homotopy 1-types. But evidently the reverse is true for you!
the Yoneda lemma, since I long ago internalized the fact that groupoids are the same as homotopy 1-types. But evidently the reverse is true for you!
1 to 23 of 23