nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorTobyBartels
- CommentTimeNov 22nd 2009
I started algebraic category, with a note also at monadic adjunction.
-
- CommentRowNumber2.
- CommentAuthorTobyBartels
- CommentTimeDec 18th 2009
Now also equationally presented category.
-
- CommentRowNumber3.
- CommentAuthorTobyBartels
- CommentTimeDec 18th 2009
- (edited Dec 18th 2009)
And finitary functor.
Whose terminology is better: Johnstone's or AHS's? This infects the entire subject.
-
- CommentRowNumber4.
- CommentAuthorTobyBartels
- CommentTimeDec 18th 2009
I thought of some better terminology for quasi-equationally presentable categories. But I am pretty much throwing in my lot with AHS.
-
- CommentRowNumber5.
- CommentAuthorMike Shulman
- CommentTimeDec 19th 2009
I've never encountered the AHS version of "finitary functor." Until today I thought that "finitary" = "preserving filtered colimits" was universal. It certainly seems to me to be the most useful notion in general. Who else uses the AHS version? Are there important examples which satisfy the one but not the other?
-
- CommentRowNumber6.
- CommentAuthorTobyBartels
- CommentTimeDec 19th 2009
- (edited Dec 19th 2009)
Good question!
The only thing that AHS does with finitary functors is to characterise finitary varieties and quasivarieties of algebras. (Both of these are specified by a small set of finitary operations and laws; for a variety the laws must be equations, but for a quasivariety the laws may also have finitely many equations as hypotheses.) We want to say that a concrete category is [equivalent to the category of algebras of] a finitary (quasi)variety iff its forgetful functor is both finitary and (for a variety) monadic or (for a quasivariety) algebraic (in their sense). In the monadic case, it makes no difference; the two conditions are equivalent. But in the more general algebraic case, they are not, and only AHS's definition gives them the result that they want.
I would like a nice clean counterexample, but the only one that they give is Exercise 24A(b): ‘Let
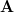 be the epireflective hull of all finite abelian groups in
be the epireflective hull of all finite abelian groups in 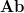 and let
and let 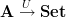 be the associated forgetful functor. Show that
be the associated forgetful functor. Show that 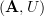 is a finitary quasivariety, but that
is a finitary quasivariety, but that 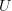 does not preserve directed colimits. [Hint: Consider the directed diagram of all finite subgroups of
does not preserve directed colimits. [Hint: Consider the directed diagram of all finite subgroups of 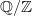 .]’
.]’While AHS demonstrate the value of their notion of ‘algebraic’ by looking at algebaic functors over many categories other than
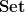 , they do not do this for their notion of finitary functor. (They do not even consider such questions as whether topological groups are finitary over topological spaces, for example.) So maybe it is not really a useful notion in general.
, they do not do this for their notion of finitary functor. (They do not even consider such questions as whether topological groups are finitary over topological spaces, for example.) So maybe it is not really a useful notion in general. -
- CommentRowNumber7.
- CommentAuthorMike Shulman
- CommentTimeDec 20th 2009
I would be surprised if the weaker notion of "finitary" were of much use over categories other than Set (although I've been surprised before). How would you feel about coming up with a different word for it? Maybe "quasi-finitary" to go along with "quasi-variety"?
-
- CommentRowNumber8.
- CommentAuthorTobyBartels
- CommentTimeDec 20th 2009
The ‘quasi’ in ‘quasivariety’ is quite analogous; in particular, a quasivariety's forgetful functor might well be finitary in the stricter sense without the quasivariety's being (even equivalent to) a variety.
I was more expecting someone to argue that AHS's term ‘algebraic’ should be changed to ‘quasi-algebraic’, which would be quite analogous, but nobody has argued for that, so that's OK.
At this point, I would be happy just to write down the usual definition of ‘finitary’, then add a note that AHS does something different and why. I'll do that at finitary functor now.
-
- CommentRowNumber9.
- CommentAuthorTobyBartels
- CommentTimeDec 20th 2009
Of course, if there is more to say about finitary functors, then it should be said there, which will probably require the page to be redesigned entirely. It's just that I don't know it; I'm really only writing this stuff because I'm going through Stone Spaces and decided to check The Joy of Cats for further understanding, leading me to spend most of my time on straightening out the terminology. The subject is more in the latter book's line than the former's, so I've been leaning towards its terminology, but that may not be wise.
-
- CommentRowNumber10.
- CommentAuthorMike Shulman
- CommentTimeDec 20th 2009
I'd be happy to change AHS's "algebraic" to "quasi-algebraic" too.
-
- CommentRowNumber11.
- CommentAuthorTobyBartels
- CommentTimeDec 20th 2009
- (edited Dec 20th 2009)
Why? Is Johnstone's language established? Is AHS's concept not useful? (Unlike their finitary functors, they do a lot with their algebraic functors.) The category of cancellative monoids (for example) is certainly finitary algebraic in a naïve sense (although so is the category of fields).
-
- CommentRowNumber12.
- CommentAuthorMike Shulman
- CommentTimeDec 20th 2009
I didn't say I had a positive reason to do it, just that I'd be happy with it. I don't really have strong feelings. I've definitely seen Johnstone's use of "algebraic" elsewhere, but I don't think it's as common as his use of "finitary" (I could be wrong though). But I think "monadic over Set" is unambiguous and not noticeably more awkward.
I myself would probably not give "algebraic" any precise meaning at all, due to the potential for confusion. But if we're going to give it a precise meaning, then AHS's seems as good as any to me.
-
- CommentRowNumber13.
- CommentAuthorTobyBartels
- CommentTimeDec 24th 2009
OK, then if you're happy with finitary functor now, then we're OK. We just have to watch out for the ambiguity of ‘algebraic’.
-
- CommentRowNumber14.
- CommentAuthorMike Shulman
- CommentTimeDec 24th 2009
Looks good.
1 to 14 of 14