nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
Atrium > Mathematics, Physics & Philosophy: A question on derived functors
Bottom of Page1 to 8 of 8
-
- CommentRowNumber1.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 8th 2009
Let me apologize for being extremely vague in formulating this question. If F: C --> D is a functor, its left derived functor LF (if it exists) is the right Kan extension of F along the projection C --> Ho(C). Yet, I could think of weak equivalences on C as a first approximation of an (infinity,1)-category structure on C, which I will denote C(infinity) just to fix the notations, and the functor F as a functor between quasi-categories N(F): N(C) --> N(D), where N denotes the nerve. Since C(infinity) is roughtly obtained from C by adding more cells in addition to commutative diagrams, I expect to have a natural inclusion functor N(C) --> C(infinity), and I can wonder about the existence of a right Kan extension of N(F) along the inclusion. This should, at least naively, correspond to taking the best infinity-approximation of F, and I'd like to think to it as a version of LF which "remembers" all higher homotopies. How far is this way of thinking from being correct? -
- CommentRowNumber2.
- CommentAuthorMike Shulman
- CommentTimeDec 8th 2009
It seems to me that it should be mostly correct. A Kan extension of
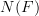 itself along
itself along 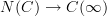 will factor through the quotient map
will factor through the quotient map 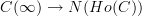 , since
, since 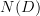 is an ordinary category, and therefore it will be just (the nerve of) the ordinary derived functor of F composed with the quotient map
is an ordinary category, and therefore it will be just (the nerve of) the ordinary derived functor of F composed with the quotient map 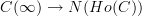 , and thus not containing any "higher information". But probably what you really want is to take the Kan extension of the composite
, and thus not containing any "higher information". But probably what you really want is to take the Kan extension of the composite 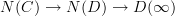 along
along 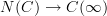 ; that ought to remember the higher homotopies. But I don't know whether this is written down anywhere.
; that ought to remember the higher homotopies. But I don't know whether this is written down anywhere. -
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeDec 8th 2009
do I understand you correctly, that you want C(infinity) to denote the simplicial localization of the category with weak equivalences C?
I suppose you have seen the query box discussion at derived functor?
Allow me to assume that we have a bit more information than just weak equivalences available, namely a nice model category structure. Then the (oo,1)-category presented by C is the simplicial localization restricted to the cofibrant-fibrant objects (as described by the Dwyer-Kan theorem recalled by the big diagram at (infinity,1)-categorical hom-space).
Typically the functors that are of interest respect this simplicial enrichement. As Mike desribes in the query box at derived functor, in that case the "correct" extension of F to the (oo,1)-category presented by C is its restriction as a simplicially enriched functor to the fibrant-cofibrant objects (or equivalently its precomposition with a fibrant-cofibrant replacement functor).
-
- CommentRowNumber4.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 9th 2009
thanks. I indeed had looked at the query box, but had been unable to read Mike's comment on the precomposition with fibrant-cofibrant replacements as an extension to the (oo,1)-category presented by C, which was precisely what I was aiming to. as far as concerns C(infty), by that I intended to mean the simplicial localization of the category with weak equivalences C, or -if that was needed in order to make things work- the (oo,1)-category presented by a model category structure on C. so Urs perfectly answer my question, and aslo Mike correctly interpret I was implicitly referring to the extension of N(C) --> D(oo) along N(C)--> C(oo).
so, going back to the derived functor query box and summing up with what's written here, the situation should be as follows:
i) one can define a notion of derived functor of F: C--> D as soon as a notion of homotopy category Ho(C), an so as soon one has a notion of weak equivalence. it is (if it exists) the Kan extension of F along C --> Ho(C).
ii) in particular, when also D has weak equivalences one can consider the derived functor LF: Ho(C) --> Ho(D) whih is by definition the extension of the composition C --> D --> Ho(D) along C--> Ho(C) (if it exists)
iii) this notion seems however to be too weak to be of concrete use (Mike's comment, if I don't misunderstand it), and the useful notion is obtained when C is a model category. In this case one can consider the extension of F to a functor F(oo): C(oo) --> D(oo). taking pi_0's one obtains LF:Ho(C) --> Ho(D). -
- CommentRowNumber5.
- CommentAuthorMike Shulman
- CommentTimeDec 9th 2009
C doesn't have to be a model category in order to go to the infinity-case; any category with weak equivalences has a simplicial localization. What you need a model category for (or, more generally, a deformation retract of a homotopical category) is to define derived functors in the "useful" way as being given by precomposition with a "replacement" functor, rather than in the "un-useful" way as a Kan extension.
-
- CommentRowNumber6.
- CommentAuthorHarry Gindi
- CommentTimeDec 9th 2009
Kan extensions are "un-useful" in what way? -
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeDec 9th 2009
<div> <blockquote> Kan extensions are "un-useful" in what way? </blockquote> <p>As a way of characterizing derived functors. See the query box discussion at <a href="https://ncatlab.org/nlab/show/derived+functor">derived functor</a>.</p> </div> -
- CommentRowNumber8.
- CommentAuthorMike Shulman
- CommentTimeDec 9th 2009
If you know of any theorems about derived functors, defined as Kan extensions without making use of the fact that in good cases (such as model categories) they can be computed with fibrant/cofibrant replacement, or even of any theorem about a particular derived functor which uses the fact that it is a Kan extension, I'd be interested to hear it. The only thing I can think of which comes close is the fact that a given functor has at most one left derived functor, independent of whatever model structure you choose to compute it with, but that can also just as easily be proven directly.
1 to 8 of 8