nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeDec 17th 2009
created bifibration
-
- CommentRowNumber2.
- CommentAuthorMike Shulman
- CommentTimeDec 18th 2009
- (edited Dec 18th 2009)
I think that the pushforward in a bifibration should be called $$f_$$, not
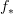 , because it is left adjoint to the pullback
, because it is left adjoint to the pullback 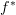 rather than right adjoint. Also in many bifibrations there is also a right adjoint to
rather than right adjoint. Also in many bifibrations there is also a right adjoint to 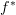 , which it makes more sense to call
, which it makes more sense to call 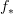 , although that adjoint is not concisely describable in fibrational language.
, although that adjoint is not concisely describable in fibrational language. -
- CommentRowNumber3.
- CommentAuthorMike Shulman
- CommentTimeDec 18th 2009
Huh, that's supposed to say f_!, but for some reason it isn't parsing correctly.
-
- CommentRowNumber4.
- CommentAuthorzskoda
- CommentTimeDec 18th 2009
I personally agree and use that convention. Benabou-Raubaud use $f_*$ as well as many algebraic and categorical treatments (maybe even Borceux but have no time to check now). I prefer the way Mike suggests, it clicks the right way at least for us who do something between algebra and geometry.
-
- CommentRowNumber5.
- CommentAuthorzskoda
- CommentTimeDec 18th 2009
- (edited Dec 18th 2009)
-
- CommentRowNumber6.
- CommentAuthorMike Shulman
- CommentTimeDec 18th 2009
You used
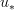 in domain cofibration, so I fixed it to u_!.
in domain cofibration, so I fixed it to u_!.I also feel strongly that "cofibration" is the wrong word here. Cofibrations have an extension property, but "cofibered categories" still have a lifting property. So "opfibration" is better. I know that Grothendieck used "cofibration" but I maintain that he should have known better.
-
- CommentRowNumber7.
- CommentAuthorzskoda
- CommentTimeDec 18th 2009
- (edited Dec 18th 2009)
Thanks Mike. I added Pierre Gabriel and references to group scheme (the latter are a subset of tyhe references at algebraic group, I ommitted those which are mainly about algebraic groups in narrow sense and variety techology and not about general group schemes and scheme language). Chanegs to several related items. I do not know of the bio data of Pierre Gabriel (strange enough, the wikipedia has so many irrelevant French and Swiss mathematicians covered but not a person of his stature...).
-
- CommentRowNumber8.
- CommentAuthorzskoda
- CommentTimeDec 18th 2009
- (edited Dec 18th 2009)
I changed the title to domain opfibration as Mike suggested. On the other hand I changed back the u_! to u_* in THAT entry.
Unlike the case of codomain fibration, where I agreed with Mike that left adjoint to u^* should be called u_!, and NOT u_*, in the case of domain cofibration we can have right adjoint of u_* which is NOT u^* but u^!, at least in geometry. Thus one has u_! -| u^* -| u_* -| u^! as in algebraic geometry (in the cases when these functors exist). If you want to have one and the same notation for all bifibration then you do not fit the examples, I prefer to fit the examples with the respective standard which is in geometry self-consistent.
To say differently, you can call a direct image in a co/opfibration either f_* or f_!, DEPENDING ON CONTEXT, however, once the context dictates one of them then you have no choice between f^* and f^! as the left versus right adjointness solely dictates the choice.
-
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeDec 18th 2009
maybe I am mixed up:
Isn't the functor
![dom : [I,C] \to C dom : [I,C] \to C](/extensions/vLaTeX/cache/latex_007f6ebf381f0c580b3d4dbf1e184232.png) the one classified by
the one classified by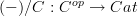
and hence a fibration? I would have thought it's the codomain functor
![codom : [I,C] \to C codom : [I,C] \to C](/extensions/vLaTeX/cache/latex_a83bd03b83583f86821385ea98f6ae98.png) that is an opfibration, as it is classified by
that is an opfibration, as it is classified by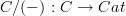
-
- CommentRowNumber10.
- CommentAuthorzskoda
- CommentTimeDec 18th 2009
- (edited Dec 18th 2009)
Urs, the fibration which is emphasised in domain fibration is about the pullback which is the usual INVERSE image. You obviously talk about the secondary cofibration structure via post-composition. I mean both are bifibrations but one strcuture is emphasised and that one is giving the name to (co)cartesian morphisms. (Co)cartesian arrows in these are exactly upper arrows of (co)cartesian squares in C.
-
- CommentRowNumber11.
- CommentAuthorzskoda
- CommentTimeDec 18th 2009
Urs notices that while the codomain fibration requires (to be a fibration) pullbacks, the cofibration part (though it did not play the same historical role) of the SAME functor does not need anything. We could in fact talk about historically motivating examples of codomain fibration and domain cofibration, as I listed, but also of "obvious" domain fibration and codomain cofibration which are used in treatment of sieves and cosieves for Grothendieck (co)topologies.
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeDec 18th 2009
I have now added plenty of "pedagogical" details to codomain fibration.
I also linked to it in the respective example-sections at overcategory and at bifibration.
-
- CommentRowNumber13.
- CommentAuthorMike Shulman
- CommentTimeDec 18th 2009
Okay, I'll go along with u_* and u^! for domain opfibration, but I added some explanation as to why it's different from the usual notation for bifibrations. (Why doesn't u_! work in latex on the forum?)
-
- CommentRowNumber14.
- CommentAuthorDavid_Corfield
- CommentTimeMay 5th 2018
-
- CommentRowNumber15.
- CommentAuthorDavid_Corfield
- CommentTimeJun 27th 2018
- (edited Jun 27th 2018)
We have a section called ’Remark’ which has only
A bifibration such that is a bifibration as well is called a trifibration (cf. Pavlović 1990, p.315).
As this MO comment observes, it’s rather misleading. In that paper by Pavlović it says
We say that is a trifibration if both and are bifibrations. The category , fibred over , is obtained by changing the direction of all the vertical arrows in . (The arrows of are the equivalence classes of spans with a vertical arrow pointing at the source, and a cartesian arrow pointing at the target.)
A fibration is a bifibration iff every inverse image functor has a left adjoint . It is a trifibration iff there is also a right adjoint .
It sounds like it’s due its own page, so I’ll start one.
-
- CommentRowNumber16.
- CommentAuthorMike Shulman
- CommentTimeJun 27th 2018
I moved the “Remark” with link to trifibration into the Related Concepts section.
-
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeMay 5th 2023
-
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeMay 5th 2023
reworded the paragraph on bifibrations of model categories that used to be a sub-section of its own and made it a remark here pointing instead to Grothendieck construction for model categories for details
-
- CommentRowNumber19.
- CommentAuthorBryceClarke
- CommentTimeMay 5th 2023
- (edited May 5th 2023)
The part of the entry on “Relation to distributive laws” should be moved to two-sided fibration; the use of the term “bifibration” used here is not consistent with the rest of the entry.
I was also wondering if there is an original reference where bifibrations were defined; I imagine this might be the same place where Grothendieck fibrations were defined.
-
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeMay 5th 2023
should be moved
Please do! If you have the energy.
-
- CommentRowNumber21.
- CommentAuthorUrs
- CommentTimeMay 5th 2023
Regarding the question concerning original references:
I haven’t spotted bifibrations in Grothendieck’s “Technique de descente…”, but they are introduced very clearly and with that terminology (up to translation) in:
- Alexander Grothendieck, Catégories co-fibrées, catégories bi-fibrées., Section 10 in exposé VI of: Revêtements Etales et Groupe Fondamental - Séminaire de Géometrie Algébrique du Bois Marie 1960/61 (SGA 1), LNM 224 Springer (1971) [updated version with comments by M. Raynaud: arxiv.0206203]
A few years later Gray’s text speaks of “functors that are both fibrations as well as opfibrations” but does not call them “bifibrations”:
- John W. Gray, pp. 59 of: Fibred and Cofibred Categories, in: S. Eilenberg, D. K. Harrison, S. MacLane, H. Röhrl (eds.): Proceedings of the Conference on Categorical Algebra - La Jolla 1965, Springer (1966) 21-83 [doi:10.1007/978-3-642-99902-4]
(Have added these to the entry here.)
Incidentally, I don’t see bifibrations (or even opfibrations) mentioned at all in Bénabou 1985 which makes me suspect that they are also not mentioned in Bénabou 1975 but I don’t have a useful enough copy of the latter to bother checking
-
- CommentRowNumber22.
- CommentAuthorUrs
- CommentTimeMay 5th 2023
- (edited May 5th 2023)
Deleted the reference to Buckley (fibrations of 2-categories) and instead added a disambiguation warning to the top of the entry.
Will create now fibration of 2-categories to have this sorted out.
[edit: Oh, now I see that this is already redirecting to somewhere :-)]
-
- CommentRowNumber23.
- CommentAuthorUrs
- CommentTimeMay 6th 2023
deleting the subsection on “Relation to distributive laws” and the reference to von Glehn 2015, moving both to two-sided fibration
-
- CommentRowNumber24.
- CommentAuthorUrs
- CommentTimeMay 6th 2023
- (edited May 6th 2023)
added pointer to:
- Bart Jacobs, Lem. 9.1.2 of: Categorical Logic and Type Theory, Studies in Logic and the Foundations of Mathematics 141, Elsevier (1998) [ISBN:978-0-444-50170-7, pdf]
for the statement that a fibration is a bifibration iff all its base change functors have an adjoint on the appropriate side.
1 to 24 of 24