nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeJan 7th 2010
- (edited May 6th 2015)
following up on our discussion in the thread <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=593&page=1#Item_12">oo-vector bundle (forum)</a> here on the forum, I have now spent a bit of time on expanding the entry quasicoherent sheaf
- I fixed the formulas in the section <a href="http://ncatlab.org/nlab/show/quasicoherent+sheaf#AsSheaves">As sheaves on Aff/X</a>. They were a bit rough and typo-ridden in the first version (which likely was my fault, not anyone else's). Since there are 50 variants in the literature to state this, I also pointed to page and verse in a lecture by Goerss where the statement is given explicitly the way it now appears there in the entry
- then I added a new section <a href="http://ncatlab.org/nlab/show/quasicoherent+sheaf#AsSheaves">As homs into the stack of modules</a> where I aim to describe in great detail how this definition is equivalent to the even simpler one, where we just say that the category of quasicoherent sheaves on a sheaf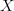 is the Hom-category
is the Hom-category 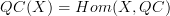 for
for 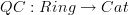 the stack of modules, classifying the canonical bifibration
the stack of modules, classifying the canonical bifibration 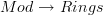 . This is the statement that my discussion at <a href="http://ncatlab.org/schreiber/show/%E2%88%9E-vector+bundle">oo-vector bundle (schreiber)</a> was secretly based on, which I promised to make more explicit.
. This is the statement that my discussion at <a href="http://ncatlab.org/schreiber/show/%E2%88%9E-vector+bundle">oo-vector bundle (schreiber)</a> was secretly based on, which I promised to make more explicit.
- then I added a section <a href="http://ncatlab.org/nlab/show/quasicoherent+sheaf#Higher">Higher/derived quasicoherent sheaves</a>, where I indicate the now obvious oo-categorification discussed in more detail at <a href="http://ncatlab.org/schreiber/show/%E2%88%9E-vector+bundle">oo-vector bundle (schreiber)</a> and point out how this gives the derived QC sheaves used by Ben-Zvi et al as discussed at geometric infinity-function theory
- finally I wrote a fairly detailed <a href="http://ncatlab.org/nlab/show/quasicoherent+sheaf#Idea">Idea</a> section for quasicoherent sheaves, that previews the content of all these sections. -
- CommentRowNumber2.
- CommentAuthorzskoda
- CommentTimeJan 7th 2010
- (edited Jan 7th 2010)
Taking Hom category is Yoneda strictification, and as I pointed out many time (and emphasised in Rosenberg-Kontsevich), this is taking quasicoherent sections of a fibered category of O-modules. What you describe (Kan extension) is a standard way to extend a stack to the category of presheaves, though I may not understand some aspects of your approach. For example, I do not see why do you insist on "bifibration" if the only thing used in such constructions is a fibered category structure (I also find it confusing to me talking "classifying" in this context for a pseudofunctor f*). See the section below in quasicoherent sheaf which quotes
The fibered category of O X-modules can be replaced by a more general fibered category. Then the category of quasicoherent modules in this fibered category is the category opposite to the category of cartesian sections of ...(I do not see who to cut and paste from nlab to see the special symbols!!). This viewpoint is used by Rosenberg-Kontsevich in their preprint on noncommutative stacks (dvi, ps).
If one considers a ring as a one object additive category, instead of Yoneda one can consider a similar functor explained in MacLane-Moerdijk book in the treatment of the tensor products in the chapter on geometric morphism (one of the exercises). In infinitedimensional context (ind-schemes) there are two different definition of qcoh sheaves, one agrees with this one, while another is more sensible for infinitedimensional schemes.
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeJan 7th 2010
- (edited May 6th 2015)
<blockquote>
Taking Hom category is Yoneda strictification, and as I pointed out many time, this is taking quasicoherent sections of a fibered category of O-modules.
</blockquote>
Sorry, but I don't even know what that means. What is "Yoneda strictification"? And why quasicoherent sections? The category of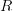 -modules is the category of all sections of
-modules is the category of all sections of 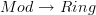 over
over 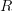 . So I am not sure what you are referring to.
. So I am not sure what you are referring to.
But let me just know: do you agree, or not, that for a scheme, regarded as a sheaf on Aff, and for
a scheme, regarded as a sheaf on Aff, and for 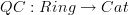 the functor that classifies
the functor that classifies 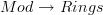 that the category of quasicoherent sheaves on
that the category of quasicoherent sheaves on  is the hom-category of morphisms
is the hom-category of morphisms 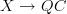 .
.
I try in the entry to spell out explcitly why this is true. Possibly there is a mistake in my derivation. Let me know if you think there is a flaw. -
- CommentRowNumber4.
- CommentAuthorzskoda
- CommentTimeJan 7th 2010
- (edited Jan 7th 2010)
The category of R-modules is the category of all sections of Mod \to Ring over R.
Well but this is NOT the category of O-modules. This input is already strictified. When you do Kan extension you are simultaneously doing extension to a bigger category and strictification. The starting category over a category does not need even to be fibered, this follows in general.
Please do not use term "classifies" for what is traditionally called cleavage, it confuses me, each time (as classifying has so many other meanings which I do use). I am not saying that there is an error, but I think you chose a complicated way using all these end formulas to say a special case of something what is much simpler in fibered category setup.
Look at page 1 and page 4 of the Kontsevich-Rosenberg paper Also look at 1.1.5 how one gets the special case inducing qcoh modules one the category of presheaves, which corresponds to your case. Quasicoheretor which I mentioned yeterday is the right adjoint from 1.1.3.
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeJan 7th 2010
- (edited May 6th 2015)
<blockquote>
Well but this is NOT the category of O-modules.
</blockquote>
So you are tinking of some fibration such that its "quasicoherent sections" are O-modules. Which fibration is that and what's the definition of "quasicoherent section"?
<blockquote>
Please do not use term “classifies” for what is traditionally called cleavage,
</blockquote>
What I mean is the Grothendieck construction. Does one say "cleavage" for Grothendieck construction?
Anyway, I mean the functor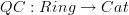 that is given by
that is given by 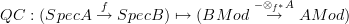 .
.
And you are right that I maybe shouldn't be talking about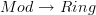 as being a bifibration, even though it is, because all I need is that it is a fibration, yes.
as being a bifibration, even though it is, because all I need is that it is a fibration, yes.
-
- CommentRowNumber6.
- CommentAuthorzskoda
- CommentTimeJan 7th 2010
- (edited Jan 7th 2010)
o you are tinking of some fibration such that its "quasicoherent sections" are O-modules.
Urs, no. Sheaves of O-modules are not necessarily quasicoherent. They can have unpredictable bumps, as I explained before. Quasicoherent sheaves on schemes is just a short for "quasicoherent sheaves of O-modules". Now there is a forgetful functor from quasicoherent sheaves of O-modules to just O-modules which has a right adjoint, the quasicoheretor functor, which is well explained in Orlov's paper listed in the nlab article.
A cleavage of a fibered category is A CHOICE of inverse image pseudofunctor, given a fibered category, it is not unique and we need axiom of choice to find it. This is definitely not Grothendieck construction, the Grothendieck construction is the inverse: getting from a pseudofunctor to a fibered category. One can start with a category over a category, but such that it is not fibered. From that one can make a pseudofunctor as well, and then perform the Grothendieck construction, the composition is the big Lim (= bicategorical colim) of the original category of a category as a functor. This is a strictification equal to taking opposite of the category of qcoh sections. A third related construction is Street's first strictification which starts with a pseudofunctor but produces strict functor (thus one has a splitting instead of just a cleavage).
Yet another warning: the idea section starts with a notion of qcoh sheaf on a locally ringed space. Later at some point somebody wrote that this can be interpreted via sheaf theortical nonsense, on presheaves of sets etc. This is true ONLY if the locally ringed space is locally affine and the topology is of rather special type, generated by affine maps, otherwise we can not view it as a sheaf on the affines in a subcanoncial topology.
In infinite-categorical situation one could take again qcoh sections for any left fibration of quasicategories what is more general than taking homs in special kind of objects which you call QC.
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeJan 7th 2010
- (edited Jan 7th 2010)
<div> <blockquote> Yet another warning: the idea section starts with a notion of qcoh sheaf on a locally ringed space. Later at some point somebody wrote that this can be interpreted via sheaf theortical nonsense, on presheaves of sets etc. This is true ONLY if the locally ringed space is locally affine and the topology is of rather special type, </blockquote> <p>So the statement in the section</p> <p><a href="http://ncatlab.org/nlab/show/quasicoherent%20sheaf#AsSheaves">As sheaves over Aff/X</a></p> <p>needs to state more conditions on <img src="/extensions/vLaTeX/cache/latex_04d0eb37f084cb02c47fa2a271035fef.png" title="X" style="vertical-align: -20%;" class="tex" alt="X"/> and on the topology?</p> <p>Zoran, could you just go ahead and put into the entry precisely the statements that you say are needed. Somehow we keep talking past each other and maybe it's quicker if you write down the right version than trying to tell me to write down what you think needs to be written. :-)</p> <p>After you've done it I look at it.</p> </div> -
- CommentRowNumber8.
- CommentAuthorzskoda
- CommentTimeJan 7th 2010
- (edited Jan 7th 2010)
No, I won't do much now. I left more extensive changes for some time in future. I am already wasting too much time for nlab, and now it is much harder when there are so many additions to the entry. But if you read just 2/3 pages of Orlov and Konstevich/Rosenberg we would save all the effort we had in discussion. On Aff/X the thing is OK if Aff is what it is and the topology is Zariski. Kontsevich-Rosenberg ad other references are more careful about the topology. Note that the usual quasicoherent presheaves are automatically shevaes in Zariski case. As we talked when we talked about descent, quasicoherent presheaves KNOW what is the underlying maximal topology in a sense.
-
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeJan 7th 2010
Okay. I should make clear that I haven't found the time and energy to look into the classical theory of quaasicoherent sheaves on schemes much. I know you provided the references, and I thank you for that, but I am already doing too many things at once.
All I was focusing on here is the statement that the definition "as sheaves on Aff/X" as stated currently in the entry, characterizing pre(!)sheaves on Aff/X with a certain property of their restriction morphisms is equivalent -- purely by abstract nonsense -- to the definition in terms of morphisms of presheaves
 .
. -
- CommentRowNumber10.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 7th 2010
I'm a bit confused here. I just gave a quick look at the Rosenberg-Kontsevich paper and it seems to me less intuitive (and more general?) of the construction Urs describes. Namely, the only difficult point in Urs' approach to QC(X) seems to me the identification of [Ring,Cat](X,QC) with the Kan extension along Yoneda embedding.
On the other hand, [Ring,Cat](X,QC) is perfectly defined as soon as one considers the functor disc: Set --> Cat, and uses it to see X: Ring --> Set as a functor from Ring to Cat. And the fact that [Ring,Cat](-,QC) is an extension of QC: Ring --> Cat is just an instance of Yoneda.
So if one is solely interested in a "simple" extension of QC to arbitrary presheaves of Sets on Ring^{op}, [Ring,Cat](X,QC) would nicely do the job. And moreover one can prove, as is done in the second part of Urs' entry, that for a scheme X [Ring,Cat](X,QC) is actually equivalent to Qcoh(X) as is defined e.g., in terms of shevaes on Aff/X.
Therefore the point is that here one not only wants to extend in a way that works, but to extend in a canonical way, and such a canonical extension is provided by Yoneda extension. So one is left with the task of proving that the "nice and simple" extension [Ring,Cat](X,QC) is equivalent to Yoneda extension.
This may be not crystal clear (I've not gone into the details, yet), but should be a completely general instance of Yoneda embedding, not depening neither on Ring nor on QC. What should be true is that (maybe under suitable hypotesis), X ---> [C,Cat](X,F) is the Yoneda extension of F: C --> Cat, where X:C --> Set. -
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeJan 7th 2010
- (edited Jan 7th 2010)
I mentioned that this construction is a right Kan extension only for the record, it doesn't really matter much so far. Also that the definition by the hom of stacks exists naturally is clear. The point under discussion is how exactly this does indeed capture what is described by other means in the literature.
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeJan 7th 2010
- (edited Jan 7th 2010)
but, wait. take paragraph 1.1.5 in Kontsevich Roserberg.
They say that their definition of the cat of quasicoherent sheaves on a presheaf X on a site E with respect to fibration
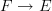 is the cat of cartesian functors
is the cat of cartesian functors 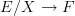 over
over 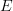 .
.Isn't that the same as the cat of morphisms
 , with
, with 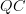 the pseudofunctor corresponding to
the pseudofunctor corresponding to 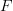 under the Grothendieck construction?
under the Grothendieck construction?Mike? Todd?
-
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeJan 7th 2010
- (edited Jan 7th 2010)
<div> <p>I wrote:</p> <blockquote> Isn't that the same </blockquote> <p>Sure it is.</p> <p>Somebody please give me a sanity check:</p> <p>Paragraph 1.1.5 in <a href="http://www.mpim-bonn.mpg.de/preprints/send?bid=2333">Kontsevich-Rosenberg</a> is nothing, I think, but the category of pseudofunctors that I am talking about -- but described under the equivalence given by the Grothendieck construction in terms of fibered categories:</p> <ul> <li><p>their <img src="/extensions/vLaTeX/cache/latex_62ee0dd9f4d9bb034c4b5a0e3fe8e324.png" title="E" style="vertical-align: -20%;" class="tex" alt="E"/> is <img src="/extensions/vLaTeX/cache/latex_b111c2e8748afb8b7665b27bea395a99.png" title=" E = Ring^{op} " style="vertical-align: -20%;" class="tex" alt=" E = Ring^{op} "/> for us</p></li> <li><p>so their <img src="/extensions/vLaTeX/cache/latex_89eabda702ae2421acfbfda451243ea5.png" title=" E/X " style="vertical-align: -20%;" class="tex" alt=" E/X "/> is nothing but the <a href="https://ncatlab.org/nlab/show/category+of+elements">category of elements</a> of the presheaf <img src="/extensions/vLaTeX/cache/latex_affd89a8cd39b956ec4d2f2a51464690.png" title=" X : Ring \to Set" style="vertical-align: -20%;" class="tex" alt=" X : Ring \to Set"/>, hence the image under the <a href="https://ncatlab.org/nlab/show/Grothendieck+construction">Grothendieck construction</a> of <img src="/extensions/vLaTeX/cache/latex_5b33586fe138ebca0c30bd0e3643f6b1.png" title=" X" style="vertical-align: -20%;" class="tex" alt=" X"/></p></li> <li><p>their <img src="/extensions/vLaTeX/cache/latex_3881474e0d8aa3b215bf05ddb6b75b5c.png" title="F \to E" style="vertical-align: -20%;" class="tex" alt="F \to E"/> is our <img src="/extensions/vLaTeX/cache/latex_2c6cb3c76d33dbbc62e82ff8c6d62089.png" title=" Mod \to Ring" style="vertical-align: -20%;" class="tex" alt=" Mod \to Ring"/>. By definition, what I wrote as <img src="/extensions/vLaTeX/cache/latex_bc5fe60f38700778e321eb1e23186169.png" title=" QC : Ring \to Cat" style="vertical-align: -20%;" class="tex" alt=" QC : Ring \to Cat"/> is the pseudofunctor corresponding to this under the Grothendieck construction</p></li> <li><p>they say the cat of quasicoherent sheaves on <img src="/extensions/vLaTeX/cache/latex_5b33586fe138ebca0c30bd0e3643f6b1.png" title=" X" style="vertical-align: -20%;" class="tex" alt=" X"/> is the category of cartesian morphisms from <img src="/extensions/vLaTeX/cache/latex_64f37e308576f3303a4923fc1ee38893.png" title=" X/E" style="vertical-align: -20%;" class="tex" alt=" X/E"/> to <img src="/extensions/vLaTeX/cache/latex_5ec3dcd4fa96727f6008946ebbeebfa2.png" title="F" style="vertical-align: -20%;" class="tex" alt="F"/> over <img src="/extensions/vLaTeX/cache/latex_62ee0dd9f4d9bb034c4b5a0e3fe8e324.png" title="E" style="vertical-align: -20%;" class="tex" alt="E"/>. But it's the very statement of the equivalence induced by the Grothendieck construction that says that this is the same as the functor category <img src="/extensions/vLaTeX/cache/latex_124bf0084d7f39958907ac76b4941d38.png" title=" X \to QC" style="vertical-align: -20%;" class="tex" alt=" X \to QC"/>: the nLab sort of says this a bit at <a href="https://ncatlab.org/nlab/show/Grothendieck+fibration">Grothendieck fibration</a> (maybe this could be made more explicit and highlighted more).</p></li> </ul> <p>I will have to go offline in a minute. But think about this. It looks to me that Rosenberg-Kontsevich make exactly my point, just viewed from the dual perspective of fibered categories.</p> </div> -
- CommentRowNumber14.
- CommentAuthorzskoda
- CommentTimeJan 7th 2010
Your analysis of Kontsevich-Rosenberg is surely correct. The simpler procedure of taking just (the opposite to) the category of cartesian sections as quasicoherent modules is fully general, not applying only to presheaves. In your case (the 1.1.5) Yoneda strictification (CARTESIAN hom into a cleavage) gives an equivalent result, both the Yoneda and coherence are taken together in one step by limiting hom to cartesian hom in Yoneda, what makes it strictified. I find it not only more general, but also easier to think and perform separately, because taking cartesian section as opposed to all sections is about strictification/coherence and Yoneda is about extending to presheaves. Each thing has its own meaning and the steps or choices are manifest; furthermore it is general and finally, it does not involve considering enriched/weighted limits, what is for most practical mathematician hardly comprehensible (I myself read lines with weighted co/limits only when forced).
-
- CommentRowNumber15.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 7th 2010
still I find Urs' [Ring,Cat](X,QC) approach very simple and appealing. The difficulty with weighted limits could be conveniently hidden into a general statement on Yoneda extension, as sketched in a post of mine above. I'll try to write out the deatils of this during the week-end (tomorrow is impossible). -
- CommentRowNumber16.
- CommentAuthorzskoda
- CommentTimeJan 7th 2010
- (edited Jan 7th 2010)
Ne entry cleavage.
Domenico: One should also point out that the morphisms of pseudofunctors (if the pseudofunctor aprpoach is taken instead of invariant fibered category approach) involve 2-cells which satisfy prescribed coherences (currently not listed in the entry, see the lecture notes on gerbes by Moerdijk for that approach). The managing of coherences instead of invariant property approach via cartesian functors is why Grothendieck and Gabriel left pseudofunctors and chose fibered categories. Try also to see how the definitions work in some other well-known cases (rather than just the (pre)sheaves of sets and simplicial sets). One good example are configuration schemes.
Urs: at your personal page it still says that the abelianization of Vect/X is the category of qcoh sheaves of modules, the correct is just coherent, as it is smaller and already abelian.
-
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeJan 7th 2010
- (edited Jan 7th 2010)
<div> <blockquote> Yoneda strictification (CARTESIAN hom into a cleavage) </blockquote> <p>Hm, sorry, I'm still not sure what you mean by this.</p> <p>The equivalence of bicategories given by the Grothendieck construction is between</p> <ul> <li><p>the bicatgeory of pseudofunctors <img src="/extensions/vLaTeX/cache/latex_34bf529d998c2b522f58576022ebfe4a.png" title=" E^{op} \to Cat" style="vertical-align: -20%;" class="tex" alt=" E^{op} \to Cat"/>, pseudonatural transformations and modifications of these</p></li> <li><p>and the bicategory of Grothendieck fibrations <img src="/extensions/vLaTeX/cache/latex_3881474e0d8aa3b215bf05ddb6b75b5c.png" title="F \to E" style="vertical-align: -20%;" class="tex" alt="F \to E"/>, cartesian morphisms between these over <img src="/extensions/vLaTeX/cache/latex_62ee0dd9f4d9bb034c4b5a0e3fe8e324.png" title="E" style="vertical-align: -20%;" class="tex" alt="E"/> and transformations between these.</p></li> </ul> <p>Isn't it? The fact that we have cartesian morphisms between the fibered categories is precisely what models that this comes from a transformations between the corresponding pseudofunctors.</p> </div> -
- CommentRowNumber18.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 7th 2010
Zoran: thanks for pointing my attention to coherencies: I'll try to work out the details and see what happens. -
- CommentRowNumber19.
- CommentAuthorzskoda
- CommentTimeJan 7th 2010
- (edited Jan 7th 2010)
Correct Urs, but in category over a category formalism the distinction is important. Your Yoneda hom can be taken in that category, rather than in the bicategory of pseudofunctors. In orbifold theory for example in 1990s people talked about wrong morphisms of orbifolds as they did not take care of cartesian property. Once they realized that they started calling such correct morphisms strong or good morphisms of orbifolds. Of course, the people working in stack language had never had that problem. But if we allow to consider categories over categories, not only stacks, then one can easily slip and not taking care of it. The two languages are precisely equivalent as you quoted.
In a pseudofunctor approach one does not need to think about non-cartesian morphism, it is rather important to keep the 2-cells involving morphisms between pseudofunctors coherent and a part of the data (not just existence).
Urs: are you still finding word quasicoherent unintuitive ?
-
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeJan 7th 2010
I added a new section As cartesian morphisms of fibrations.
I guess we agree on what I wrote there now. But have a look.
-
- CommentRowNumber21.
- CommentAuthorzskoda
- CommentTimeJan 7th 2010
I like it.
-
- CommentRowNumber22.
- CommentAuthorUrs
- CommentTimeJan 7th 2010
Okay, good. I am glad we clarified this. And I am glad that Kontsevich-Rosenberg agree with us! :-)
This is a really powerful nice abstract nonsense definition. Combined with Lurie's stuff on tangent (infinity,1)-category this gives a amazingly fundamental way of thinking about all things related to modules and vector bundles.
This is why I don't like to call this "quasicoherent sheaf", yes. It feels like calling something as fundamental as, say, the Yoneda lemma, a "quasi-something". I think that this appears as quasi-somethingelse is a historical coincidence. This stuff here is somewhere at the very bottom of the structure of math. It's fundamental and should have a more suggestive name, as such.
That's my feeling anyway, But I understand that the term "quasi--coherent" is widely accepted and does describe some aspects of this.
-
- CommentRowNumber23.
- CommentAuthorzskoda
- CommentTimeJan 7th 2010
- (edited Jan 7th 2010)
But indeed in practical everyday mathematics coherent sheaves are usually more often used than quasicoherent. But from the fundamental point of view, quasicoherent sheaves work correctly in more general situations. Coherent sheaves are good for locally noetherian schemes and for complex analytic manifolds for example, but not for nonnoetherian schemes: but quasicoherent work always. I was asking about the intuition about "coherent" part of the name (which is even better seen when looking at local sections in locally ringed space point of view). Quasi may be kind of accident. But saying vector bundle can get much harsher critique from many points of view (for example if you want to discuss infinitedimensional vector bundles in algebraic geometry properly, you need to get out of quasicoherent category as shown by Drinfeld!!). I agree that the Lurie's quasicategory tangent bundle is amazing discovery and treated in such subtle and natural detail that it is breathtaking. I am glad that you find the quasicoherent sheaves fundamental.
-
- CommentRowNumber24.
- CommentAuthorzskoda
- CommentTimeJan 8th 2010
- (edited Jan 8th 2010)
I have created a new section
- Direct definition for presheaves of sets on Aff
in quasicoherent sheaf having a direct variant of the definition (which I learned a year and half ago from the Beilinson-Drinfeld paper on Hitchin fibration, cited somewhere on the page) which is of course equivalent (quite obviously), but its explicit character makes less need to think of Grothendieck constructions, Kan extensions etc. although they are facing you directly into your eyes. I spelled unusually precisely the version of coherence for that approach which is usually not spelled out.
I hope you like it.
-
- CommentRowNumber25.
- CommentAuthorMike Shulman
- CommentTimeJan 8th 2010
Some expansion on terminology at cleavage.
-
- CommentRowNumber26.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 8th 2010
Just a rought idea (today I'll be unable to work on the lab, sorry):
consider the natural embedding CRing --> SCRing (C stands for commutative, S for simplicial). then we have the fibration SMod --> SCRing and we can hope it pulls back to Mod --> CRing. should this be so, we would be done: SMod --> SCRing is equivalent to TSCRing --> SCRing, and so Mod (and therefore Qcoh) would be completely recovered from CRing --> SCRing <-- TSCRing. -
- CommentRowNumber27.
- CommentAuthorUrs
- CommentTimeJan 8th 2010
- (edited Jan 8th 2010)
<div> <p>Zoran wrote:</p> <blockquote> I have created a new section: Direct definition for presheaves of sets on Aff </blockquote> <p>Nice, thanks. That's in fact better/more detailed than the previous section. It's good that you mention the cocycle condition. You see, this comes out out the pseudofunctor description: it's the "pseudonaturality prism" equation on triangles for a pseudonatural transformation of pseudofunctors. When I typed my proof, I was wondering why Goerss didn't mention it! Now I am glad to see that other authors to mention it. :-) So I added one more item to my discussion of the pseudonatural transformations and said that also the coycle which you mention comes out.</p> <p>I think we should eventually try to merge the new section that you added with the previous one. They are really about the same thing. Yours is more detailed, but there is also now some repetition of the statement of the context.</p> <p>Also: we need to try to harmonize and sort out what is a fibration and what is an opfibration.</p> <p>Let's see, we have the pseudofunctor <img src="/extensions/vLaTeX/cache/latex_d40c607adfb83ae73204cc3c3a4eb706.png" title=" QC : CRings \to Cat " style="vertical-align: -20%;" class="tex" alt=" QC : CRings \to Cat "/> given by <img src="/extensions/vLaTeX/cache/latex_7d363aa2a281ecaa1c1f6dc18eea6f83.png" title=" QC : (R \stackrel{f}{\to} S) \mapsto (R Mod \stackrel{-\otimes_f S}{\to} S Mod) " style="vertical-align: -20%;" class="tex" alt=" QC : (R \stackrel{f}{\to} S) \mapsto (R Mod \stackrel{-\otimes_f S}{\to} S Mod) "/>.</p> <p>By Grothendieck constructions this yields an _op_fibration</p> <p><img src="/extensions/vLaTeX/cache/latex_932e6f1e6f86908e98006ae3f69551a3.png" title=" Mod \to CRing " style="vertical-align: -20%;" class="tex" alt=" Mod \to CRing "/>,</p> <p>right? Hence a fibration <img src="/extensions/vLaTeX/cache/latex_47e3c0c9d12568a71ff5e01402433bf5.png" title=" Mod^{op} \to CRing^{op} " style="vertical-align: -20%;" class="tex" alt=" Mod^{op} \to CRing^{op} "/> .</p> <p>Of course since <img src="/extensions/vLaTeX/cache/latex_e6eac473632253fcf93de52f50ce87e6.png" title="Mod to CRing" style="vertical-align: -20%;" class="tex" alt="Mod to CRing"/> is a bifibration, there is also a fibration <img src="/extensions/vLaTeX/cache/latex_7ea7809b7b68b91e36807a2397874873.png" title=" Mod \to CRing^{op}" style="vertical-align: -20%;" class="tex" alt=" Mod \to CRing^{op}"/>, but that's not the one we need here, as you emphasized above.</p> <p>These op-things are easily mixed up. Could you give me a sanity check on the above reasoning? Once we agree on this, somenody should go through the entry and harmonize it. I think currently it is slightly inconsistent internally in notation.</p> </div> -
- CommentRowNumber28.
- CommentAuthorzskoda
- CommentTimeJan 8th 2010
I think that covariant pseudofunctor from $CRing$ is viewed as contravariant functor from $CRing^{op}$, both with target $Mod$ and not $Mod^{op}$, and one traditionally looks at the Grothendieck fibration for that contravariant functor. I do not want to change the point of view to cofibrations from $Mod^{op}$. Thus I do not want to interpret $f^*$ as direct image, it must be inverse image, and it does not matter weather downstairs I label morphism of rings or opposite, of affine spectra. Relabelling changes covariant to contravariant, but I still talk about inverse images. This is quite usual, having "covariant" fibrations.
-
- CommentRowNumber29.
- CommentAuthorUrs
- CommentTimeJan 8th 2010
I see, okay. Maybe we should make this explicit at the entry.
-
- CommentRowNumber30.
- CommentAuthorUrs
- CommentTimeJan 8th 2010
- (edited Jan 8th 2010)
I edited coherent sheaf a bit, trying to prettify it.
I also mention quasicoherent sheaves there, now. And at quasicoherent sheaf I edited the first definition paragraph, especially where it refers to coherent sheaves.
I think there was an inaccuracy in the previous verision: it had said that if the
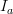 and
and 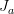 can be chosen finite, then the sheaf is coherent. But this is only true of the structure sheaf itself is coherent. Right? Otherwise one has to add the "finite type" condition. Please check my edits.
can be chosen finite, then the sheaf is coherent. But this is only true of the structure sheaf itself is coherent. Right? Otherwise one has to add the "finite type" condition. Please check my edits. -
- CommentRowNumber31.
- CommentAuthorUrs
- CommentTimeJan 8th 2010
- (edited Jan 8th 2010)
I wrote something at free module, to satisfy that link, but I am in a haste now.
I also saw now Toby's query box at what is now free construction > history. I made "free construction" instead redirect to free functor.
I quickly added in the link to free module in the examples section at free functor, but it's a bit rough there now. If nobody else does, I'll polish it later.
-
- CommentRowNumber32.
- CommentAuthorzskoda
- CommentTimeJan 11th 2010
Let me speculate a bit: there is Giraud's reconstruction from given Grothendieck topos of a site which reproduced a topos; there is Rosenberg's reconstruction of a scheme, up to isomorphism, out of its category of quasicoherent sheaves. Is there a way to rediscover the essentials of the Rosenberg's reconstruction from knowing the Giraud's reconstruction and the general nonsense approach to quasicoherent sheaves ?
-
- CommentRowNumber33.
- CommentAuthorUrs
- CommentTimeDec 19th 2013
- (edited Dec 20th 2013)
added to quasicoherent sheaf a brief note on the definition for structured infinity-toposes: here
-
- CommentRowNumber34.
- CommentAuthorUrs
- CommentTimeDec 20th 2013
- (edited Dec 20th 2013)
following this, I have now added to differential cohesion a brief note here observing that (quasicoherent) sheaves of -modules are naturally axiomatized in differential cohesion.
[ there is an issue with left exactness, I may have to get back to this tomorrow, did leave a warning in the entry ]
-
- CommentRowNumber35.
- CommentAuthorUrs
- CommentTimeFeb 16th 2014
- (edited Feb 16th 2014)
What are some decent sufficient conditions for pullback of quasicoherent sheaves to have a left adjoint?
-
- CommentRowNumber36.
- CommentAuthorUrs
- CommentTimeFeb 16th 2014
Ah, never mind, I got what I was looking for, in prop. 3.3.23 of DAG XII.
(I’ll be adding this now as an example at Wirthmüller context.)
-
- CommentRowNumber37.
- CommentAuthorZhen Lin
- CommentTimeFeb 16th 2014
It’s probably instructive to work out the affine case first. The Eilenberg-Watts theorem says a left adjoint (necessarily additive) is isomorphic to a functor of the form , for some -bimodule , so a right adjoint must be isomorphic to a functor of the form for some -bimodule . Thus, if is a commutative ring homomorphism such that has a left adjoint, then for some -bimodule ; and since is a left adjoint, must be finitely presented and projective as a -module. So the same is true for .
Now suppose is finitely generated and projective as a -module. Then is a retract of a finitely generated free -module, say . Clearly, preserves limits and filtered colimits, so it has a left adjoint (by the accessible adjoint functor theorem). Thus the necessary and sufficient condition is “ is finitely generated and projective as a -module”.
A similar argument should show that has a left adjoint when is a morphism such that is locally free of finite rank as an -module.
-
- CommentRowNumber38.
- CommentAuthorUrs
- CommentTimeFeb 16th 2014
- (edited Feb 16th 2014)
Thanks for the comment, that makes sense.
Somehow more attention in the literature is on (implicitly) Wirthmüller contexts for (holonomic) D-modules, e.g.
- Joseph Bernstein, around p. 18 of Algebraic theory of D-modules (BernsteinDModule.pdf:file, ps, dvi)
discussing stuff as listed here
- Pavel Etingof, Formalism of six functors on all (coherent) D-modules (pdf)
Has anyone seen a derived geometry version of this?
-
- CommentRowNumber39.
- CommentAuthorIngoBlechschmidt
- CommentTimeMay 5th 2015
- (edited May 5th 2015)
At quasicoherent sheaf, there is the nice description of as sheaves on (with the Zariski topology) satisfying the condition “”. I believe that this condition in fact already implies the sheaf condition. Therefore can also simply by expressed as the (2-categorical) limit ; thus is the right Kan extension of (sending to ) along the inclusion .
This is similar, but not identical, to the characterization as a right Kan extension along mentioned in the article.
I’ll think about this some more and add it to the article if nobody objects.
-
- CommentRowNumber40.
- CommentAuthorZhen Lin
- CommentTimeMay 5th 2015
It surely implies the sheaf condition – after all, every scheme has a cover by affine schemes, so the claim reduces to the theorem (which becomes a definition here…) that quasicoherent sheaves on affine schemes are the same as modules over rings.
-
- CommentRowNumber41.
- CommentAuthorIngoBlechschmidt
- CommentTimeMay 6th 2015
- (edited May 6th 2015)
Thanks for the confirmation! I don’t quite see how you reduce to affine schemes; my proof would go like this: Abusing notation and simply writing for , where is some fixed morphism, we have to verify that
where , is an equalizer diagram. By assumption, this diagram is isomorphic to
That this diagram is an equalizer diagram (even for any module ) is a basic fact of commutative algebra; for instance, it follows from the fact that is a sheaf on .
-
- CommentRowNumber42.
- CommentAuthorzskoda
- CommentTimeMay 6th 2015
- (edited May 6th 2015)
Sorry, misunderstood question.
-
- CommentRowNumber43.
- CommentAuthorZhen Lin
- CommentTimeMay 6th 2015
@Ingo
Yes, that’s what I meant. But I see that you meant to show that it is a sheaf on the gros Zariski site – I was thinking about the small Zariski site.
-
- CommentRowNumber44.
- CommentAuthorIngoBlechschmidt
- CommentTimeJan 16th 2017
- (edited Jan 16th 2017)
I added to quasicoherent sheaf a synthetic characterization of quasicoherence using the internal language of the big Zariski topos.
Briefly, a sheaf is quasicoherent if and only if the canonical map
is bijective for all finitely presented -algebras; this has a geometric interpretation outlined in the entry.
Also, for a quasicoherent -algebra , the canonical map
is bijective, which codifies the usual intuition that an element of an algebra should be viewed as a function on the spectrum of .
-
- CommentRowNumber45.
- CommentAuthorn.mertes
- CommentTimeMay 23rd 2020
Let be a ring (commutative with identity). Then the category of -modules is equivalent to the category of abelian group objects in the overcategory CommRings/. Switching to the algebro-geometric picture, this is the same as saying that the category of quasi-coherent sheaves on Spec is equivalent to the category of abelian cogroup objects in the undercategory Spec\AffSchemes.
Now let be a scheme. Is it true that the category of quasi-coherent sheaves on is equivalent to the category of abelian cogroup objects in the undercategory \Schemes?
-
- CommentRowNumber46.
- CommentAuthorDmitri Pavlov
- CommentTimeMay 23rd 2020
Re #45: It appears that both sides of your conjectural equivalence satisfy Zariski descent. So the claim follows from the affine case.
-
- CommentRowNumber47.
- CommentAuthorGuest
- CommentTimeJan 12th 2023
In the section "By maps into the stack QCoh" the functor QC should take values in ∞-groupoids, right? - Shane -
- CommentRowNumber48.
- CommentAuthorperezl.alonso
- CommentTimeApr 9th 2024
- (edited Apr 9th 2024)
In By maps into the stack QCoh, to compute the quasi-coherent sheaves of a stack, how is QC taken to be a functor valued in ooGrpd and not just (oo,1)Cat?
Edit: realised this duplicates the comment above. Judging by the discussion here, seems this is a typo and there’s nothing else really going on, so I changed it.
-
- CommentRowNumber49.
- CommentAuthorperezl.alonso
- CommentTimeApr 10th 2024
pointer to section
- Section 3 in. Luigi Alfonsi, Charles A. S. Young. Towards non-perturbative BV-theory via derived differential geometry (2023). (arXiv:2307.15106).
1 to 49 of 49