nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorAndrew Stacey
- CommentTimeJan 15th 2010
Started thinking about smooth paths.
(Incidentally, David, do you want query boxes added to your web? And would you like to change the CSS for off-web links from those boxes to some nice colour?)
-
- CommentRowNumber2.
- CommentAuthorDavidRoberts
- CommentTimeJan 16th 2010
Yes please. Edit the relevant pages as you see fit, and ask lots of questions! Also yes to the CSS change - the boxes are almost as bad as the little marching ants in a certain office suite. -
- CommentRowNumber3.
- CommentAuthorDavidRoberts
- CommentTimeJan 16th 2010
Replied to Andrew's question at which smooth paths do I use (davidroberts) -
- CommentRowNumber4.
- CommentAuthorAndrew Stacey
- CommentTimeJan 17th 2010
CSS changed. Feel free to ask if you want the colours tweaked.
-
- CommentRowNumber5.
- CommentAuthorAndrew Stacey
- CommentTimeJan 22nd 2010
The discussion rumbles on ... (in case anyone else is interested in following along)
-
- CommentRowNumber6.
- CommentAuthorAndrew Stacey
- CommentTimeJan 25th 2010
Sketched out the definition of the manifold structure on the space of 2-tracks in a manifold.
(Stuck it in the page which smooth paths do I use (davidroberts) as I wasn't sure if this was what David wants at the manifold of 2-arrows (davidroberts) so played safe.)
-
- CommentRowNumber7.
- CommentAuthorAndrew Stacey
- CommentTimeJan 28th 2010
Question for David:
Do the fibre categories of 2-tracks fit together into one big smooth manifold (over M), or are they separate?
So when building the space of 2-tracks in a manifold, we have the three layers:
2-tracks -> paths -> end-points
When building a neighbourhood of a 2-track, we want to allow the paths to vary a little. Do we also allow the end-points to vary?
Clearly, if we can do it with end-points varying then we can do it with them fixed. I think that it is possible to do it with them varying, but requires a little more work (I think it needs the fact that the loop fibration,
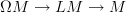 is a locally trivial fibre bundle, not just a fibration) and the construction will be just a little more opaque.
is a locally trivial fibre bundle, not just a fibration) and the construction will be just a little more opaque.Which do you want?
-
- CommentRowNumber8.
- CommentAuthorDavidRoberts
- CommentTimeJan 28th 2010
- (edited Jan 29th 2010)
(aarg - still can't get LaTeX to work here - bear with me)
Do the fibre categories of 2-tracks fit together into one big smooth manifold (over M), or are they separate?
They most definitely fit together into one manifold, else there would not be the map
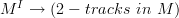 associating to a path the identity 2-track
associating to a path the identity 2-trackWhen building a neighbourhood of a 2-track, we want to allow the paths to vary a little. Do we also allow the end-points to vary?
We do want the endpoints to vary - if
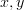 are points in
are points in 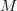 ,
, 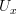 and
and 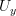 are charts (in
are charts (in 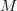 ) around them,
) around them, 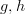 paths between them and
paths between them and 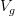 ,
, 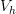 charts around them (in
charts around them (in 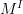 ) and
) and ![[f] [f]](/extensions/vLaTeX/cache/latex_c1213a45c943aa6068933848ff729220.png) a 2-track from
a 2-track from 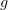 to
to 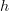 , then a chart around
, then a chart around ![[f] [f]](/extensions/vLaTeX/cache/latex_c1213a45c943aa6068933848ff729220.png) should look like
should look like 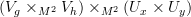 . (edit: It just occurred to me that this so-called chart could look crazy - not like our model TVS at all. Hmmm Is this where you need to use the local triviality of the loop fibration?)
. (edit: It just occurred to me that this so-called chart could look crazy - not like our model TVS at all. Hmmm Is this where you need to use the local triviality of the loop fibration?) -
- CommentRowNumber9.
- CommentAuthorDavidRoberts
- CommentTimeJan 28th 2010
Also, re your previous comment all the stuff on my web can go on one page, and be formatted/distributed later into a more user-friendly version
-
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeJan 29th 2010
- (edited Jan 29th 2010)
The trick with LateX here is
always include in double dollar signs (so a total of 4! :-)
no line breaks inside the dollar sings
Used to be difficult for me, as by default I usually put a line break after and before a double dollar sign.
-
- CommentRowNumber11.
- CommentAuthorTobyBartels
- CommentTimeJan 29th 2010
You just have to remember that the double dollar signs are really single dollar signs; there is no support for displayed equations as such. You just have to double them for the sake of the Forum's parser for some reason.
(I see that David has figured it out between my comment and Urs's above.)
-
- CommentRowNumber12.
- CommentAuthorAndrew Stacey
- CommentTimeJan 29th 2010
@David: Great! That's certainly the more interesting case, and it will use the locally trivial structure in a non-trivial way (though I'm not completely sure of the details). Imagine moving the end-point of (a path that's the end-point of ) a track a little bit: you want the whole track to move with you.
@Everyone else: yes, I suppose you're right. You should complain to the idiot who designed the LaTeX capability on this forum and demand your money back. Slightly more seriously, tips like those should go on the FAQ (linked from the menu on the bar at the top of these pages), if they aren't already there.
-
- CommentRowNumber13.
- CommentAuthorAndrew Stacey
- CommentTimeMar 8th 2010
Finally (gosh, over a month later!) written up the basics of the chart maps for 2-tracks with allowing endpoints to vary.
Annoyingly, the SVG-editor wasn't playing nicely with me so there's an unfinished diagram. I'll clean it up when I can get to a better browser.
-
- CommentRowNumber14.
- CommentAuthorDavidRoberts
- CommentTimeApr 15th 2010
Hi Andrew: here are some comments that you can look back over once you have time to pick up the project.
one thing which I would like to address is the putative equivalence between the topological Pi_2^top and the smooth Pi_2^sm. For a start we need the topology on the smooth Pi_2, in particular the space of 1-arrows which is the free (smooth) path space. This is, I gather from your comments in other places, not the same as the compact-open topology. I would like it if the map PM -> M^I is continuous where the former is the space of smooth paths (with topology coming from the manifold structure) and the latter is the space of continuous paths (with the compact-open topology).
Since all we need to show that a 2-functor between bigroupoids is an equivalence is the underlying truncated globular structure, we should be able to go from here to showing whether Pi_2^sm -> Pi_2^top' is an equivalence, where for the time being Pi_2^top' is Pi_2^top but with the concatenation of paths as in Pi_2^sm (i.e. using the bijective function [0,1] -> [0,2] flat at 1/2). My guess is that it is then quite easy to show that Pi_2^top' -> Pi_2^top is an equivalence: just need to construct it.
Then with the above result, we know that the source fibre of Pi_2^sm over a point is 2-connected (from bits in my thesis) and with a little work we should be able to show that the assignment M |-> source fibre(Pi_2^sm(M)) is functorial. This gives a functorial _smooth_ 2-connected 'cover' of a fin dim manifold, a genuinely new result. The next tricky bit is showing that this thing is a 2-covering space, but that is a little way off (or a long way, even!) -
- CommentRowNumber15.
- CommentAuthorAndrew Stacey
- CommentTimeApr 16th 2010
This is, I gather from your comments in other places, not the same as the compact-open topology.
Let me just comment on that quickly to clear it up. There’s a difference between paths on and paths on . With paths on , if one wants a manifold structure then one has to consider a slightly bizarre topology on . The easiest way to show how bizarre it is is to point out that it has uncountably many connected components: and are in the same component if outside some compact set. However, the conclusion of that is not that we use with a different topology, but that we say “Oh well, it’s not a manifold, it’s an X space.” (Frölicher, diffeological, what-have-you). With , though, there’s no difficulty because is compact and it is a manifold and it has the right topology. The problem is merely that “free path space” is ambiguous and can refer to both open or closed paths depending on context.
-
- CommentRowNumber16.
- CommentAuthorAndrew Stacey
- CommentTimeApr 16th 2010
I’ve also split off smooth fundamental bigroupoid (davidroberts) from the page which smooth paths do I use (davidroberts) to make it easier to focus on.
-
- CommentRowNumber17.
- CommentAuthorDavidRoberts
- CommentTimeApr 17th 2010
re #15 ok - we won’t look at open paths :)
And thanks for splitting the pages up.
-
- CommentRowNumber18.
- CommentAuthorAndrew Stacey
- CommentTimeJun 9th 2010
As I threatened to do elsewhere, I’ve extended the construction of the smooth fundamental bigroupoid to a suitable pair . Although I write , I don’t assume that Frolicher spaces have natural boundaries, this is a statement about pairs. I still have more checking to do on the details, and I guess I should expand on the transition maps. The conditions that the pair have to satisfy are:
- is a sequentially compact Frolicher space
- is closed in (so is again sequentially compact)
- is a deformation retract of a neighbourhood in , so there is a smooth function such that for , for all , and for all .
- There is a bump function on taking the value on and supported in .
I guess that 3 and 4 could be simplified slightly. If 3 is weakened to the existence of and a smooth map which is homotopic (rel ) to the identity on , then we can use the bump function from 4 to extend this to all of .
One advantage for me in this generalised approach is that it helps me separate out all the uses of the interval! When considering maps from then it’s hard to keep track of which is which.
The page in question is smooth+fundamental+bigroupoid (davidroberts)
1 to 18 of 18