Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology definitions deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory object of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: cohomology

Bottom of Page

1 to 13 of 13

  1.  
    • CommentRowNumber1.
    • CommentAuthorUrs
    • CommentTimeJan 21st 2010
    • (edited Jan 21st 2010)

    I further worked on the Idea-section at cohomology, expanding and polishing here and there.

    Hit "see changes" to see what I did, precisely: changes (additions, mostly) concern mainly the part on nonabelian cohomology, and then at the end the part about twisted and differential cohomology.

    by the way, what's your all opinion about that big inset by Jim Stasheff following the Idea section, ended by Toby's query box? I think we should remove this.

    This is really essentially something I once wrote on my private web. Jim added some sentences to the first paragraph. Possibly he even meant to add this to my private web and by accident put it on the main Lab. In any case, that part is not realy fitting well with the flow of the entry (which needs improvement in itself) and most of the information is repeated anyway. I am pretty sure Jim won't mind if we essentially remove this. We could keep a paragraph that amplifies the situation in Top a bit, in an Examples-section.

    What do you think?

    • CommentRowNumber2.
    • CommentAuthorMike Shulman
    • CommentTimeJan 21st 2010

    I think it could essentially be removed, but the part about connecting to classical notions is important and should be kept somewhere.

  3. maybe somewhere in the part on nonabelian cohomology one could add a line to say that characteristic classes of G-bundles are nothing but the composition . but cohomology already seems quite full of contents and I'm not sure about adding more stuff.
    • CommentRowNumber4.
    • CommentAuthorUrs
    • CommentTimeJan 22nd 2010

    good point. We need an entry on characteristic classes anyway. I'l start one now...

    • CommentRowNumber5.
    • CommentAuthorzskoda
    • CommentTimeJan 22nd 2010
    • (edited Jan 22nd 2010)

    I am leaving offline in a bit. So a tip for characteristic class. There is a noncommutative version fo Chern Weil theory in

    Victor Ginzburg, Lectures on noncommutative geometry, math.AG/0506603

    • CommentRowNumber6.
    • CommentAuthorUrs
    • CommentTimeJan 22nd 2010

    So a tip for characteristic class.

    Thanks, Zoran! I am reading...

    • CommentRowNumber7.
    • CommentAuthorUrs
    • CommentTimeJan 22nd 2010

    spent some time improving the general structure at cohomology. also started including a few more aspects, such as char classes. but they kicked me out of my guest office now, so i have to continue later

    • CommentRowNumber8.
    • CommentAuthorUrs
    • CommentTimeJan 24th 2010

    fixed the notation that Mike pointed out on the blog at

    and rephrased the entire paragraph a bit, I think it should flow better now.

    Also polished other things here and there and expanded the "section overview" at the end of the main part of the "Idea" section.

    • CommentRowNumber9.
    • CommentAuthorDavid_Corfield
    • CommentTimeJan 28th 2010
    "where the V are one-point compactifications of linear representation spaces of a group G."

    Did you mean the $S^V$ are one-point compactifications of linear representation spaces $V$ of a group G?
    • CommentRowNumber10.
    • CommentAuthorUrs
    • CommentTimeJan 28th 2010

    oh, yes, could you just quickly correct that for me, as I am in a rush. Thanks!

    • CommentRowNumber11.
    • CommentAuthorDavid_Corfield
    • CommentTimeJan 28th 2010
    Someone seems to have done it already.

    I wonder why you have the sense that exotic gradings could be reduced to ordinary ones. Do the ordinary ones arise for nonequivariant cohomology because of the representation theory of the trivial group?
    • CommentRowNumber12.
    • CommentAuthorUrs
    • CommentTimeJan 28th 2010

    Someone seems to have done it already.

    Was me after all. Five minutes later I needed to add an html anchor to the BiGrading section anyway, so I also fixed the 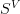S^Vs. Sorry. Or thanks. Or both! :-)

    I wonder why you have the sense that exotic gradings could be reduced to ordinary ones.I wonder why you have the sense that exotic gradings could be reduced to ordinary ones.

    One thing is that I would find it a pity if there were not a more systematic interpretation for an ad-hoc construction that has provne its value in practice. Usually such things have a deeper meaning, then.

    Secondly, my local equivariant guru keeps emphasizing to me that in most of the cases where one actually works with these beast, those linear representations of G on 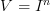V = I^n act just by permutations of the interval object facors I = \mathbb{R} .

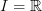    That makes it look to me like in a context where G-spectra are regarded as stabilized oo-stacks on the whole category of G-spaces, these exotic spheres are essentially just the spheres obtained from the line object 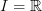I = \mathbb{R} regarded as a G-space with a trivial G-action.

    But I don't know.

    Currently I am reading the latest articles by Greenless where he discusses rational G-spectra. Turns out that these now are the same as "naive" rational G-spectra after all. Hence, stabilized oo-stacks over 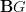\mathbf{B}G . (Not sure if that is useful for this question, though.)

    • CommentRowNumber13.
    • CommentAuthorMike Shulman
    • CommentTimeJan 30th 2010

    Well, I'm sure you know this, but having a "systematic interpretation" doesn't always mean "reducing it to a particular system we had in mind in advance." Sometimes it means "expanding the notion of system we had originally in mind to a more general system which includes more things that have value in practice."

1 to 13 of 13

  1.