nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeJan 23rd 2010
- (edited Jan 23rd 2010)
I am in the process of preparing a piece on Hochschild cohomology
while the Lab is down, I'll abuse the forum here for posting my source. Probably not well suited for reading it, but just so the effort is not wasted should my notebook get run over by a bus. That could happen, as the buses here in Sheffield go on the wrong side of the road.
See followup comment...
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeJan 23rd 2010
Contents
- automatic table of contents goes here {:toc}
Idea
Hochschild homology and cohomology are characteristic objects associated to a bimodule $N$ over an algebra object $A$.
If the algebra object in question plays the role of an algebra of functions on a geometric object, $A = C(X)$ then this has geometric interpretations. Notably
the Hochschild homology of $A$ regarded as a bimodule over itself tends to be like the algebra of Kähler differentials $\Omega^\bullet_K(A)$ on $A$, and hence something like the algebra of differential forms on $X$;
the Hochschild cohomology of $A$ regarded as a bimodule over itself tends to be like the algebra of derivations $Der(A)$ of $A$, and hence something like the vector fields on $X$.
The seminal Hochschild-Kostant-Rosenberg theorem states that under suitable conditions on $A$, these statements become exactly true.
Notice that differential forms are objects in de Rham cohomology but are still computed by the Hochschild homology of $A$. We should think of this as a result of the dualization in passing from the space $X$ to the algebra of functions $A = C(X)$ on it: it is the Hochschild homology of algebra objects that relates to the cohomology of spaces.
Below in section The nPOV on Hochschild cohomology we discuss a conceptual interpretation of Hochschild homology, that will explain why this is true, and what Hochschild homology is conceptually, from the nPOV on cohomology, as described there.
Complementary to that, in the section More traditional description of Hochschild cohomology we describe the original definition of Hochschild cohomology and the evolution of its understanding approaching the nPOV.
Finally in the section titled Details the technical details are spelled out.
More traditional descriptions of Hochschild cohomology
Originally the notion of Hochschild cohomology was introduced as the cochain cohomology] of a certain [[cochain complex associated to any bimodule $N$ over some algebra $A$: its bar complex, written

where $N$ and $A$ are regarded as $A \otimes A^{op}$-bimodules in the obvious way.
Then it was understood that this complex is the result of tensoring the $A$-bimodules $N$ with $A$ over $A \otimes A^{op}$ but using the derived functor of the tensor product functor -- the Tor functor -- in the ambient model structure on chain complexes:

Then still a little later, it was understood that this is just the ordinary tensor product in the symmetric monoidal (infinity,1)-category of chain complexes. If this is understood, we can just write again simply

This, generally, is the definition of the Hochschild cohomology object of any bimodule over an algebra object in a monoidal (infinity,1)-category. Of special interest is the case where $N = A$. In this case this object is also called the ("$(\infty,1)$-" or "derived-")center of $A$:

In parallel to this formal understanding of Hochschild cohomology, its conceptual meaning has been better understood: from staring at the explicit description of $C_\bullet(N,A)$ one sees that it has something to do with loop space objects: a chain in $C_n(N,A)$ is usefully thought of as a circle with $n$ marked points. One of these points is labeled $N$, the other are labeled $A$. The differential on $C_\bullet(N,A)$ acts by taking tensor products over $A$ separately of all neighbour pairs of bimodules sitting on this circle, and taking the alternating sum of this as a collection of such circles with $(n-1)$ marked points.
A fully geometric understanding of these was given by Ben-Zvi/Nadler/Francis in their work on geometric infinity-function theory. This we unify now with our nPOV perspective on cohomology in order to give the following nPOV perspective on Hochschild cohomolohy.
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeJan 23rd 2010
<h3 id="nPOV">The $n$POV on Hochschild cohomology</h3> <p>Let $\mathbf{H}$ be an <a href="https://ncatlab.org/nlab/show/%28infinity%2C1%29-topos">(infinity,1)-topos</a> of $(\infty,1)$-sheaves and $\mathbf{K}$ the $(\infty,2)$-topos of $(\infty,2)$-sheaves on a <a href="https://ncatlab.org/nlab/show/site">site</a> $C$, such that the <a href="https://ncatlab.org/nlab/show/quasicoherent+infinity-stack">quasicoherent infinity-stack</a></p> <p><img src="/extensions/vLaTeX/cache/latex_f2036c05b6589fe86fdbe2d38592c3c0.png" title=" C : C^{op} \to (\infty,1)Cat " style="vertical-align:-20%;" class="tex" alt=" C : C^{op} \to (\infty,1)Cat " /> <img src="/extensions/vLaTeX/cache/latex_d2fcd7962c545039a66700a7fbb20846.png" title=" U \maptso Stab(C_{/U}) " style="vertical-align:-20%;" class="tex" alt=" U \maptso Stab(C_{/U}) " /></p> <p>as described at <a href="https://ncatlab.org/schreiber/show/infinity-vector+bundle">infinity-vector bundle (schreiber)</a> does indeed satisfy <a href="https://ncatlab.org/nlab/show/descent">descent</a> in that it is indeed an object in $\mathbf{K}$.</p> <p>Recall that for $X \in \mathbf{H} \subset \mathbf{K}$ any object, its <a href="https://ncatlab.org/nlab/show/free+loop+space+object">free loop space object</a> $\mathcal{L} X$ is the $(\infty,1)$-<a href="https://ncatlab.org/nlab/show/pullback">pullback</a></p> <img src="/extensions/vLaTeX/cache/latex_427af5f342ecefa37675ab16a09e94b3.png" title=" \array{ && \mathcal{L} X \\ & \swarrow && \searrow \\ X &&&& X \\ & {}_{\mathllap{(Id,Id)}}\searrow && \swarrow_{\mathrlap{(Id,Id)}} \\ && X \times X } \,. " style="vertical-align:-20%;" class="tex" alt=" \array{ && \mathcal{L} X \\ & \swarrow && \searrow \\ X &&&& X \\ & {}_{\mathllap{(Id,Id)}}\searrow && \swarrow_{\mathrlap{(Id,Id)}} \\ && X \times X } \,. " /> <p>Notice that this is usefully thought of as the <a href="https://ncatlab.org/nlab/show/span+trace">span trace</a> of the <a href="https://ncatlab.org/nlab/show/identity">identity</a> <a href="https://ncatlab.org/nlab/show/span">span</a></p> <img src="/extensions/vLaTeX/cache/latex_3bcd26975d28218681310b2878524509.png" title=" \mathcal{L} X = Tr \left( \array{ && X \\ & {}^{\mathllap{Id}}\swarrow && \searrow^{\mathrlap{Id}} \\ X &&&& X } \right) \,. " style="vertical-align:-20%;" class="tex" alt=" \mathcal{L} X = Tr \left( \array{ && X \\ & {}^{\mathllap{Id}}\swarrow && \searrow^{\mathrlap{Id}} \\ X &&&& X } \right) \,. " /> <p>Assume that $X$ is such that on it $C$ satisfies the axioms of <a href="https://ncatlab.org/nlab/show/geometric+function+theory">geometric function theory</a> (see <a href="https://ncatlab.org/nlab/show/geometric+infinity-function+theory">geometric infinity-function theory</a> for more details).</p> <p>Then:</p> <p>The <strong>Hochschild cohomology of $X$</strong> is the <a href="https://ncatlab.org/nlab/show/cohomology">cohomology</a> of the <a href="https://ncatlab.org/nlab/show/free+loop+space+object">free loop space object</a> $\mathcal{L}X$ with coefficients in $C$:</p> <img src="/extensions/vLaTeX/cache/latex_e084e75065f26daca0dd258fe6e9e780.png" title=" HH(X) = \mathbf{K}(\mathcal{L}X, C) =: C(\mathcal{L}X) \,. " style="vertical-align:-20%;" class="tex" alt=" HH(X) = \mathbf{K}(\mathcal{L}X, C) =: C(\mathcal{L}X) \,. " /> <img src="/extensions/vLaTeX/cache/latex_56ce5cb34113d569c53dd409f29c8559.png" title=" HH^n(X) := HH_n(C(X)) := \pi_0\Omega^n\mathbf{H}(\mathcal{L}X, C) \,. " style="vertical-align:-20%;" class="tex" alt=" HH^n(X) := HH_n(C(X)) := \pi_0\Omega^n\mathbf{H}(\mathcal{L}X, C) \,. " /> <p>By the assumption that $C(-)$ is a <a href="https://ncatlab.org/nlab/show/geometric+function+theory">geometric function object</a> on $X$ we can rewrite</p> <img src="/extensions/vLaTeX/cache/latex_10cdb8c9eac6b946dde21d862d4e3101.png" title=" HH(X) = \mathbf{H}(\mathcal{L}X,C) =: C(\mathcal{K}X) " style="vertical-align:-20%;" class="tex" alt=" HH(X) = \mathbf{H}(\mathcal{L}X,C) =: C(\mathcal{K}X) " /> <p>as</p> <img src="/extensions/vLaTeX/cache/latex_4cfaa13b05f7aabd8c12521adf77706a.png" title=" \cdots \simeq C(X) \otimes_{C(X)\otimes C(X)^{op}} \infty Mod(X) \,. " style="vertical-align:-20%;" class="tex" alt=" \cdots \simeq C(X) \otimes_{C(X)\otimes C(X)^{op}} \infty Mod(X) \,. " /> <p>This is hence indeed the Hochschild homology object $HH_\bullet(A) = A \otimes_{A \otimes A^{op}}$ of the algebra object $A = \infty Mod(X)$, regarded as a bimodule over itself.</p> <p>More generally, let $f : Y \to X$ be a morphism in $\mathbf{H}$ and consider the <a href="https://ncatlab.org/nlab/show/span+trace">span trace</a></p> <img src="/extensions/vLaTeX/cache/latex_f9060f681e1a2e9027a7c4dafa4d01db.png" title=" \mathcal{L}_X Y := Tr \left( \array{ && Y \\ & {}^{\mathllap{f}}\swarrow && \searrow^{\mathrlap{f}} \\ X &&&& X } \right) " style="vertical-align:-20%;" class="tex" alt=" \mathcal{L}_X Y := Tr \left( \array{ && Y \\ & {}^{\mathllap{f}}\swarrow && \searrow^{\mathrlap{f}} \\ X &&&& X } \right) " /> <p>which is the $(\infty,1)$-pullback</p> <img src="/extensions/vLaTeX/cache/latex_8879d3315f39ac5d2b39c0931577545e.png" title=" \array{ && \mathcal{L}_X Y \\ & \swarrow && \searrow \\ Y &&&& X \\ & {}_{\mathllap{f,f}}\searrow && \swarrow_{\mathrlap{Id,Id}} \\ && X \times X } \,. " style="vertical-align:-20%;" class="tex" alt=" \array{ && \mathcal{L}_X Y \\ & \swarrow && \searrow \\ Y &&&& X \\ & {}_{\mathllap{f,f}}\searrow && \swarrow_{\mathrlap{Id,Id}} \\ && X \times X } \,. " /> <p>Then we take the Hochschild cohomology of $Y$ relative to $f : Y \to X$ to be</p> <img src="/extensions/vLaTeX/cache/latex_6ac139edb040b9f19f6334afd43b450e.png" title=" HH(Y,X) := \mathbf{K}(\mathcal{L}_X Y, C) =: \infty Mod(\mathcal{L}_X Y) \,. " style="vertical-align:-20%;" class="tex" alt=" HH(Y,X) := \mathbf{K}(\mathcal{L}_X Y, C) =: \infty Mod(\mathcal{L}_X Y) \,. " /> <p>In the case that $f$ is such that $C(-) = \mathbf{K}(-,C)$ satisfies <a href="https://ncatlab.org/nlab/show/geometric+function+theory">geometric function theory</a> on it, this is</p> <img src="/extensions/vLaTeX/cache/latex_742e4a19dab1d2118d2ea43f48ae338b.png" title=" \cdots = C( Y \times_{X \times X} Y) \simeq C(Y) \otimes_{C(X) \otimes C(X)^{op}} C(X) \,. " style="vertical-align:-20%;" class="tex" alt=" \cdots = C( Y \times_{X \times X} Y) \simeq C(Y) \otimes_{C(X) \otimes C(X)^{op}} C(X) \,. " /> <p>This is indeed the Hochschild homology object of the $C(X)$-bimodule object structure on $C(Y)$ induced from $f^*$:</p> <img src="/extensions/vLaTeX/cache/latex_61634fef6916a0bf5c5287ea380fcc6a.png" title=" \cdots =: HH_\bullet(C(Y), C(X)) \,. " style="vertical-align:-20%;" class="tex" alt=" \cdots =: HH_\bullet(C(Y), C(X)) \,. " /> <h2 id="Details">Details</h2> <p>...</p> <h3>The bar complex</h3> <blockquote> <p>The bar complex is called the bar complex because its inventors wrote it down using lots of bars. If you don't believe this it shows that you have no idea how careless mathematicians can be about finding good terminology for the objects they hold in high esteem.</p> </blockquote> <h2>References</h2> <p>The traditional story of Hochschild (co)homology is discussed for instance in chapter 4 of</p> <ul> <li><a href="https://ncatlab.org/nlab/show/Viktor+Ginzburg">Viktor Ginzburg</a>, <em>Lectures on noncommutative geometry</em> (<a href="">arXiv:math/0506603</a>)</li> </ul> <p>The $(\infty,1)$-categorical picture with its relation to <a href="https://ncatlab.org/nlab/show/geometric+infinity-function+theory">geometric infinity-function theory</a> is discussed in</p> <ul> <li><a href="https://ncatlab.org/nlab/show/David+Ben-Zvi">David Ben-Zvi</a>, <a href="https://ncatlab.org/nlab/show/David+Nadler">David Nadler</a>, <a href="https://ncatlab.org/nlab/show/John+Francis">John Francis</a>, <em><a href="https://ncatlab.org/nlab/show/geometric+infinity-function+theory">Integral transforms and Drinfeld centers in derived algebraic geometry</a></em> ([arXiv:0805.0157])</li> </ul> -
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeJan 23rd 2010
sorry for the above mess
something slightly more readable is beginning to appear now properly at Hochschild cohomology
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeJan 25th 2010
- (edited Jan 25th 2010)
I was reading again more in Ben-Zvi/Nadler "Loop spaces and Langlands parameters" and Toen/Vezzosi "S^1 equivariant simplicial algebras and de Rham theory".
This gives a beautiful geometric picture. It made me stay up and fiddle a bit more with the entry Hochschild cohomology. There is now for instance a slogan standout box right at the beginning, which I think describes the situation accurately. I think this is really nice.
The entry does not yet fully reflect all the details to support this general statement, though it does indicate all the central ingredients. If you are wondering, have a look at the above two article. Links are at the entry. It's all in there.
-
- CommentRowNumber6.
- CommentAuthorzskoda
- CommentTimeJan 25th 2010
You were really fruitful this weekend... :)
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeJan 25th 2010
Thanks, Zoran, I was hoping you would look into this and give me a sanity check, You and Mike are the ones to bring me back to earth when I get carried away with the nPOV, you especially for all things algebraic.
I think there is even more here than I have indicated, though. Ben-Zvi and Nadler in their article for instance discuss that the old idea that Kontsevich Pavol Severa and their school are so fond of: that NPQ-supermanifolds can be thought of as supermanifolds equipped with an action of the endomorphisms of the odd line, is really just yet another incarnation of derived loop spaces, the endomorphisms of the odd line being really the derived version of the
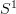 -action on the "derived loop"s.
-action on the "derived loop"s.Reading this (again) made me wonder (again) if not most of supergeometry is really best thought of as a simplified version of what really is derived geoemtry over formal duals of simplicial smooth rings.
-
- CommentRowNumber8.
- CommentAuthorzskoda
- CommentTimeJan 25th 2010
I hope you are right in this idea (that supergeometry is just a shadow of better'motivated general nonsense). I will continue try to contribute to your effort, though this week I can not neglect various deadlines any more as I did last 3-4 weeks.
Mamuka Jibladze was telling me in 2004 how there are very different models of loop spaces in connection to cyclic (co)homology and called some of them big and some of them small, even infinitesimal like in seminal work of Kapranov-Vasserot on chiral de Rham complex. It is worthy to look more into those.
-
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeJan 25th 2010
- (edited Jan 25th 2010)
Yes, In Ben-Zvi/Nadler they speak of the free loop space
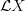 and of the Hochschild space
and of the Hochschild space 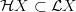 of infnitesimal loops inside that.
of infnitesimal loops inside that.For
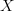 an ordinary (0-categorical) space both coincide. Which is remarkable enough: that a 0-categorical space, regarded as an object in a derived stack (oo,1)-topos, has any (categorical)loops at all and is hence no longer, in fact, 0-categorical.. This is a major deep aspect of the entire derived story. I tried to amplify this a bit at derived stack in the section on "derived Yoneda lemma".
an ordinary (0-categorical) space both coincide. Which is remarkable enough: that a 0-categorical space, regarded as an object in a derived stack (oo,1)-topos, has any (categorical)loops at all and is hence no longer, in fact, 0-categorical.. This is a major deep aspect of the entire derived story. I tried to amplify this a bit at derived stack in the section on "derived Yoneda lemma".Ben-Zvi/Nadler also mention cyclic models and also Kapranov-Vasserort.
There is, indeed, little on this planet that their article does not connect to ! ;-)
-
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeMar 23rd 2010
started a section in Hochschild cohomology on Classification of extensions
-
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeMar 23rd 2010
- (edited Mar 23rd 2010)
started a section on deformations at Hochschild cohomology
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeNov 24th 2010
I am further working on the section that demonstrates how the Hochschild complex of functions on is functions on the derived loop space of .
But I need to think about in which generality I can actually say this for general -algebras (for an algebraic theory). Maybe the proof currently displayed only makes sense for ordinary -algebras. Need to think about this. But now I need to run.
-
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeNov 24th 2010
I have polished a bit further. here is now a rather complete derivation of how the Hochschild complex is functions on the derived loop space.
I’ll now add the more traditional description in terms of derived tensor products of bimodules.
-
- CommentRowNumber14.
- CommentAuthorzskoda
- CommentTimeNov 24th 2010
One thing which I am uneasy about the entry is that it makes an impression that Hochschild cohomology is only HH(A,A), and not HH(A,M) with coefficient in an arbitrary bimodule M. The latter is the standard generality, while I understand that only the latter has a very special additional structures coming from the infinite-categorical interpretation. I think we should start with HH(A,M) first. I do not know if HH(A,M) can also be treated in more modern approach. -
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeNov 24th 2010
Right, I was thinking about that, too. But am unlikely to have time for it right now.
-
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeNov 24th 2010
- (edited Nov 24th 2010)
But I need to think about in which generality I can actually say this for general T-algebras
So I guess if I have a monad so that my algebra is a -algebra, then I can proceed entirely as in the section Hochscild complex on k-algebras as functions on derived loop space by
replacing the model structure on simplicial -algebras by the model structure on algebras over a monad on
replacing the bar complex by the corresponding monadic -bar construction
and otherwise proceeding essentially verbatim as before. That would give the -algebras of functions on derived loop spaces and a notion of Hochschild homology for general -algebras.
But I need to think more about the details…
-
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeNov 24th 2010
Hm, no, actually not quite. Because before I used not the monad for commutative -algebras, but that for modules over a fixed commutative -algebra.
Hm…
-
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeNov 24th 2010
- (edited Nov 24th 2010)
can somebody point me to good references on algebra structures on Hochschild chain complexes (for homology)? I have currently trouble finding the good reference that must exist out there…
-
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeNov 24th 2010
I think I found what I was looking for in
Dmitry Tamarkin and Boris Tsygan, Cyclic Formality and Index Theorems (journal)
and their reference 13.
But I’d still be grateful for further pointrs.
-
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeNov 24th 2010
added in the last section the little computation that shows that
-
- CommentRowNumber21.
- CommentAuthorUrs
- CommentTimeNov 24th 2010
Now there is even a section with the elementary definition.
-
- CommentRowNumber22.
- CommentAuthorUrs
- CommentTimeNov 24th 2010
it just occurs to me that we should have a much simpler and much more general statement:
one can see that for constant the internal hom in the -topos coincides with the powering over . In the situation over a site of formal duals of simplicial algebras, this translates simply into the copowering .
But for a simplicial set and an algebra, the simplicial algebra is precisely (under Dold-Kan) Pirashvilli’s definition of the Hochschild chain complex for any simplicial set.
I’ll write that out in detail in a moment. Need to make a telephone call first.
-
- CommentRowNumber23.
- CommentAuthorzskoda
- CommentTimeNov 24th 2010
Sounds very nice. Please make it easy to understand how this works. -
- CommentRowNumber24.
- CommentAuthorUrs
- CommentTimeNov 25th 2010
- (edited Nov 25th 2010)
okay, i restructured the Definition-section at Hochschild cohomology and gave the details for the statement mentioned in #22 above.
With the results about the internal hom in an -topos (now discussed at (infinity,1)-topos) the argument is actually quite simple: we get almost tautologuically that
at the -category level, where on the right we have the -tensoring of -algebras over -groupoids, So generally for every -groupoid define the higher order Hochschild complex to be .
Now, to get from there to Pirashvili’s slick definition of (higher order) Hochschild homology we just need to observe three things:
the formula for pairing a simplicial set with an algebra to a simplicial algebra that Pirashvili and everyone following him writes down is really nothing but the (ordinary 1-categorical) tensoring of the algebra with the simplicial set in the category of simplicial algebras
if the -algebras etc. are presented by a simplicial model category of simplicial algebras, then the -tensoring is presented by the ordinary tensoring in the model category;
and finally: there is a standard simplicial model structure for ordinary simplicial commutative associative -algebras (Goerss-Schemmerhorn).
That’s it. That gives us that the very-general-abstract definition “cohomology of the higher order loop space object ” is modeled by Pirashvili’s construction, if we are doing derived geometr over duals of ordinary commutative algebras.
And for derived geometry over general -algebras we can always use the model structure on homotopy T-algebras. That’s tivially a simplcial model category.
-
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeNov 25th 2010
so for any -groupoid and any -algebra, the higher order Hochschild homology is the tensoring . Notice that this is the -colimit over the diagram of the functor constant on
Now compare this to the definition of topological chiral homology on page 90, 91 in Classification of TFTs . You see it’s the same type of definition, of course. See example 4.1.22.
Will add that to the entry on Hochschild now.
-
- CommentRowNumber26.
- CommentAuthorUrs
- CommentTimeNov 25th 2010
- (edited Nov 25th 2010)
am starting a section Algebra structure on with references to differential calculus and BV-algebra structure.
-
- CommentRowNumber27.
- CommentAuthorUrs
- CommentTimeNov 25th 2010
Jones’ theorem relating Hochschild homology of singular cochains on a topological space to the singular cohomology of its loop space is now a direct consequence of the general abstract theory. I now wrote out the proof in the section of constant -stacks
-
- CommentRowNumber28.
- CommentAuthorUrs
- CommentTimeNov 25th 2010
added the proof of the Deligne-Kontsevich conjecture for the case of HH with coefficients in “geometric function objects” at -algeba structure on : Deligne-Kontsevich conjecture/theorem
-
- CommentRowNumber29.
- CommentAuthorUrs
- CommentTimeNov 25th 2010
- (edited Nov 25th 2010)
just found this article
Ginot, Tradler, Zeinalian, Derived higher Hichschild homology, topological chiral homology and factorization algebras pdf
which discusses these connections explicity.
In theorem, 4.2.2 they give an axiomatic characterization of the pairing . One can see that this is indeed the copowering of dgca over .
-
- CommentRowNumber30.
- CommentAuthorUrs
- CommentTimeNov 25th 2010
you know, if you look at all this now, what’s happening here is really this: the POV simplifies Hochschild homology to the extent that it disappears . There is no extra concept “Hochschild homology”. When formulated in sufficient generality one finds that one is just talking about the canonical powering of any -topos over .
-
- CommentRowNumber31.
- CommentAuthorMike Shulman
- CommentTimeNov 26th 2010
In the same way that the nPOV simplifies “cohomology” by making it disappear into the notion of “hom-space in an (∞,1)-category/topos”?
-
- CommentRowNumber32.
- CommentAuthorUrs
- CommentTimeNov 26th 2010
Yes, exactly!
-
- CommentRowNumber33.
- CommentAuthorUrs
- CommentTimeNov 26th 2010
- (edited Nov 26th 2010)
Look at that article by Grégory et al (end of the abstract is sufficient for what I say now), you see they show essentially that, slight reformulation in my words, the -powering operation over -groupoids gives the locally constant factorization algebras.
So there is an obvious thing to be said: since the powering in an -topos is the internal hom out of a constant -stack, eventually you want to pass to general internal homs out of non-constant -stacks. In view of the above, there is a natural guess for what that would give…
-
- CommentRowNumber34.
- CommentAuthorMike Shulman
- CommentTimeNov 26th 2010
So what does the nPOV make ordinary homology disappear into?
-
- CommentRowNumber35.
- CommentAuthorDavid_Corfield
- CommentTimeNov 26th 2010
-
- CommentRowNumber36.
- CommentAuthorDavid_Corfield
- CommentTimeNov 26th 2010
…and here.
-
- CommentRowNumber37.
- CommentAuthorUrs
- CommentTimeNov 26th 2010
- (edited Nov 26th 2010)
Right, so up to now I keep thinking that general homology is not as basic as cohomology or (as we see now) Hochschild homology: it does not in a similar manner boil down to being nothing but a very basic operation in higher category theory.
Rather, it seems to involve a bit of exatra structure and properties around. Such as: if we start with the very-general-abstract notion of cohomology and then specialize it to certain sufficiently abelian context, then there appears a dual theory, and that is homology.
Stated differently: the nice duality between homology and cohomology that one sees – tensor dual to hom, Tor dual to Ext – is nice and pretty, but does need a sufficiently abelian context. It does not make sense in the nonabelian general sense in which cohomology and Hochschild homology make sense in any -topos.
Or so it seems to me. I might be wrong. Also, probably even so, there should be a very basic nice formulation not in -toposes but maybe in stable -categories that makes homology “disappear into a basic category theoretic construction”.
-
- CommentRowNumber38.
- CommentAuthorTim_Porter
- CommentTimeNov 26th 2010
There are geometric treatments of homology (as I remember) that were based on using bordisms, etc. so is perhaps that approach worth looking into. (I have just crawled under my desk to get my copy of ‘ A geometric Approach to Homology Theory’ by Buoncristiano, Rourke and Sanderson, (1976), which states’ The purpose of these notes is to give a geometrical treatment of generalised homology and cohomology theories.’ Looking at the summary, there are points that may be useful. They claim that the basic idea is from Sullivan.
-
- CommentRowNumber39.
- CommentAuthorUrs
- CommentTimeNov 26th 2010
The purpose of these notes is to give a geometrical treatment of generalised homology and cohomology theories.
Just for emphasis: smashing with a spectrum and callling this a generalized homology is already very nice and abstract. The question is if one can understand it as something even more basic and abstract. Not sure.
-
- CommentRowNumber40.
- CommentAuthorUrs
- CommentTimeNov 26th 2010
- (edited Nov 26th 2010)
It would maybe make sense to say: homology is the tensoring operation in any -category that is tensored over the -category of spectra.
-
- CommentRowNumber41.
- CommentAuthorMike Shulman
- CommentTimeNov 28th 2010
Thanks for the links, David!
homology is the tensoring operation in any ∞-category that is tensored over the ∞-category of spectra
And it can be extended to a larger class of ∞-categories via mapping into their “stabilizations” which will then be tensored over spectra? I guess this uses the identification of A-valued homology groups of X with the homotopy groups of , where is the Eilenberg-Mac Lane spectrum that can be generalized to any other spectrum.
On the other hand, integral homology groups can also be identified with homotopy groups of the infinite symmetric product, i.e. the free topological abelian monoid. Does that construction have an ∞-categorical version?
-
- CommentRowNumber42.
- CommentAuthorUrs
- CommentTimeNov 29th 2010
- (edited Nov 29th 2010)
I guess this uses the identification of A-valued homology groups of X with the homotopy groups of , where is the Eilenberg-Mac Lane spectrum that can be generalized to any other spectrum.
That’s what I was thinking of, yes. So this gives the “chain complex” for homology, an object whose homotopy type or more strictly whose homotopy groups give the homology groups, proper. This should go with some extra discussion of homotopy groups of objects in stable -categories, I suppose.
On the other hand, integral homology groups can also be identified with homotopy groups of the infinite symmetric product, i.e. the free topological abelian monoid. Does that construction have an ∞-categorical version?
Not sure. Need to think about this.
-
- CommentRowNumber43.
- CommentAuthorUrs
- CommentTimeNov 29th 2010
- (edited Nov 29th 2010)
Just for the record: the expression of the Hochschild homology complex via categorical copowering is explicit in Toën-Vezzosi’s Algébres simpliciales S1-équivariantes et théorie de de Rham
-
- CommentRowNumber44.
- CommentAuthorUrs
- CommentTimeNov 30th 2010
- (edited Nov 30th 2010)
I wrote a section discussion just the simplicial algebra of functions on the circle, how it is the same as functions on the odd line and how this makes every Hochschild complex be equipped with its differential on its homology (the circle action in its homological incarnation).
The simplicial circle algebra.
My intention was to give a detailed component-wise discussion of how the quotient of by the simplicial circle action is manifestly the complex for cyclic homology (as it must be), but I still don’t see it in full detail. It must be quite simple, though.
I would have thought this is very explicitly in Toen-Vezzosi, but there construction is in fact quite far from being explicit. And, yes, i am well aware of what Ben-Zvi/Nadler write, but that, too, I want to spell out more explicitly, eventually.
But now I have to run to our TMF seminar.
-
- CommentRowNumber45.
- CommentAuthorUrs
- CommentTimeDec 2nd 2010
Maybe I did it myself and forgot, but I think sombody else added the following line to the references at Hochschild cohomology:
An original reference is
- Boris Tsygan, Feigin, Additive K-theory 1980-s (LNM 1289, editor Manin, pp 67-209, seminar 1984-1986 in Moscow)
What is it that this article says about Hochschild? If somebody has a quick answer, I’d be grateful. Otherwise I’ll try to look at it myself later.
-
- CommentRowNumber46.
- CommentAuthorzskoda
- CommentTimeDec 2nd 2010
- (edited Dec 2nd 2010)
It must be that somebody moved things around. Because this reference is one of the original references for cyclic homology, aka additive K theory. Of course it is related to the deeper study of Hochschild and topological Hochschild but this is an older subject. Feigin is also Boris. The reference is very comprehensive. It is difficult to say what is there and what is not. See MR89a:18017
-
- CommentRowNumber47.
- CommentAuthorzskoda
- CommentTimeDec 2nd 2010
- (edited Dec 2nd 2010)
More complete reference is
- Boris Tsygan, Boris Feigin, Additive K-theory, in LNM 1289 (1987), edited by Yu. I. Manin, pp. 67--209, seminar 1984-1986 in Moscow), MR89a:18017
I created entry additive K-theory with redirect Additive K-theory to explain both the term and to have few words about the reference.
-
- CommentRowNumber48.
- CommentAuthorUrs
- CommentTimeDec 2nd 2010
Thanks. And thanks for the article itself. I removed the reference at Hochschild and put it into cyclic cohomology
-
- CommentRowNumber49.
- CommentAuthorUrs
- CommentTimeDec 2nd 2010
Above I suggested that the explicit construction of higher order Hochschild complexes in Ginot-Tradler-Zeinalian’s recent article is secretly a model for the -copowering of dgc-algebras over -groupoids.
I am now writing out the detailed proof of this at The copowering of dgc-algebras over Grpd.
Currently I have a disclaimer there saying that this proof is still under construction, but I think I only need to provide and handful of links to statements that the model structure on dgc-alg meets the assumptions made.
-
- CommentRowNumber50.
- CommentAuthorzskoda
- CommentTimeDec 2nd 2010
Urs, there is a gap between the algebraic community doing Hochschild etc. for algebras and the -category parlance a la Lurie. Now when you are systematizing the relation between the two points I would dare an advice of awareness. In 1980-s and 1990-s there has been lots of work on Hochschild and cyclic (co)homologies for differential graded algebras and more recently in A-infinity algebra and dg- and A-infinity category setup (e.g. the Tsygan, Feigin article we just mentined also do Hochschild and cyclic right from the start in dg-setup). This is more or less close to infinity-categorical context, while the connection to the algebraic case is more directly seen.
-
- CommentRowNumber51.
- CommentAuthorUrs
- CommentTimeDec 2nd 2010
The relation between the two schools is the main point of Ben-Zvi/Nadler’s work. I am just trying to fill in some details. (Well, I find i have to fill in quite a few details, but probably that’s just me being dense…)
-
- CommentRowNumber52.
- CommentAuthorUrs
- CommentTimeDec 2nd 2010
By the way, Ginot et al are also making the connection to chiral homology, hence to something coming from the -category side of life.
-
- CommentRowNumber53.
- CommentAuthorUrs
- CommentTimeDec 7th 2010
I added a section Gradings and conventions in an attempt to make very clear how the unbounded cochain complexes here run, with the categorical degrees contributing positively, and the “derived” degress negatively.
-
- CommentRowNumber54.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 7th 2010
- (edited Dec 7th 2010)
I was looking at the proof of Deligne-Kontsevich conjecture as it is sketched at Hochschild cohomology. That suggests an immediate generalization to cobordism and tqft: for a fixed object , let us consider with a -dimensional manifold.
-
- CommentRowNumber55.
- CommentAuthorUrs
- CommentTimeDec 8th 2010
Yes, that’s what is called “higher order Hochschild cohomology”.
By the way, I am still working on this entry. I find I need to do quite a bit o work to fill in details of some of the statements about derived geometry in the literature.
In any case, I want to get away from using the model structure on commutative dg-algebras over a field of char=0. That this exists at all is kind of a coincidence or at least exceptional (it doesn’t in other characteristic) and lots of standard constructions fail because they don’t land in strictly commutative but in chain algebras.
So eventually I want to refine the whole discussion that is currently starting to appear in the section on dg-algebras to something better. But I still need to do some work on this.
-
- CommentRowNumber56.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 8th 2010
Hi Urs
I don’t like the name “higher order Hochschild cohomology” too much. I see it has been used in literature, but since it is a quite new term I think we could also not use it we don’t find it a good name, and acknowledge it as “this is sometimes called higher order Hochschild cohomology in literature, e.g., in…”. Here is my reason for disliking the term: “the higher order Hochshild cohomology of given by with coefficients in ” is just an absolutely not enlighting synonym for the clear “the cohomology of with coefficients in ”, and moreover distract attention from what is the crucial construction here, i.e., that if is an object in an (oo,1)-topos , then it is meaningful to consider the “space of maps from a topological space to ” and this is an object of .
Note how the situation is different for ordinary Hochshild cohomology: there the name “Hochshild” is specifying the oo-groupoid , so it is perfectly fine to say “Hochshild cohomology” a synonym of “cohomology of the loop space” .
So I strongly agree we should focus on the general construction of , or even better of , and as an happy byproduct recover known algebraic costructions.
Think to what happens for algebras. The classical algebraic version deals with an action of chains over the -little disks operad acting on a chain complex. And one takes chains over the topological operad in order to have something that can meaningfully act on chain complexes. But in the (oo,1)-perspective this is only a shadow of the fact that directly the little disk operad is acting, and in a more natural way. The same for -actions.
You obviously know this very well, I’m only saying it to stress my agreement on this point of view.
-
- CommentRowNumber57.
- CommentAuthorUrs
- CommentTimeDec 8th 2010
You are certainly right Domenico. I am not much attached to the term “higher order Hochschild homology” because, as you say, it makes a smple idea look intransparent.
But we need to keep at least some mention of it, before the rest of the wolrd is all on our side.
Also in the interest of better understandibility I have now edited the Intro of the entry, trying to make clearer the switch between cohomology of and homology of .
-
- CommentRowNumber58.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 8th 2010
- (edited Dec 8th 2010)
fine. also we should stress the natural action of on , in particular in the case. this is already stated clearly, and spelled out in detail; yet, calling it -action is actually a bit confusing, since the fact that (the connected component of identity of) is equivalent to is purely accidental, so the name -action distracts frome the true nature of what one is considering there and obscures the natural generalization to the case of ana arbitary .
(I must also say that I’m actually capable of no better name than -action, though)
the other point which came to my mind is that a few very vague thoughts we had some time ago about full extended tqft could now be expressed considering “functions on the internal oo-fundamental groupoid” of , i.e., .
-
- CommentRowNumber59.
- CommentAuthorUrs
- CommentTimeDec 8th 2010
Hi,
yes, i agree, more discussion of the -action is needed and instead of a circle action one should speak of an -action. Though it is specifically the circle action inside there that gives the de Rham differential.
This is related to the part that I am currently trying to spell out in more detail: I am still absorbed with writing out the full proof that .
This is clear when working in -stacks on duals of ordinary algebras, by use of the explicit Quillen adjunction descrived at function algebras on infinity-stacks. But it seems to me that lifting this statement to the derived context modeled on commutative dg-algebras requires a tad more discussion than is present in the literature. Maybe I am wrong.
Concerning QFT: what we should think about is how to fit in the -Chern-Simons theory: for an -Chern-Simons Lagrangian the -algebra assigned to a ought to be the sections of an associated bundle to the -bundle classified by the result of homming into the action functional – and possibly truncating. We have discussed several ways in which one can formalize this. But I am not sure yet exacty what the way to go is.
-
- CommentRowNumber60.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 8th 2010
- (edited Dec 8th 2010)
Though it is specifically the circle action inside there that gives the de Rham differential
yes. but this is just restriction to the connected component of the identity. what I’d like to stress is that the fact that is homotopy equivalent to the group of rotations of should be considered as an accidental equivalence.
Concerning tqft, the internal hom point of view suggests that we should think of , where is induced by the cocycle: and is induced by the morphism to the point: .
-
- CommentRowNumber61.
- CommentAuthorUrs
- CommentTimeDec 8th 2010
- (edited Dec 8th 2010)
should be considered as an accidental equivalence.
Yes, true.
Concerning tqft, the internal hom point of view suggests that we should think
Could you say why you think so? Let’s compare to the case that is replaced by a pseudo-Riemannian manifold and the action functional is a cocycle . Then to should be assigned something like the space of sections of the line bundle associated with this.
-
- CommentRowNumber62.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 8th 2010
this is precisely what I had in mind (but I could have expressed it wrongly): we start with the tautological line bundle on , we pull it back to a line bundle on and then we push this forward to a vector bundle over the point. this is the space of sections of the line bundle on associated with the cocycle . so my guess (or, maybe better, my hope) was that this could be written as .
-
- CommentRowNumber63.
- CommentAuthorUrs
- CommentTimeDec 8th 2010
- (edited Dec 8th 2010)
Okay, I see. The question is how to – in this sense – interpret in . It can’t be just plain -functions, as these are sections of a trivial bundle.
But there is a good way to speak about sections of associated bundles just in terms of ordinary functions, and maybe we need the -version of that. You know the following, but I say it anyway, for the record:
for an ordinary -principal bundle, sections of the associated line bundle over are identified with -invariant plain functions on :
This is the description of sections in terms of local trivializations over a cover in disguise: we may take as the cover and canonically trivialize over that by the principality isomorphism for .
Because on any cover on which trivializes, a section of the associated compex line bundle over is given by a function that satisfies the evident cocycle condition on double overlaps. For and using this is just the -equivariance of the function.
So given we might form the corresponding -bundle over the space of fields and then form .
-
- CommentRowNumber64.
- CommentAuthorUrs
- CommentTimeDec 8th 2010
- (edited Dec 8th 2010)
Hey, wait, what I just said may just prove your point:
The universal -principal bundle on is the point . I just argued that sections of the asociated line -bundle is -equuivariant -functions on that. But this is
edit: hm, something is strange, I need to think
-
- CommentRowNumber65.
- CommentAuthorUrs
- CommentTimeDec 8th 2010
- (edited Dec 8th 2010)
Let’s go more general abstract. We are talking about defining a structure based on an action functional given by a morphism. So we ought to be working in the corresponding over-topos.
So I guess we start with in and then first send it into where it becomes . By I mean a derived -site analog of , something like formal duals over simplical -rings whose is functions on a Cartesian space. Not yet sure about the details.
Let’s then think of this as an object in the over-(infinity,1)-topos . Every manifold of dim embeds into that as . So then we just ought to look at the higher order Hochschild cohomologhy of the -Chern-simons Lagrangian regarded as an object in this derived over -topos.
What does that give?
-
- CommentRowNumber66.
- CommentAuthorUrs
- CommentTimeDec 8th 2010
I wrote:
By I mean a derived (∞,1)-site analog of , something like formal duals over simplical -rings whose is functions on a Cartesian space. Not yet sure about the details.
That ought to be the evident slight variation of the definition at etale (infinity,1)-site.
In fact I think I can now give the -cohesive -site for the derived Cahier topos.
-
- CommentRowNumber67.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 8th 2010
- (edited Dec 8th 2010)
Hi Urs,
let us make a step back to concrete, i.e., to #64. The basic instance of what is discussed there is: What is ? I’m trying to work it out from the general definition given at Isbell duality, but I got lost :(
my idea is that the enrichment should be in simplicial vector spaces, but I may be completely out of track, here
-
- CommentRowNumber68.
- CommentAuthorUrs
- CommentTimeDec 8th 2010
What is
There are different contexts to interpret these symbols with different answers. If we read in the sense described at functional algebras on infinity-stacks and if we allow ourselves to work in the underived -topos for the moment, then this is the cosimplicial algebra of functions that is in degree the functions on the degree -presheaf of a cofibrant simplicial presheaf representing .
In fact I think we mainly need , where . For this a cofibrant simplicial presheaf (on the site ) is just the simplicial presheaf constant on the nerve of the one-object groupoid of with discrete smooth structure.
So that’s the cosimplicial algebra
After applying monoidal Dold-Kan correspondence or rather the discussion at cochain on a simplicial set this is incarnated as a dg-algebra whose cochain cohomology is .
But I am not necessarily claiming that this is what we need. For doing Hochschild homology we need to implement this computation over the -site of formal duals of simplicial -rings subject to sime conditions. The result of the above computation however ought to be unaffected by that, but I still don’t have a really good full hand-waving-free derivation of that. (I mentioned before that I am still struggling with this. Though it’s supposed to be obvious.)
But maybe, maybe, for our purposes we need to use an entirely different geometric infinity-function theory. Not but , for instance (see the link). This we need to figure out.
-
- CommentRowNumber69.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 9th 2010
In the meanwhile I’ve ben thinking of the integration/truncation issue. We have now it for external homs: , while we’d like a version for internal homs : .
At least for and we have this: . This is worked out in detail at free loop space object.
It therefore seems the case would be completely understood as soon as we bring into the game also the internal path space of along the lines discussed at interval object.
-
- CommentRowNumber70.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 9th 2010
the internal path space seems to be already described at free loop space object, in the detailed discussion on . In particular we have .
-
- CommentRowNumber71.
- CommentAuthorUrs
- CommentTimeDec 9th 2010
Yes, and that is equivalent to just , reflecting the fact hat .
-
- CommentRowNumber72.
- CommentAuthorUrs
- CommentTimeDec 10th 2010
- (edited Dec 10th 2010)
With the theorems meanwhile added to model structure on dg-algebras (for the unbounded commutative case) I have now finally filled the remaining gaps for the section on dg-geometry at Hochschild cohomology.
I have restructured that subsection HH modeled over cdg-algebras now. Notably there is now full proof in the subsection The circle and the odd line.
-
- CommentRowNumber73.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 10th 2010
Hi Urs,
concerning #71, of course it is, precisely because of the equivalence between and . this has been puzzling me for a while, yesterday, since I was unable to make the -version of fit the 1-dimensional cobordism framework. but then it is precisely as you say: they are just different ralizations of the same (up to equivalence, which is the only thing that matters) object.
the double quotient picture is the one suitable for directly interpreting a cocycle into as an isomorphism of principla -bundles (it is an precise incarnation of the classical picture that a morphism of principal -bundles is described locally by an element of the gauge group acting on frames, well defined up to local changes of gauge (i.e., changes of the local trivializations of the principal bundles)
the -version tells us that a cocycle into defines a princiapl -bundle (well defined up to isomorphism).
so I think it is important to have both pictures in mind: in the appliation to full extended tqft, one model will make us able to do explicit computations, but the fact that what we are dealing with is nothing but a model of an intrinsically defined object is what will give the independence of the result by the particular model chosen for the computation.
e.g., if we are able to make this work for with , then we are saying that “triangulation based” computations in the DW-model are actually triangulation independent (as they indeed are).
-
- CommentRowNumber74.
- CommentAuthorUrs
- CommentTimeDec 10th 2010
Yes, right, Even if equivalent, these “puffed-up” objects are important for gluing things together, yes.
-
- CommentRowNumber75.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 10th 2010
on second thought, I don’t think the right object to be considered is but rather its version relative to the boundary of . More in general, what is ? my guess is it should roughtly be the collection of homotopy fibers of , i.e., we that are dealing with (an internal version of) twisted cohomology.
just for the record, note by the way that when the coefficien object is pointed, doing this for the external homs rather than for the internal ones, i.e. defining the cohomology of a a pair as the homotopy fiber of over the distinguished point of , gives the long exact sequence of a pair in classical cohomology.
-
- CommentRowNumber76.
- CommentAuthorUrs
- CommentTimeDec 10th 2010
on second thought, I don’t think the right object to be considered is but rather its version relative to the boundary of . More in general, what is ? my guess is it should roughtly be the collection of homotopy fibers of , i.e., we that are dealing with (an internal version of) twisted cohomology.
that sounds right, yes
-
- CommentRowNumber77.
- CommentAuthorUrs
- CommentTimeDec 10th 2010
- (edited Dec 10th 2010)
I need to come back to something else:
I am currently struggling with understanding what is meant around page 10 of Ginot, Tradler, Zeinalian, when the commutative algebra structure on the higher order Hochschild chain complex is described.
First I thought a more detailed anwer is in the previous reference GTZ that is being pointed to in the proof of prop. 3.1.5, but it turns out that the text here is pretty much verbatim a copy of the text there. So it seems the content of page 10 is all we have and are supposed to need.
But I am not sure I am following. What I see described on page 10 is the commutative algebra structure on the chain complex of a simplicial algebra, essentially (it is not put in these words there) by using the fact that the Moore complex functor is symmetric lax monoidal via the Eilenberg-Zilber map.
But it seems to me the issue to be discussed is what to do if we now have a simplicial cdg-algebra . On that page 10 it keeps saying “simplicial vector space”. But it does not become clear (to me) what simplicial vector space exactly is meant.
Here is what I would think is meant:
the Dold-Kan correspondence works in any abelian category. And is an abelian category. So given a simplicial set and a cdg-algebra , we can form the simplicial cdg-algebra . Which in degree is the cdg-algebra , where the tensor product is that of cdgas.
Under the Moore complex functor this becomes a cochain complex in non-negative degree in cdgAlg, denoted . This is in total a double complex in . But let’s keep thinking of it as a chain complex in . Then by the fact that the Moore complex functor is symmetric lax monoidal (using the Eilenberg-Zilber shuffle map), we find that this is a commutative cochain dg-algebra in non-negative degree internal to .
It almost seems to me that what is meant on that page 10 is this situation, after applying the forgetful functor from to the underlyiing total vector spaces.
But to get from our dg-algebra internal to dg-algebras to a single dg-algebra, we still need to apply the total complex functor. That ought to preserve the algebra structures and thus finally produce a cdg-algebra structure on the higher order HH chain complex for us.
I guess.
-
- CommentRowNumber78.
- CommentAuthorUrs
- CommentTimeDec 10th 2010
We need that the total complex functor is symmetric lax monoidal, I suppose.
-
- CommentRowNumber79.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 11th 2010
Hi Urs,
what you say in #77 is a good idea: there’s already a lot to be said and cleaned about Hochschild cohomology (not to talk of higher order Hochschild cohomology) and we should not dissipate energies in too many directions. In the meanwhile I feel now I’m finally ready to really go through Topological Quantum Field Theories from Compact Lie Groups, so I’ll concentrate on that (cobordism is quite obsessing me, lately), posting a daily diary of my reading on the nforum (in another thread). Eventual clear mathematical statements will be pasted into the relevant nLab entries.
-
- CommentRowNumber80.
- CommentAuthorUrs
- CommentTimeMar 14th 2011
In reaction to David Ben-Zvi’s comment on the Cafe I have rewritten the Idea-section at Hochschild cohomology. While in the formal part of the entry the “-perfectness”-condition was stated clearly, the Idea-section took that for granted and thus probably gave a wrong general impression.
I hope it is better now.
-
- CommentRowNumber81.
- CommentAuthorMike Shulman
- CommentTimeAug 11th 2011
Is there anything on the nLab about Hochschild (co)homology for noncommutative algebras?
-
- CommentRowNumber82.
- CommentAuthorUrs
- CommentTimeAug 12th 2011
Is there anything on the nLab about Hochschild (co)homology for noncommutative algebras?
No, not yet.
-
- CommentRowNumber83.
- CommentAuthorzskoda
- CommentTimeAug 12th 2011
- (edited Aug 12th 2011)
Eventually I will try to balance it. The original idea was the noncommutative case, and much of the stuff on commutative case on this page does not hold in general. For commutative case, algebraists like Harrison cohomology. There are also the classic works for relations between Hochschild, Shukla and MacLane cohomology, it woudl be nice to treat the similarities and distinctions.
-
- CommentRowNumber84.
- CommentAuthorjim_stasheff
- CommentTimeAug 13th 2011
Indeed, Hochschild had no restriction to commutative algebra. `Algebraists like Harrison cohomology' for commutative algebras ONLY in characteristic 0; in general, one needs Andr\'e-Quillen. -
- CommentRowNumber85.
- CommentAuthorMike Shulman
- CommentTimeAug 14th 2011
It’s too bad that we have such an extensive article on the commutative case but nothing about the noncommutative case, when the latter seems a much more natural setting for the definition. I was hoping to find some discussion that might answer a question about constructing the Hochschild complex of a group ring in terms of free loop spaces. I’ll ask it in another thread and maybe someone will know anyway.
-
- CommentRowNumber86.
- CommentAuthorzskoda
- CommentTimeAug 15th 2011
- (edited Aug 15th 2011)
Eventually, it should be organized like cohomology. The special case of abelian sheaf cohomology has a separate entry. But we can split off only once we have enough of general material.
-
- CommentRowNumber87.
- CommentAuthorUrs
- CommentTimeAug 15th 2011
- (edited Aug 15th 2011)
It’s too bad that we have such an extensive article on the commutative case but nothing about the noncommutative case,
On the other hand, it would be worse if we had a non-extensive article on the commutative case and nothing about the noncommutative case. ;-)
Seriously, back then I happened to need the commutative case in great detail, but not the non-commutative case. Sorry.
-
- CommentRowNumber88.
- CommentAuthorMike Shulman
- CommentTimeAug 16th 2011
Sorry.
No need to apologize; wasn’t meant as a criticism of anyone; we all only write about what we need or are interested in. But it might be worthwhile to add a caveat to the existing page warning the reader that it only deals with the commutative case. I suppose I might as well do that now.
-
- CommentRowNumber89.
- CommentAuthorMike Shulman
- CommentTimeAug 28th 2017
The Idea section of Hochschild cohomology appears to claim that the Hochschild homology of with coefficients in itself is the derived center of . But section 1.3 of 0805.0157 says that the derived center is actually the Hochschild cohomology of with coefficients in itself. I assume this was a simple slip on our part, so I will fix it when I get the time.
-
- CommentRowNumber90.
- CommentAuthorMike Shulman
- CommentTimeAug 28th 2017
Also, I think that to define Hochschild homology of a module over a monoid in a monoidal -category, the ambient monoidal -category must be symmetric, since otherwise what does mean? I’ll also fix this.
-
- CommentRowNumber91.
- CommentAuthorMike Shulman
- CommentTimeAug 28th 2017
Anyway, the reason I’m noticing this is that I want to know what to call the analogue of Hochschild (co)homology when the noncommutative algebra is generalized to an enriched category. Essentially the same bar construction makes sense, and from a categorical point of view it just calculates the homotopy coend of a certain profunctor from that category to itself. But do (the homotopy groups of) this coend have a name in the literature? Are they ever just called the “Hochschild homology of the category”? Googling for “Hochschild homology of a category” didn’t turn up anything helpful.
-
- CommentRowNumber92.
- CommentAuthorDavid_Corfield
- CommentTimeAug 28th 2017
- (edited Aug 28th 2017)
The term seems to be in use, such as in this answer to an MO question. There’s also a comment above it
You can take the Hochschild homology of any algebra or category… For categories, there is a similar “bar complex” construction, you can find it for example in Costello’s paper on Calabi-Yau categories. For a more abstract approach, see Toën’s “The homotopy theory of dg categories…”
“Hochschild homology of the category” gets over 8000 hits.
-
- CommentRowNumber93.
- CommentAuthorMike Shulman
- CommentTimeAug 28th 2017
A lot of the hits for “Hochschild homology of a/the category” are bogus/misleading, particularly because people also talk about the Hochschild homology of a monoidal category by treating it as an algebra object in . But using “the” does turn up the MO question you found, which is helpful; I’ll look up those mentioned papers. Thanks!
-
- CommentRowNumber94.
- CommentAuthorUrs
- CommentTimeAug 28th 2017
Thanks for fixing this, Mike.
-
- CommentRowNumber95.
- CommentAuthorDavid_Corfield
- CommentTimeAug 28th 2017
Re #91, are you on the trail of magnitude Hochshild homology, Mike?
-
- CommentRowNumber96.
- CommentAuthorMike Shulman
- CommentTimeAug 28th 2017
Sort of…
-
- CommentRowNumber97.
- CommentAuthorMike Shulman
- CommentTimeAug 28th 2017
Ok, #89 and #90 are fixed.
-
- CommentRowNumber98.
- CommentAuthornLab edit announcer
- CommentTimeOct 29th 2020
Definitions 3.8 and 3.9 were inconsistent with the definition of the Hochschield cochains as the (derived) tensor product with A over the enveloping ring. to fix this I deleted the last term in the definition of the bar complex. (i.e.: If we want to view the bar complex as a free resolution of A over its enveloping ring, we should throw away the last copy of A).
Anonymous
-
- CommentRowNumber99.
- CommentAuthornLab edit announcer
- CommentTimeOct 29th 2020
Definitions 3.8 and 3.9 were inconsistent with the definition of the Hochschield cochains as the (derived) tensor product with A over the enveloping ring. to fix this I deleted the last term in the definition of the bar complex. (i.e.: If we want to view the bar complex as a free resolution of A over its enveloping ring, we should throw away the last copy of A).
Anonymous
-
- CommentRowNumber100.
- CommentAuthorTim_Porter
- CommentTimeJan 16th 2021