Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology definitions deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nforum nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: Kähler differential

Bottom of Page

1 to 28 of 28

  1.  
    • CommentRowNumber1.
    • CommentAuthorUrs
    • CommentTimeJan 26th 2010
    • (edited Jan 26th 2010)

    I spent quite a bit of time now working on the entry Kähler differential

    The motivation was that I had I pointed out the general idea of Kähler differentials at MathOverflow to somebody here. But when I then checked the entry, i found it didn't actually convey the right general picture.

    Have a look at what I did, I did invest quite a bit of time in order to bring both the fully general nonsense nPOV, but lead up to it gently and understandably.

    So there is a big "Idea and definition" section now that is meant to explain what is really going on, in the large and in the small.

    Then the previous content of the entry, on Kähler differentials over ordinary rings and over smooth rings regarded as ordinary rings, I made subsections in a section titled "Specific deifnitions". I added more subsections to this. A stubby one with a pointer to the C^oo-ring case that is discussed in detail at Fermat theory, and then a bit on modules over monoids in general abelian categories, which is what the MO question had been about.

    (They are funny at MO. I think this is quite a deep question. Also Tim Porter pointed out rather non-trivial literature on it. But the poster is being verbally abused for asking a question

    that asks more of the respondent than you have contributed yourself.

    :-o And now they closed down the thread!

    Boy, I am just glad that among us we allow us to ask questions even before we are experts on something. Everything else is unhealthy. )

    Anyway, the section on C^oo rings is a bit short. When you read the entry, you'll notice that there is an obvious question now: "So is it also true for C^oo-rings that the overcat. etc. pp-" The answer is YES, we checked this and it works all very nicely and reproduces the stuff reviewed at Fermat theory precisely. But this has been found / thought about by two graduate students, and I don't want to publicize this too much right now. But later.

    • CommentRowNumber2.
    • CommentAuthorzskoda
    • CommentTimeJan 26th 2010
    • (edited Jan 26th 2010)

    But the Amitsur complex for a coring generalizes to some class of additive comonads.

    More important is to work out the differential calculus internally in categories of sheaves. E.g. for noncommutative algebraic geometry there is a work of Lunts and Rosenberg (the part at MPI preprint, cf. regular differential operator for refs) which centers around "differential monads". This is far more general than the setup in usual algebra.

    I would prefer if we would say ring of smooth function and not smooth ring. Grothendieck introduced literally 17 different notions of smoothness in EGA, so smooth ring for anybody in algebraic geometry has meanings which would lead to different content than what you mean by smooth ring and what is better said a ring of smooth function, in my opinion.

    • CommentRowNumber3.
    • CommentAuthorUrs
    • CommentTimeJan 26th 2010

    I would prefer if we would say ring of smooth function and not smooth ring.

    Okay, right, where I used it, I should say 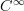C^\infty-ring of smooth functions, to make clear that it is this specific notion of smoothness.

    Concerning the other generalizations you mention: yes, it would be good if we talk about them in the Kähler differential entry, but I don't feel up to that task yet. maybe later, when I studied this a bit more.

    • CommentRowNumber4.
    • CommentAuthorUrs
    • CommentTimeJan 26th 2010

    Hi Zoran,

    in the MO discussion here somebody now also mentions Roserberg's work on Kähler differenials in the noncommutative setup.

    I still have to look into this. Maybe we can have an nLab entry about it? :-) I would be very interested in seeing how that relates to the general Beck/Quillen/Lurie-construction.

    • CommentRowNumber5.
    • CommentAuthorzskoda
    • CommentTimeJan 26th 2010

    I am a bit sick today, but will keep thinking of this task, I think it is very important to see the whole thing from the point of the abelian or stable category of sheaves, instead of the underlying single structured sheaf only.

    • CommentRowNumber6.
    • CommentAuthorTim_Porter
    • CommentTimeMar 5th 2010

    I have added a reference to a new preprint on 'Kähler categories'.

    • CommentRowNumber7.
    • CommentAuthorIan_Durham
    • CommentTimeMar 5th 2010
    This comment is invalid XHTML+MathML+SVG; displaying source. <div> <blockquote>Boy, I am just glad that among us we allow us to ask questions even before we are experts on something. Everything else is unhealthy.</blockquote><br/><br/>And I seriously appreciate it. I personally do not think that "learning" and "research" are mutually exclusive terms, but I didn't have much luck over at MO (I'm sure my somewhat irksome personality didn't help matters). nLab has been really helpful in teaching me the finer points of category theory and in the end will hopefully make me a better researcher. </div>
    • CommentRowNumber8.
    • CommentAuthorUrs
    • CommentTimeMar 5th 2010
    • (edited Mar 5th 2010)

    I have added a reference to a new preprint on 'Kähler categories'.

    Thanks, Tim. I changed your link to one of the author's home page to a direct link to the pdf. Hope that's okay with you.

    Do you know how your "categorical approach" relates to Lurie's notion? For 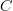C any category / (oo,1)-category whose objects we think of as "rings of functions", he defines the Kähler differentials / cotangent complex assignment to be the left adjoint to the tangent (infinity,1)-category projection. I like that definition. I would like to see how yours relates to that, if it does.

    • CommentRowNumber9.
    • CommentAuthorUrs
    • CommentTimeMar 5th 2010

    Ah, by the way: today I edited a bit the section the problem and its solution.

    • CommentRowNumber10.
    • CommentAuthorTim_Porter
    • CommentTimeMar 6th 2010

    Back one comment: here is a very wild guess. Use (oo,1)-logic to produce a version of linear logic. (This is very worth doing I think) The ideas in BCPS (i.e. the preprint) then should categorise easily, and MUST give something within an epsilon neighbourhood of Lurie's idea. Both are closely linked to the Beck notion of derivation as linked to a slicewise Abelianisation.

    Note that Fox derivatives and not handled by BCPS and that they correspond to the linearisation of homotopy types, (see Menagerie section 3.2. or get a student to give a seminar on it, :-) ) This is related to 'chains on the universal cover', and should fit very neatly into all the machinery, not only in the Kahler case directly.

    • CommentRowNumber11.
    • CommentAuthorUrs
    • CommentTimeMar 6th 2010

    Could you briefly say if and how ordinary Kähler differentials arise as a special case of the BCPS setup?

    • CommentRowNumber12.
    • CommentAuthorTim_Porter
    • CommentTimeMar 6th 2010

    First the BCPS set up is a bit limited as we were concentrating on free algebras. The (co)differential category set up of BCS looked at a differential operator that corresponded to a linearisation. Ander's Koch (and independently me on visit to Ottawa) asked what about Kahler differentials. The BCPS setup shows that under quite mild extra assumptions the construction given in BCS was that of the 'module of Kahler differential' in a classical case. The neat thing is that the BCS differential category setup has several examples that are non-classical.

    To be more definite I would have to consult my copy of the preprint! I will do this soon but need to think out how to explain it (to myself as I worked on this with RIck Blute in 2007!).

    That will give me an excuse to think of the general algebra case as well.

    • CommentRowNumber13.
    • CommentAuthorUrs
    • CommentTimeMar 8th 2010
    • (edited Mar 8th 2010)

    Okay, I would appreciate it. Maybe you could write the basic idea of how your setup reduces to ordinar Kähler differentials in the entry on Kähler differentials.

    • CommentRowNumber14.
    • CommentAuthorTim_Porter
    • CommentTimeMar 8th 2010

    I hope to sometime, but not just now (dentist appointment!) :-)

    • CommentRowNumber15.
    • CommentAuthorUrs
    • CommentTimeMar 8th 2010

    Sure, sure. Just a suggestion. No rush!

    • CommentRowNumber16.
    • CommentAuthorIan_Durham
    • CommentTimeMar 8th 2010
    This comment is invalid XHTML+MathML+SVG; displaying source. <div> <blockquote><br/>(dentist appointment!) :-)<br/></blockquote><br/><br/>:-( </div>
    • CommentRowNumber17.
    • CommentAuthorEric
    • CommentTimeMar 8th 2010

    Come on Tim! Get your priorities straight :)

    • CommentRowNumber18.
    • CommentAuthorzskoda
    • CommentTimeMar 8th 2010

    While the motivation in linear/differential logics in Tim et al. paper is very intringuing (and would like to understand more), I do not see their setup very promising for another target of aplpications: generalized geometry. First of all, the interplay of a free algebra monad with a symmetric tensor product is a very special setup not needed to do the geometry. Second, I consider the interplay with an appropriate notion of a regular differential operator to be very desirable for full geometric power.

    • CommentRowNumber19.
    • CommentAuthorTim_Porter
    • CommentTimeMar 8th 2010

    I have some of the same feelings (and so do the others). The idea grew out of their differential categories stuff. Robin Cockett has some ideas for non-commutative analogues but that will take time. The fascinating idea is that this sort of links up with linear logic in a useful way, but there I would be getting rapidly out of my depth.

    Linearising homotopy types is a nice and related idea. Fox derivatives come in quite naturally there, and they are partially non-commutative in nature.

    I have not yet studied regular differential operators so cannot comment on them.

    • CommentRowNumber20.
    • CommentAuthorzskoda
    • CommentTimeMar 8th 2010
    • (edited Mar 8th 2010)

    I like the claim that you have a connection to the Fox derivative, which is the concept I like very much (including its application to an approach to the Alexander polynomial).

    There is a duality between the filtration on infinitesimals and on regular differential operators (related is the correspondence between crystals of qcoh sheaves and D-modules, and crystals of schemes and D-schemes...). It is interesting what happens if one tries to say alol things not in terms of underlying algebras but in terms of categories of quasicoherent sheaves. The links to the two related MPI preprints of Lunts and Rosenberg can be found at regular differential operators with aim to treat the case of the noncommutative schemes properly.

    • CommentRowNumber21.
    • CommentAuthorTim_Porter
    • CommentTimeMar 8th 2010

    Note I am not saying that the preprint is able to handle the Fox derivative. (That is an aim for future work) The work I am referring to is really due to Dick Crowell (in part) and earlier to Henry Whitehead. Ronnie Brown used this to good effect in his paper with Huebschmann on identities among relations. You form the complex from a group presentation and look at its crossed module (this is the free crossed module on the presentation) . There is a relative Abelianisation process related to that used by Quillen (and derived from Jon Beck's earlier work ) When you apply this to the free crossed module you can write down everything in detail! You get the Fox derivatives and the corresponding Jacobian matrix. I think I did this in the Menagerie, but it is also to do with the relationship between homotopical and homological syzygies as described by Loday. I can give more details if you want, but here is probably not the place. (This is one of the things that I should put on the lab!!!!!)

    • CommentRowNumber22.
    • CommentAuthorzskoda
    • CommentTimeMar 8th 2010

    Recently there has been lots of work on categorification in the quantum group business closely related to knot and link invariants. It would be interesting to see if the "old" approach to knot invariants like the one you mention in modern recast via crossed modules or higher categories could be more directly compared to the categorification approach. The definition of the Alexander polynomial via Fox derivatives and the correspoding Jacobian is too amazing in my opinion to be simply given away in modern generalizations.

    • CommentRowNumber23.
    • CommentAuthorTim_Porter
    • CommentTimeMar 9th 2010

    What is really great fun, is to go back even further in the literature. The usual approach that people go back to is in Crowell and Fox, where they attack the Wirtinger presentation of the know group by means of Fox derivatives. But there is another presentation which is very intuitive and that is Dehn's. If you try out Fox derivatives on that you get very nearly the original Alexander approach to the polynomials. (I know this stuff at the teaching level rather than the research level. It is very approachable by students. There are calculations that are doable and one sees structure in the arrays that reflects certain patterns in the Knot diagrams. Some of this is in Gilbert and Porter, Knots and Surfaces, which was based on the Knot theory course at Bangor (when we existed). I later added more of the calculation stuff as it tested really useful algebraic skills of the students... but I digress!)

    The use of Fox derivatives in the Abelianisation corresponds to chains on the universal cover and is the last part of an infinite sequence of 'pseudo-quotienting' operations on homotopy types. For instance the next one would take a quadratic complex in the sense of Baues and make one more term linear i.e. give the canonical crossed complex associated to it. For each dimension there is a reflective subcategory of homotopy types that are just slight;y more linear than the previous one. The last two correspond to crossed complexes and chain complexs of modules over the fundamental groupoid. I do not know what the corresponding oo-cat picture interprets as. It is, sort-of, higher interchange works but lower interchange may not. Certainly it corresponds to high dimensional Whitehead products vanish but low dimensional ones may not. This can be seen in the simplicial groups models for the connected homotopy types on this approach.

    • CommentRowNumber24.
    • CommentAuthorJohn Baez
    • CommentTimeJan 25th 2022

    In the page Kähler differential the second displayed equation is a formula for multiplication in R⊕NR \oplus N where RR is a commutative ring and NN is an RR-module. This formula looks wrong because the variable rr appears twice at left when we should be multiplying two different elements of R⊕NR \oplus N; also it does not use the RR-module structure of NN. What’s the intended formula? (I can guess one but…)

    • CommentRowNumber25.
    • CommentAuthorTodd_Trimble
    • CommentTimeJan 25th 2022
    • (edited Jan 25th 2022)

    John, I don’t think the article is alleging that this is the ring multiplication on the square-zero extension. There’s some more information at Beck module.

    • CommentRowNumber26.
    • CommentAuthorUrs
    • CommentTimeJan 26th 2022

    The formula in question shows the operation in an abelian group object in the slice of CRingCRing over RR. On the left we have an element in the fiber product over RR, which is why the variable rr appears duplicated. This was probably meant to make it clearer (the text around it seems pretty explicit), though I can see that it can be confusing: But the fiber product object on the left is thus the ring R⊕N⊕NR \oplus N \oplus N.

    • CommentRowNumber27.
    • CommentAuthorJohn Baez
    • CommentTimeJan 26th 2022

    Sorry, I was just confused. It all makes sense.

    • CommentRowNumber28.
    • CommentAuthorDavid_Corfield
    • CommentTimeJan 26th 2022

    There’s some discussion on the page (towards the end of this section) that needs to be removed when we can.

1 to 28 of 28

  1.