nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorJonAwbrey
- CommentTimeSep 14th 2009
- (edited Sep 15th 2009)
A number of ongoing discussions in and around graph of a function are bringing to mind some very old issues in foundations, especially the differences between category-theoretic and set-theoretic practices, but what I see there looks too much in flux at the moment for me to wade into.
So I thought I'd open a space to jot down a few observations as they occur to me.
Top of the list, if I read it right, is that there seems to be some toying around with the idea of identifying functions and relations with their respective graphs, possibly in association with the idea of identifying a subset of a set with its characteristic function.
If I'm reading that wrong, I hope someone will tell me now, as it will save me the effort going further.
Jon
-
- CommentRowNumber2.
- CommentAuthorTobyBartels
- CommentTimeSep 14th 2009
Yeah, both of these things are common identifications to make, but they're incompatible; you don't want to make both of them at once. It's similar to your epigraph at relation theory, I think.
-
- CommentRowNumber3.
- CommentAuthorJonAwbrey
- CommentTimeSep 15th 2009
- (edited Sep 15th 2009)
<p>I am copying this bit of discussion from <a href="http://ncatlab.org/nlab/show/relation+theory">relation theory</a> because I think it's worth going through with some care.</p> <p><em>Relations have types._<br> _Types are functions._<br> _Functions are relations.</em></p> <p>TB: Types are functions?</p> <p>JA: The type of a <img src="/extensions/vLaTeX/cache/latex_33c325191428f6e36401c8b6b1b46bab.png" title="k" style="vertical-align:-20%;" class="tex" alt="k" />-adic relation arrow <img src="/extensions/vLaTeX/cache/latex_43c09e88e076b2d340501a0744aa1639.png" title="f" style="vertical-align:-20%;" class="tex" alt="f" /> in a relation category <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> is its sequence of domains <img src="/extensions/vLaTeX/cache/latex_21ad427bd249ca8ff75ef5e800c23b98.png" title="(\text{dom}_1 f, ..., \text{dom}_k f)" style="vertical-align:-20%;" class="tex" alt="(\text{dom}_1 f, ..., \text{dom}_k f)" />, in other words, the function <img src="/extensions/vLaTeX/cache/latex_efd9be06f6be6ce547491f0f3773333c.png" title="\text{type}_f : [1, k] \to \text{Obj}(C)" style="vertical-align:-20%;" class="tex" alt="\text{type}_f : [1, k] \to \text{Obj}(C)" /> defined by <img src="/extensions/vLaTeX/cache/latex_866cbb373c040a9efa23582847ffb4d1.png" title="\text{type}_f j = \text{dom}_j f" style="vertical-align:-20%;" class="tex" alt="\text{type}_f j = \text{dom}_j f" />.</p> <p>TB: OK, I see! That reminds me of my favourite loop of incompatible interpretations: A function is a kind of relation, a relation is a subset of a cartesian product, a cartesian product is a set of ordered tuples (finite sequences as above), and an ordered tuple is a kind of function. Through this loop, (1,1) (for example) belongs to itself! Another one, which you noticed <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=71">here</a>, is that a function is is a kind of relation, a relation is a kind of subset, and a subset is a kind of function. In fact, a subset is a kind of function in two different ways (an inclusion function and a characteristic function), neither of which matches the original function in this loop.</p> -
- CommentRowNumber4.
- CommentAuthorJonAwbrey
- CommentTimeSep 15th 2009
How do I get math formatting to work in the Forum? -
- CommentRowNumber5.
- CommentAuthorTobyBartels
- CommentTimeSep 15th 2009
- (edited Sep 15th 2009)
- It doesn't work the same as on the wiki, for one thing. But to try things out, put them between double dollar signs. So
-
The type of a <latex>k</latex>-adic relation arrow - becomes
-
‘The type of a
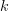 -adic relation arrow’.
-adic relation arrow’.
(Unfortunately, the preview doesn't work and … well, you can see how it looks!)
-
- CommentRowNumber6.
- CommentAuthorTobyBartels
- CommentTimeSep 15th 2009
H'm, it looks like the forum turned my double dollar signs into
<latex>tags. That might be better, since preview seems to work that way too. -
- CommentRowNumber7.
- CommentAuthorJonAwbrey
- CommentTimeSep 15th 2009
- (edited Sep 15th 2009)
Got it — Thanx!
Now where was I ...
Q. When is it valid to regard a relation
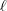 — in particular, a function — as determined by its graph?
— in particular, a function — as determined by its graph?A. Only when the other constituents of the relation, namely, the domains
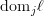 , are determined in context.
, are determined in context. -
- CommentRowNumber8.
- CommentAuthorTobyBartels
- CommentTimeSep 15th 2009
Yes, I agree!
-
- CommentRowNumber9.
- CommentAuthorJonAwbrey
- CommentTimeSep 15th 2009
- (edited Sep 15th 2009)
So a function
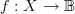 and a function
and a function 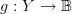 are two different things if
are two different things if 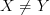 .
.And this is true even if
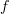 and
and 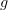 both "indicate" the same set
both "indicate" the same set 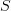 such that
such that 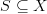 and
and 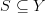 , that is, if
, that is, if 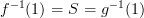 .
.I guess the short way to say it is that there's no such thing as the characteristic function of a set to identify the set with in the first place.
-
- CommentRowNumber10.
- CommentAuthorTobyBartels
- CommentTimeSep 15th 2009
- (edited Sep 15th 2009)
Since I don't believe in a global equality relation on sets (although I can pretend to if necessary), I would say that the question of whether
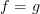 is malformed in this context. And the question of whether their graphs are equal is also malformed.
is malformed in this context. And the question of whether their graphs are equal is also malformed.And indeed, there is no such thing as the characteristic function of a set, only the characteristic function of a subset, that is a set
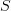 equipped with an injective function from
equipped with an injective function from 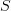 to some other ambient set, such as
to some other ambient set, such as  or
or 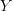 .
.This is the viewpoint of structural set theory.
-
- CommentRowNumber11.
- CommentAuthorJonAwbrey
- CommentTimeSep 15th 2009
- (edited Sep 15th 2009)
Since the world of applications is full of teeny tiny sets that we declare all the time as datatypes and such, I am led to imagine that you can fool some of the computers some of the time into believing that the query
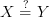 makes sense.
makes sense.I think we are looking at a practical ambiguity in the way we use the formula
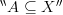 . Sometimes we are talking about a set
. Sometimes we are talking about a set  that just happens to be a subset of
that just happens to be a subset of  , along with many other possible supersets. But sometimes we are really using the syntax
, along with many other possible supersets. But sometimes we are really using the syntax 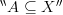 to denote an ordered pair
to denote an ordered pair 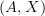 such that
such that 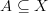 .
. -
- CommentRowNumber12.
- CommentAuthorTobyBartels
- CommentTimeSep 16th 2009
- (edited Sep 16th 2009)
Yes, there is indeed an ambiguity in both ‘
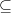 ’ and ‘
’ and ‘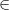 ’. Sometimes they are used as type declarations, and sometimes they are used as propositions.
’. Sometimes they are used as type declarations, and sometimes they are used as propositions.- Even other symbols can be used in this way. Consider ‘
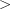 ’ in
’ in 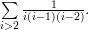
If you write carefully, then this should cause no confusion in practice. The rule is, if the variables in the phrase have all already been given a meaning, then it is a proposition. If not, then it is a type declaration for the new variable. (There should be only one new variable, or something's wrong … except that you can introduce more than one at once if they're separated by commas.)
-
- CommentRowNumber13.
- CommentAuthorJonAwbrey
- CommentTimeSep 16th 2009
I was just now playing in the sandbox with using a form like
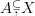 to indicate an ordered pair
to indicate an ordered pair 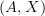 such that
such that 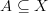 .
. -
- CommentRowNumber14.
- CommentAuthorMike Shulman
- CommentTimeSep 16th 2009
Compounding the confusion is the fact that often logic is not taught using type theory, so that a quantifier like
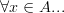 , in which
, in which 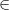 is really a type declaration, is translated into
is really a type declaration, is translated into 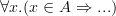 in which it is not. And to treat
in which it is not. And to treat 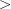 as a type declaration, you probably even need dependent types.
as a type declaration, you probably even need dependent types. -
- CommentRowNumber15.
- CommentAuthorTobyBartels
- CommentTimeSep 16th 2009
Yeah, but it's obvious to me that dependent type theory is the right language for mathematics! (^_^)
-
- CommentRowNumber16.
- CommentAuthorJonAwbrey
- CommentTimeSep 16th 2009
- (edited Sep 16th 2009)
Well, this whole biz of "decontextual" or "dissociated" logic is a fairly recent phenomenon. I don't know if you can really blame Frege, but Russell and Wittgenstein 1.0 are certainly right up there with the prime ⊥etrators.
-
- CommentRowNumber17.
- CommentAuthorJonAwbrey
- CommentTimeSep 25th 2009
- (edited Sep 25th 2009)
I caught brief glimpses of these same old issues — of computability, constructive mathematics, and contextual interpretation — arising again on Neumaier's thread at the Cafe, but the fur was flying too fast and furious for me to keep up there, and everything seemed to fly off in other directions before I could gather my wool to say anything.
So I thought I might try a more leisurely discussion of those focal aspects here.
-
- CommentRowNumber18.
- CommentAuthorJonAwbrey
- CommentTimeSep 25th 2009
- (edited Sep 25th 2009)
I see in Arnold's vision statement an emphasis on computational support for the "actual practice of mathematics". For me, that resonates with one of the first big sea changes in my own view of "automatic theorem proving" back in the late 70s.
I was at that time sorely afflicted with Ulam's Reconstruction Conjecture in graph theory. I had worked out an enumerative approach to the problem — computing orbit sizes under some hairy wreath products — and one of my office mates suggested that a program might be written to brute force a way to the answer. Unfortunate experiences with Fortran and mainframes a decade earlier had turned me off to computational methods, but I was induced to try again with the newfangled tools of Lisp and Pascal and PCs.
To be continued … I'm on the road and having to write in bits and pieces …
Jon
-
- CommentRowNumber19.
- CommentAuthorJonAwbrey
- CommentTimeSep 25th 2009
- (edited Sep 25th 2009)
I never got much further with graph reconstruction, but I did get interested in the general problem of designing systems that could serve in support of mathematical inquiry as mathematicians actually do it.
One of the first things I noticed, as I analyzed the departures of my first simple theorem provers from the ways that most of us would probably go about proving the same sorts of theorems, was the fact that "human-generated proofs" had a much greater role for processes like analogy, case-based reasoning, and learning — broadly speaking, empirical and model-theoretic reasoning — than a purely proof-theoretic prover would run.
Of course, there is nothing that says a computer-generated proof has to be same as a human-generated proof, but when two styles of proof diverge too far from each other — even between different people or between different formal or computational systems — then we still have the problem of communication that needs to be addressed.
Jon
1 to 19 of 19