nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
Atrium > Mathematics, Physics & Philosophy: integration as a Kan extension
Bottom of Page1 to 11 of 11
-
- CommentRowNumber1.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 9th 2010
- (edited Feb 9th 2010)
this came out from a discussion I've recently had with Johan August Alm and Urs Schreiber on path integrals. basic idea is that the space of fields is actually a groupoid (eventually an higher groupoid) and it is this fact to endow it with a canonical measure. so one can integrate functions on it, and to be coherent with the categorical point of view one has adopted, functions on the space of fields should rather be looked at as functors (an insight by Daniel Freed if I'm not wrong here). then integration, i.e. push-forwarding to a point, should be an extension, and one is naturally lead to conjecture that it should be a Kan extension (one would like this extension to be the "optimal" one, i.e. the one keeping most information about the original function).
how does this (very nice, in my opinion) abstract nonsense fit with ordinary integration of differential forms on a manifold ? where's the groupoid? since you're reading this forum, you already know the answer: the involved groupoid is the smooth path groupoid of , and one is taken back to the original naive notion of -differential form: an function measuring (infinitesimal) -volumes. having said "infinitesimal" we have moved from the world of groupids to the one of algebroids, and the algebroid here is the prototipical one: . from this point of view, differential forms on should rather be looked at as -connections with values in , a point of view stressed somewhere by urs in his Lab area (if I didn't misunderstood this). now we have all the ingredients: the groupoid and the functor and we can wonder about Kan extension along the groupoid morphism induced by . how is this related to integration of top-degree forms on ?
a closely realated instance is what happens when we have a group acting on . there the groupoid structure of becomes more complicated, since also the -action comes in. also it seems natural that in this context the push-forward along is replaced by push-forwarding along . so it is natural to wonder: is the natural (Kan extension type, I mean) integration on -manifolds equivariant integration? -
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeFeb 9th 2010
- (edited Feb 9th 2010)
Some old thoughts on this are at Integration without integration (blog, pdf).
I think you need to first transgress, and then push forward.
For instance: take
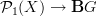 be the parallel transport of a bundle with connection. We may transgress this to loop space by homming the categorical sphere
be the parallel transport of a bundle with connection. We may transgress this to loop space by homming the categorical sphere 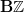 into it
into it![[\mathbf{B}\mathbb{Z},\mathcal{P}_1(X)] = \mathcal{P}_1(\mathcal{L}X) \to G//_{Ad} G [\mathbf{B}\mathbb{Z},\mathcal{P}_1(X)] = \mathcal{P}_1(\mathcal{L}X) \to G//_{Ad} G](/extensions/vLaTeX/cache/latex_3e72cc073386c15085b1a766e77beeed.png) .
.The value of this functor over a loop is the parallel transport around that loop. If
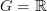 then the original functor encodes a 1-form on X, and the value of the transgressed functor on a loop is the integral of the 1-form around the loop and the functor is locally constant.
then the original functor encodes a 1-form on X, and the value of the transgressed functor on a loop is the integral of the 1-form around the loop and the functor is locally constant.One thing I would like to understand rather sooner than later is how the well-developed theory of push-forward in ordinary differential cohomology -- which is indeed well known to be related to integration -- is expressed in terms of our functorial Yoga. It is a shame that I haven't understood this long ago. But I haven't. I suspect that there is a very simple answer, though, once one has it.
-
- CommentRowNumber3.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 9th 2010
just to be sure it's a typo and not me misundersanding: homming with should give , right? -
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeFeb 9th 2010
- (edited Feb 9th 2010)
well, yes, so
![[\mathbf{B}\mathbb{Z}, \mathcal{P}_1(X)] [\mathbf{B}\mathbb{Z}, \mathcal{P}_1(X)]](/extensions/vLaTeX/cache/latex_05accdacf6fcfb18f8748cae55c46505.png) has
hasas objects smooth loops in X with a chosen point on them
as morphisms path in X between the chosen points of two loops, such that one is the result of conjufating the other by that path.
-
- CommentRowNumber5.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 10th 2010
- (edited Feb 10th 2010)
I've been thinking to the push-forward vs. functorial yoga issue. not much for now, but let me write it here.
on the differential forms side, we may define th pushforward of along a smooth map between compact manifolds by the adjunction formula
for any differential form on .
in order to write this formula in the abstract functorial language of "integration without integration" we just need to identify its ingredients (exept the push-forward, which is what we aim to define). we have
i) differential forms of degree k on a manifold <----> k-functors from to
ii) integration <---> "integration without integration"
iii) pull-back <---> functoriality of
iv) wedge product of forms <---> this is the composition and uses in an essential way the abelianity of and the decompostion of into copies of 's (here is the topological realization of the k-simplex)
howevere there's also another point of view on push-forward of differential forms, which I prefer and which I'll now try to sketch below. -
- CommentRowNumber6.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 10th 2010
- (edited Feb 10th 2010)
let me make an example with fixed dimensions, just to fix ideas: let be a fibration with fiber (here everything is smooth and compact where needed). also assume has dimension 3 and has dimension 2, so that has dimension 1. now let be a 2-form on , which I want to push-forward to . geometric idea of push-forwarding is integration along the fibers, so I'm going to loose 1 dimension and to end up with a 1-form on . what is this 1-form? on general ground, a 1-form on is a representation of the path groupoid of , so it "functorially measures paths in ". but note taht once we're able to measure paths, we're automatically able to measure any 1-dimensional submanifold of . in other words, I'm now tempted to look at a 1-form as a functor from 1-bordism in (actually, this is presumibly a variant of 1-bordism, in which higher morphisms are thin homotopies, but the naive idea will be fine for now). this bordism point of view becomes interesting when we move from to . namely, the 2-form can now be looked at as a functor stemming from the 2-bordism in . so what we need to push-forward is a functor and this is just taking fibers. this indeed reproduces the geometrical definition of pushforward: to know the value of on an infinitesimal path in , one considers the pre-image of in (it is a "cylinder of infinitesimal height"), and integrates the 2-form on this surface. -
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeFeb 10th 2010
- (edited Feb 10th 2010)
Hey Domenico,
nice, good point. Yes. I hadn't really thought about it this way. But I agree, yes, this business may require that we extend along
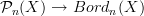 first.
first.Very good point. And that then also makes the connection to quantization become more manifest, because as said elsewhere before, that should somehow be extension along
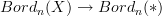 .
.We should follow up on this, this looks promising.
Right now I am still a bit busy with finalizing some aspects on path oo-groupoids. Tomorrow I'll be busy with a seminar on oo-category theory. But then maybe after this I can try to invest some more time into the stuff you are discussing here. Very nice.
-
- CommentRowNumber8.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 10th 2010
- (edited Feb 10th 2010)
I'm glad you enjoyed coming in :-)
don't worry about being busy: I'll be too, till the end of february. after that I'll enjoy investigating in detail the stuff which is emerging here and in the thread on -connections.
later this evening I'll add here something on path-integral quantization of the action given by integration of a 1-form along a 1-path -
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeFeb 10th 2010
later this evening I'll add here
You should rather type this into a page on your web!
-
- CommentRowNumber10.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 10th 2010
- (edited Feb 10th 2010)
yes, I repeat me that every day (that I have to recollect all we've been writing here and in the oo-connections thread, clean it a bit and store it in my web for later use and developement). but then every time there's so much to recollect and so littel to add, and I end up with adding something here.. so let me impose this myself: I'll now sketch the 1-form action path-integral quantization here and then I will stop, and will start recollecting.
let be a 1-form on a manifold . then the action is a functor , and we can naturally extend it to . then path-integral quantization of should be (something related to) the extension of along . since is just the same thing as , if the extension of to has be done "correctly", the functor is a 1-dimensional TQFT (there's surely something to be fixed here, vector spaces arising seems not to be finite dimensional..) and
(a probable way of fixing things is the following: one adds as an external field on a Riemannian metric and considers euclidean bordisms. then one has a function of the real parameter given by integration on the space of loops of length )
ok, enough of this. next post will say "created page..." :-) -
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeFeb 10th 2010
All right. Looking forward to it!
1 to 11 of 11