Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology definitions deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nforum nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

Atrium > Mathematics, Physics & Philosophy: derived category

Bottom of Page

1 to 31 of 31

  1.  
    • CommentRowNumber1.
    • CommentAuthorzskoda
    • CommentTimeFeb 10th 2010
    • (edited Feb 10th 2010)

    I want to continue with Urs discussion on word derived. I argued that the word is not about as he says that

    all one knew was that one could somehow derive one category from another (abelian) category

    as derived category is found in mid 1960-s when "all one knew" was much more than what Urs says. Namely the (classical) derived functors were well-known for a decade before that. Before people had many kinds of cohomology for groups, algebras, Lie algebras etc. and Cartan-Eilenberg found the framework that the sequences of (co)homologies were derived from a single functor once it is put in a framework which they proposed in terms of abelian categories (only). A reason more was also the involvement of differentials; hence deriving a derived functor from a usual functor involved dealing with differential/derivative/boundary kind of terms (that second conotation being very important!!). Thus the whole "deriving" was about functors, not "derived" categories which nobody thought at the time.

    Thus when choosing the term derived category, the word derived meant well-established mathematical meaning of "dealing with derived functors" and not nonmathematical meaning of derived in "deriving from abelian category". While second aspect is true, once one has a mathematical aspect of a term and nonmathematical, the mathematical prevails. You tell me that some map is natural, I immediately think of the commuting square, and I will not use word mathematical otherwise.

    Now when doing first examples of derived geometries, people were again doing moduli spaces, by deriving twice on the left and right, as I epxlained at the cafe.

    • CommentRowNumber2.
    • CommentAuthorUrs
    • CommentTimeFeb 10th 2010
    • (edited Feb 10th 2010)

    Okay, so "derived functors" was first. My comment applies just as well to "derived functor". The term indicates that people "derived one functor from another" without a good concpetual clue as to why one would do that.

    Is "derived" really for "there are differentials involved"? Do you have a reference that demonstrates this historically?

    • CommentRowNumber3.
    • CommentAuthorzskoda
    • CommentTimeFeb 10th 2010

    but I take the point that historically derived functors were considered before derived categories

    Yes. So who decided about why history chose the term ? You or Cartan-Eilenberg ? I have started my article at cafe saying that while your explanation is plausible it is not historically true (plus neglects differential aspect of differential algebra and homological algebra). Therefore it is wrong to say that the people chose word derived becaure the category is derived form abelian. No, but because this was the setting for derived functors, which already had a mathematical meaning. If there was another notion of a setup not coming fomr abelian categories but produced from another kind of data and being a natural setup for derived functors that thing would be called derived category as well. Although it would not be derived in the sense of the question the folk etymology which you propose would like it to be.

    • CommentRowNumber4.
    • CommentAuthorzskoda
    • CommentTimeFeb 10th 2010

    Is "derived" really for "there are differentials involved"? Do you have a reference that demonstrates this historically?

    I read first chapters of Cartan-Eilenberg in my youth of 1987-1988. This was my impression then, and in reading at the time, when I did not know of Verdier (Manin's book and Weibel's book were not around yet and no internet). I think I heard such things in seminars as well. But I do not have a solid proof. Cartan and Eilenberg had another variant, so called satelites. In good cases the sequence of satelites (which are more generally defined) agree with derived functors. In the process indeed one throws out boundary terms at various places and it is hard to believe that it was not in part of that early intuition if it is for an avergae student of old method (like I am).

    • CommentRowNumber5.
    • CommentAuthorzskoda
    • CommentTimeFeb 10th 2010

    The term indicates that people "derived one functor from another" without a good concpetual clue as to why one would do that.

    Come on. The conceptual clue was as good as in 1955 as it is now in 2010. There are exact functors and those which are not exact. More generally there are functors which give bad results on bad objects but there are classes of objects on which they behave nicely, preserving various (typically universal) properties. If you have a bad object you resolve it: the distruibution theory of Schwarz, wavelet analysis and many other field of mathematics do that. The Mittag-Leffler property is one of the standard ways to control the behavour of sequences of aprpoaximations, predates the modern homolopgical algebra and it has applicatiosn in homological algebra as well. Doing satellites which were certain Kan extensions object-by-object or the whole derived functor at once means choosing an admissible class of objects adapted to a functor, so that functor behaves well with respect to them and then applying to a resolution by admissible objects. In very simplest cases, things like fibrant or cofibrant object suffice, but there are many cases when they don't. Now I do not see any conceptual advantage of limiting this philosophy to homotopical setups; moreover homotopical setups place homological and cohomological on the same footing. It is important that there are categories which are suited just for defining right or just for left side of the story and not symmetric like in all Quillen inventions.

    • CommentRowNumber6.
    • CommentAuthorUrs
    • CommentTimeFeb 10th 2010

    there are functors which give bad results on bad objects but there are classes of objects on which they behave nicely, preserving various (typically universal) properties. If you have a bad object you resolve it:

    That's exactly what I mean. This talking about "bad" things shows that people did develop an intuition for what had to be done, but had no clue as to what is going on more abstractly. The problem is that one has gotten so used to this intuition, has developed so much experience, that "bad object" almost feels like a technical term. But really, the term shows lack of conceptual understanding.

    The conceptual clue was as good as in 1955 as it is now in 2010.

    Hm, that seems to be the fundamental point where we disagree. Today we know that passing to a derived functor means extending a given functor to an (oo,1)-functor as faithfully as possible. In retrospect the technology of derived functors is all about building models for morphisms between (oo,1)-categories. A good descriptive term would be one that reflected this fact.

    • CommentRowNumber7.
    • CommentAuthorzskoda
    • CommentTimeFeb 10th 2010
    • (edited Feb 10th 2010)

    Today we know that passing to a derived functor means extending a given functor to an (oo,1)-functor as faithfully as possible.

    Kan extensions are as good as infinity categories for the sense of best approximation. Now if we ask approximations to what -- it was clear then -- to exactness. But infinity categories do NOT explain all the cases homological algebra can do. For example, they always have cofibrant or fibrant resolutions, while in homological algebra you often need adapted admissible classes which are closer to the study of a particular functor than internal feature of the category. Plus the nonabelian one sided generalizations which do not fit into infinity setup like the homological categories of Janelidze or right exact categories of Rosenberg and so on.

    Thus having homotopy which is a symmetric notion forcefully for one sided approximatation from the left or right does not work in all cases.

    Edit: the term derive exact couple apperad in 1950 work of Massey, and denoted the homology of the differential which is the composition of the two maps in the exact couple. This work must have been known to Cartan and Eilenberg.

    • CommentRowNumber8.
    • CommentAuthorzskoda
    • CommentTimeFeb 10th 2010
    • (edited Feb 10th 2010)

    You know I would accept your viewpoint that infinity-categories are better than derived functors if they woudl cover all the cases, but clearly they can not cover the nons-ymmetric cases. The two big ideas agree in the symmetric left-right case when in addition you have sufficiently many fibrant and sufficiently many cofibrant objects. But approximation problem is phrased in 1-categorical setup hence may have solutions even sometimes when the problem is not nicely extedable to Quillen setup.

    Edit: Kontsevich told me that even some of the stuff with stability conditions and zeta functions could be done in about dozen and half examples which he considered with Rosenberg last summer which are in the setup of Rosenberg's triangulated categories. These categories are far from additive and stable in the usual sense and are defined in highly non-symmetric setup. Homotopy is an equivalence relation hence gives symmetric notions in the sense of category theory, passage to opposite category when talking axioms. This restriction is not natural from the point of view of nonabelian nonadditive homological algebra, despite some cases which can be done.

    To notice also there are cases when there is a derived functor where one does not have cocycles in the sense that the obtained objects are not classifying the solutions of equations, i.e. one does not have sections and some algebraic condition on them. This is rare in our standard setups, but often the case e.g. in some monoidal categories of sheaves. Then one doesnot have set-theoretical sections like in Schreier's theory, though still one can have cohomology for the underlying internal groups, Lie algebras etc. If the thing would be algebraic than it owulc correpsond to internal infinity categories in the play, but it isn't. Bressler has shown me several important examples, hard for me to reproduce.

    • CommentRowNumber9.
    • CommentAuthorUrs
    • CommentTimeFeb 10th 2010
    • (edited Feb 10th 2010)

    You may have to remind me of these "non-symmetric cases". All I remember is that last time we talked about it, I didn't get it. Sorry. What does "non-symmetric" exactly mean here?

    • CommentRowNumber10.
    • CommentAuthorUrs
    • CommentTimeFeb 10th 2010

    By the way, I don't feel that the Kan extension definition of derived functor captures their nature much better. Following Mike's query box comment at derived functor.

    What really happens is that we have an oo-category of simplicial objects in an ordinary category (which in abelian cases is equivalently complexes in an abelian category) and that we want to apply our previous 1-functors degreewise. But we have to remember that the oo-category is not in fact spanned by all simplicial objects, but just by the cofibrant-fibrant ones. So if we want to apply our original functor degreewise, we should do it on these objects.

    That's what "deriving" a functor is really all about, I think.

    • CommentRowNumber11.
    • CommentAuthorMike Shulman
    • CommentTimeFeb 11th 2010

    Yeah, I don't like the Kan-extension viewpoint -- it doesn't seem useful and doesn't capture all examples. But is it not true that even in the cases that aren't "left" or "right" one is still doing the general process of "restricting to a subclass of good objects in order to be able to extract an (oo,1)-functor?" Even if the good objects aren't either "left-good" or "right-good" in some formal sense?

    • CommentRowNumber12.
    • CommentAuthorUrs
    • CommentTimeFeb 11th 2010
    • (edited Feb 11th 2010)

    Yes, sure, one does restrict to certain objects. That's what I said: one way to look at it is that one needs to make sure that one applies the functor to an object that is actually part of the (oo,1)-category to which one wants to extend it.

    So of course people did the right thing all along. I am just saying that the term "derived" stems from a time when they didn't know why this is the right thing to do.

    Of course people knew from trial and error that if not done this way, results don't come out as expected.

    Anyway, all this is maybe not so important. It just arose from an attempt to tell Jim Stasheff why people say "derived geometry". Given the carelessness with which people invent terminology, it is not out of the question that if derived functors were only babtized today, somebody would still call them just "derived functors". :-)

    • CommentRowNumber13.
    • CommentAuthorzskoda
    • CommentTimeFeb 11th 2010
    • (edited Feb 11th 2010)

    Urs and Mike, thank you for your interest. I said

    Doing satellites which were certain Kan extensions object-by-object or the whole derived functor at once means choosing an admissible class of objects adapted to a functor, so that functor behaves well with respect to them and then applying to a resolution by admissible objects.

    Here I did NOT say that I looked at derived functors as Kan extensions, what is a separate issue, but that there are satellites and n-th satelite is obtained from n-1-st level by a process involving Kan extension. This can be done even if a functor is not half-exact, unlike the derived functors (of course rarely useful beyond that case). Now this process of forming certain new functors by making closest fits to something depends on 1-categorical properties which we want to extract. Namely this procedure can be vastly generalized much beyond additive categories, by choosing certain class of epimorphisms (or in dual case monomorphisms).

    This talking about "bad" things shows that people did develop an intuition for what had to be done

    So you are claiming that it is done ?? I do not see any significant class of cases which can now be treated which was not in previous era. For example, the sequence of Hopf algebra cocycles including Drinfeld twist and Drinfeld associator found by Majid is not explained by any existing framework of homological algebra so far. The cohomologies in Banach algebra case alike. I know well of about ten of such extremely important cohomologies which do not fit into usual homological or homotopical algebra. People take oldest best understood examples, rephrase them in new language. I appreciate the results, and do not see ANY progress in about a dozen of main examples I was interested in in last 10 years.

    What does "non-symmetric"

    As I said Quillen frameworks have self-dual axioms. Stable categories have shift which is invertible. Quillen exact categories have zero object, and admissible epimorphisms and admissible monomorphisms are treated on the same footing. The dual of a model category is a model category. Homotopy category is obtained via inverting so you get isomorphisms, what is a symmetric notion.Thus if you can define right derived you can define left derived. It appears that to do only left derived functors (in the sense most closely corresponding to universal delta functors of Tohoku) you need much less than model structure on a category. It is for example enough to choose certain kind of singleton Grothendieck cotopology by strict monomorphisms on a category with some colimits to have that part of homological algebra. This is for example done that way in Rosenberg's version of homological algebra. In that case, K-theory can be extended far beyond Quillen exact categories and still having universality in the sense of Tohoku (for Quillen's traditional definition this is not known as he passes through classifying spaces what is rather indirect way, not close to universalities in categorical sense).

    Having Dold-Kan in good cases like abelian and semiabelian category can make the homological algebra based on resolving by complexes by resolving by simplicial things. There are many kinds of higher categorical structures, the (infinity,1)-categories have a special role in a world of examples, very close to symmetric. I have seen no case that it explains cohomologies for structures living in 1-categories which are far from such, while other frameworks do exist.

    • CommentRowNumber14.
    • CommentAuthorzskoda
    • CommentTimeFeb 11th 2010

    But is it not true that even in the cases that aren't "left" or "right" one is still doing the general process of "restricting to a subclass of good objects in order to be able to extract an (oo,1)-functor?"

    How can I know ? Experts in infinity categories like you yawn once one mentions nonstable (in the sense of homotopy), nonbalanced, noncommutative, no zero object, covers nonstable under pullbacks and alike circumstances, typical of noncommutative algebra and functional analysis. I do not know what infinity,1-functor means in such situations.

    • CommentRowNumber15.
    • CommentAuthorzskoda
    • CommentTimeFeb 12th 2010

    But we have to remember that the oo-category is not in fact spanned by all simplicial objects, but just by the cofibrant-fibrant ones. So if we want to apply our original functor degreewise, we should do it on these objects.

    Do you know adapted classes ? They are used even in abelian homological algebra when there is no cofibrant or fibrant objects. They are adapted to a single functor. This is very symmetric situation and even here this philosophy does not quite work.

    • CommentRowNumber16.
    • CommentAuthorzskoda
    • CommentTimeFeb 12th 2010

    By the way I just looked at the 1950 paper of Massey where he defined derived couple. He takes for granted that people know what is a derived group of a differential group. Differential group was at the time an abelian group with endomorphism of square zero, called differential. Homology of the differential was called derived group. This terminology is taken for granted there. This predates derived functors.

    • CommentRowNumber17.
    • CommentAuthorMike Shulman
    • CommentTimeFeb 12th 2010

    Zoran, please don't tell me that I yawn when, in fact, I do not. I definitely think that more general sorts of derived functors are interesting, and I'd like to know whether they fit into an (oo,1)-categorical framework. (I think they might in ways that their users don't realize, but I have no a priori belief that they must.) I don't know what I ever said to make you think that I prefer things to be stable, commutative, balanced, or have zero objects. Of course, nothing in model category theory requires things to be stable, commutative, balanced, or have zero objects either. But I certainly agree that there are plenty of situations not covered by model category theory. You seem to be saying that in these situations, there is not even a relevant notion of weak equivalence?

    • CommentRowNumber18.
    • CommentAuthorzskoda
    • CommentTimeFeb 12th 2010

    @Mike: I did not mean it personally, but indeed the knowledgeable community of experts, and I consider you an expert, does in large yawn at it; too few pay attention. I would not write it, if I were not intentionally trying to provoke some interest; we might disagree in the scale of importance of what I am saying. Maybe it would be counterproductive to you personally to go against the mainstream in your field, but I think that eventually reward for practical mathematics would be large.

    You seem to be saying that in these situations, there is not even a relevant notion of weak equivalence

    I can not claim that. If it is true can know for sure WHICH of the not-so-understood examples do not fit into some sort of approach CENTERED on weak equivalence. I would guess that weak equivalence would still be around but that the naive homotopy category would tell too little in comparison with the classical case. But there are strong indications that much of the symmetry is lost (e.g. one sided localizations). One approach (unpublished) to a generalization of one-sided homological algebra for example is based on fibered categories and the chasing of elements is replaced by chasing of cartesian squares in the fibered category sense (the fiber over an object is a generalization of all singleton covers of that object in appropriate Grothendieck pretopology).

    I'd prefer to discuss examples than such a generality.

    @Urs

    If we have a (infty,1)-adjunction at the level of simplicial nerves of some model categories, does the adjunction by general nonsense decategorify or, better strictify, to usual adjunction for underlying 1-categories, in general ? How the coherent homotopy units and counits become strict ?

    • CommentRowNumber19.
    • CommentAuthorUrs
    • CommentTimeFeb 12th 2010

    Zoran,

    yes , (oo,1)-adjunctions correspond to Quillen adjunctions. That's a theorem in HTT somewhere in the section on adoint (oo,1)-functors. But I can't look it up right now.

    • CommentRowNumber20.
    • CommentAuthorzskoda
    • CommentTimeFeb 12th 2010

    Good. I'll look it up (I knew one direction before that Quillen adjunctions imply the infinity adjunctions, but not that every infinity adjunction for infinity categories coming from model categories comes from a genuine Quillen adjunction).

    • CommentRowNumber21.
    • CommentAuthorUrs
    • CommentTimeFeb 13th 2010

    I hope I am remembering this correctly. I'll check...

    • CommentRowNumber22.
    • CommentAuthorUrs
    • CommentTimeFeb 13th 2010

    Okay, it' s prop. 5.2.4.6, just one way: Quillen adjunction models an (oo,1)-adjunction.

    Notice the remark 5.2.4.7 right below that on derived functors.

    • CommentRowNumber23.
    • CommentAuthorUrs
    • CommentTimeFeb 13th 2010

    Concerning the non-symmetry:

    It appears that to do only left derived functors (in the sense most closely corresponding to universal delta functors of Tohoku) you need much less than model structure on a category.

    Sure, to speak about derived functors all you need is a category with weak equivalences! Nothing else.

    A category with weak equivalences alone determines an (oo,1)-category and every (oo,1)-category is determined by a category with weak equivalences.

    Model categories are just there to provide a bit more structure to handle this.

    • CommentRowNumber24.
    • CommentAuthorzskoda
    • CommentTimeFeb 13th 2010

    I know that model categories are just tool to provide the existence of localization at weak equivalences. But in nonsymmetric examples I know it seems that localizing, irrespective of niceties of its description and existence is too rude and can destroy essential nonsymmetric nature of the structure. Talking infinity categories and having all examples in almost symmetric world is self-deceit. For light examples, try to explain bialgebra cocycles or prove that higher K-theory for Quillen exact categories (what is still symmetric, but in the right direction) as components of a derived functor. Quillen had an ad hoc construction and homotopy theorists are happy. I can believe in something only if it solves a universal problem.

    • CommentRowNumber25.
    • CommentAuthorUrs
    • CommentTimeFeb 15th 2010
    • (edited Feb 15th 2010)

    okay, it would be good to better understand that example. I am just not sure if from one ill-understood potential application one should already deduce that it can't fit into (oo,1)-category theory. Also, two of the three special cases of bialgebra cocycles that are listed at the entry we do know well fit into (oo,1)-category theory!

    And the argument that there is no model structure known for that example but just some other homotopical category due to some non-symmetry is not a compelling argument that there can't be one.

    My intuition by looking at that page is that there should be a good (oo,1)-categorical description. That 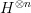H^{\otimes n} looks a bit like a bar complex resolution or something like this. I would be very surprised if this does not have a nice explanation in an (oo,1)-category.

    But of course for that claim, too, I have curently no proof.

    • CommentRowNumber26.
    • CommentAuthorzskoda
    • CommentTimeFeb 15th 2010

    Also, two of the three special cases of bialgebra cocycles that are listed at the entry we do know well fit into (oo,1)-category theory!

    Come on, these are abelian, symmetric special cases. Just an argument that the general formula is meaningful (the wide presence of Drinfeld cocycle and Drinfeld associator being among othhers).

    But Rosenberg's nonabelian homologiocal algebra is not an EXAMPLE but the whole clean and very simple framework, and that whole framework does not fit for example.

    After 30 years nobody found even K-theory for Quillen exact categories to be universal.

    You call these sporadic examples ???

    I would be very surprised if this does not have a nice explanation in an (oo,1)-category.

    Look infinity categories in algebra are widely used for 20 years, mainly as pretraingulated DG-categories (1989 on), or A infinity (1993 on). 20 years and almost no results beyond almost symmetric cases.

    • CommentRowNumber27.
    • CommentAuthorzskoda
    • CommentTimeFeb 15th 2010
    • (edited Feb 15th 2010)

    And the argument that there is no model structure known for that example but just some other homotopical category due to some non-symmetry is not a compelling argument that there can't be one.

    The thing is that if we had it, than both the left and right derived functors would have sense simultaneously. But one of them builds on admissible epis and another on admissible monos. That is why one does not expect homotopical categories.

    Edit: for many years, I suspect that the responsible structures for things lke bialgebra cocycles (but less sure about some other examples) are some analogues of (higher) categorical algebra internal to some noncartesian monoidal categories. You know by loosing universality of cartesian products you loose a lot, but there may be more complicated mechanisms to retain some of the story. There is extremely little known even on 1-categories in this setup. Another direction is to do sheaf-like conditions not only for covers but for more exotic types of cones. There is very few works even touching on that possibility.

    • CommentRowNumber28.
    • CommentAuthorUrs
    • CommentTimeFeb 15th 2010
    • (edited Feb 15th 2010)

    I would be really interested in discussing and understanding these things in more detail, eventually.

    Have you every looked at HTT section 5.5.8 titled "Nonabelian Derived Categories"? And maybe the following subsection?

    In particular, maybe search these two sections for the term "derived functor" (it appears twice) and please let me know if this might be at all related to the nonabelian non-symmetric situations that you have in mind.

    • CommentRowNumber29.
    • CommentAuthorMike Shulman
    • CommentTimeFeb 15th 2010

    I haven't thought about the bialgebra cocycles yet, but my preferred meaning of "derived functor" is not "handed," although it does use weak equivalences. Say C and D are homotopical categories and f:C-->D is a functor. A derived functor of f is specified by giving an endofunctor, say q, of C, which is connected to the identity by a natural zigzag of weak equivalences, and such that the composite fq preserves weak equivalences. There is then induced an (oo,1)-functor between the localizations of C and D, by applying the universal property of the localization to fq. If the zigzag connecting q to the identity consists of only one arrow, then the derived functor is "left" or "right" according to which direction the arrow goes in, but in general it need not be either.

    For example, if C and D are (say) topologically enriched model categories and f is any topologically enriched functor, then q can be taken to be a fibrant+cofibrant replacement functor, which is connected to the identity by a length-two zigzag of weak equivalences. Since weak equivalences between fibrant+cofibrant objects in a topological model category are homotopy equivalences, which are preserved by any topological functor, fq preserves weak equivalences and thus f has a derived functor. Note that f need not be left or right Quillen, have any adjoints, or interact with cofibrations or fibrations at all. The same argument works in algebraic cases, for instance if C and D are abelian categories such that Ch(C) and Ch(D) have model structures, and f is any additive functor, then Ch(f) preserves weak equivalences (=quasi-isomorphisms) between fibrant+cofibrant chain complexes (those being simply chain homotopy equivalences, which are preserved by any Ch-enriched functor) and thus has a derived functor. It seems at least possible to me that some of the non-handed "derived functors" in algebra could be obtained in this way, but I haven't thought about specific cases.

    • CommentRowNumber30.
    • CommentAuthorUrs
    • CommentTimeFeb 15th 2010

    I was busy rewriting derived functor. But I am running out of steam now.

    • CommentRowNumber31.
    • CommentAuthorzskoda
    • CommentTimeFeb 18th 2010
    • (edited Feb 18th 2010)

    To Mike: Surely, I agree that many cases of sided derived functors will be eventually absorbed into homotopical categories formalism. For example, maybe Bourn's Dold-Kan for semiabelian setup can help us with semiabelian case (though in that case we have the zero object, and osme other symmetries, what we can not afford in most of applications I have in mind!). We agree that the homotopical contexts can be viewed as a structure on a 1-category. In Quillen exact categories one has a structure of admissible epis and admissible monos. There are formalisms, like Rosenberg's with motivation in noncommutative algebra and geometry, where one has just half of such structure, just admissible epis or just admissible monos. And then the derived functors of one side make manifestly sense (not quite trivial, the solution looks easy but there are subtleties involved). One can go beyond that and look just at fibered or cofibered categories as two sides in greater generality.

    To Urs: yes I have seen nonabelian derived categories, now I don't recall quite what was it, but I recall it was far from what I would like to. I will look again, thanks.

    Edit: Most of the time we are used to have something like Dold-Kan. However there are situations where complexes make sense and there is no Dold-Kan and no zero objects. Just initial or just terminal object, depending on side. Then one can not pass to homotopy groups, but needs to stay at the complex side. This looks similar, especially combinatorially to higher categories, as one needs to use various universalities when dealing with resolutions and satellites, so it is analogous to an extent, but also highly nonsymmetric.

1 to 31 of 31

  1.