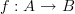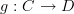nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
Atrium > Mathematics, Physics & Philosophy: Question: components of a natural transformation
Bottom of Page1 to 9 of 9
-
- CommentRowNumber1.
- CommentAuthorEric
- CommentTimeFeb 21st 2010
- (edited Feb 21st 2010)
Given functors
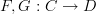 , a natural transformation
, a natural transformation 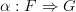 involves components
involves components 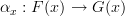 .
.Is it necessary that these components already live in
 or can they be added as part of the definition of
or can they be added as part of the definition of 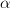 ?
?Edit: I wasn't sure if I should put this in a query box on the nLab. I'm a little rusty.
Edit^2: For example,
Let
 consist of two objects and one morphism
consist of two objects and one morphism 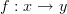 . Let
. Let  consist of four objects and two morphisms
consist of four objects and two morphisms 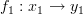 ,
, 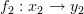 . We could have two functors
. We could have two functors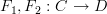
with
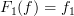 and
and 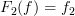 .
.Would we just say there are no natural transformations
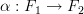 or could we allow
or could we allow 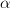 to bring along two morphisms
to bring along two morphisms 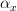 ,
, 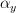 with it?
with it? -
- CommentRowNumber2.
- CommentAuthorHarry Gindi
- CommentTimeFeb 21st 2010
No. The natural transformation diagram has to commute. It's similar to the condition on a morphism of chain complexes.
-
- CommentRowNumber3.
- CommentAuthorSridharRamesh
- CommentTimeFeb 21st 2010
- (edited Feb 21st 2010)
Basically, the answer is "The components have to already live in D". There are no natural transformations between $F_1$ and $F_2$. Whatever you mean by "bring along morphisms", that would be another notion, but it might still be interesting and useful, if you flesh it out further. (Although, it also might not be, so much...) -
- CommentRowNumber4.
- CommentAuthorEric
- CommentTimeFeb 21st 2010
- (edited Feb 21st 2010)
@Sridhar: Thanks. That is what I thought the answer might be. Too bad.
I'm trying to flesh this out (to the best of meager abilities) at natural transformation (discussion). Help much appreciated! :) I'm probably on a dead end road, but by the time I discover that, I will hopefully have learned a thing or two. Basically, I was a little uncomfortable with the fact that natural transformations were defined only for functors sharing the same domain and codomain. In trying to see if I could cook up a slightly different natural transformation-like concept, I settled on the diagram there. I liked the idea enough to try to reduce the dimension by 1 and think of functors as special kind of natural transformation. Then maybe a morphism is a special kind of functor. Etc...
In a way, a cograph of a functor involves "bring(ing) along morphism" so I don't think the idea is entirely outlandish, I just need to find the right way to express it. Again, any ideas would be greatly appreciated.
Edit: There are also traces of discussion at Natural Transformation (ericforgy) and functor (discussion).
-
- CommentRowNumber5.
- CommentAuthorHarry Gindi
- CommentTimeFeb 21st 2010
- (edited Feb 21st 2010)
The reason that natural transformations have to share the same domain/codomain is that they're 2-morphisms in the category of categories. That is, we can assign to each pair of categories a functor category, and natural transformations are the morphisms in the functor category. I believe there are notions similar to what you're talking about using something called a double category, but I could be horribly wrong.
-
- CommentRowNumber6.
- CommentAuthorEric
- CommentTimeFeb 21st 2010
- (edited Feb 21st 2010)
<p>Thanks Harry.</p> <p>It's interesting you bring up the category of categories because that is one possible direction I was headed with this.</p> <p>If natural transformations are 2-morphisms in the category of categories <a href="https://ncatlab.org/nlab/show/Cat">Cat</a>, i.e. bigons, what would be morphisms in the <a href="https://ncatlab.org/nlab/show/arrow+category">arrow category</a> of categories <img src="/extensions/vLaTeX/cache/latex_8b821b5ca328916550542edf98843025.png" title="Arr(Cat)" style="vertical-align:-20%;" class="tex" alt="Arr(Cat)" />. In <img src="/extensions/vLaTeX/cache/latex_8b821b5ca328916550542edf98843025.png" title="Arr(Cat)" style="vertical-align:-20%;" class="tex" alt="Arr(Cat)" />, unless I'm confused, objects would be functors but not necessarily with the same domain and codomain, i.e. we could have two objects</p> <p><img src="/extensions/vLaTeX/cache/latex_733c874c86b3eec3e9369a1846cb8672.png" title="F:A\to B" style="vertical-align:-20%;" class="tex" alt="F:A\to B" /><br></p> <img src="/extensions/vLaTeX/cache/latex_8467478d932a698e54905aa014665e65.png" title="G:C\to D" style="vertical-align:-20%;" class="tex" alt="G:C\to D" /> <p>where <img src="/extensions/vLaTeX/cache/latex_b754fe221a079c2ca5127d6ad18f886a.png" title="A" style="vertical-align:-20%;" class="tex" alt="A" />, <img src="/extensions/vLaTeX/cache/latex_525eb65281c6d3b0bfacfe7567f8af85.png" title="B" style="vertical-align:-20%;" class="tex" alt="B" />, <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" />, <img src="/extensions/vLaTeX/cache/latex_2741ee6cf4a5aa48b2ee29b3b0fee62e.png" title="D" style="vertical-align:-20%;" class="tex" alt="D" /> are distinct categories. What I am trying to describe (I think) would be morphisms between these. These morphisms would be commuting squares (of functors) like the one at <a href="https://ncatlab.org/nlab/show/natural+transformation+%28discussion%29">natural transformation (discussion)</a>.</p> -
- CommentRowNumber7.
- CommentAuthorHarry Gindi
- CommentTimeFeb 21st 2010
Ah yes, that's related to the "walking arrow", where you can compose 2-morphisms in a weird way by "messing around" with this walking arrow. The notion of a natural transformation that we have seems to be the right one, at least in the 2-category Cat.
-
- CommentRowNumber8.
- CommentAuthorEric
- CommentTimeFeb 21st 2010
- (edited Feb 21st 2010)
I drew a diagram at Arrow Category of Categories (ericforgy). It is a little messy, but the point is there are three morphisms
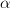 ,
, 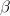 ,
, 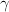 in the arrow category consisting of 4 objects
in the arrow category consisting of 4 objects[Note: There are also composite morphisms
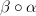 and
and 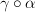 that I didn't draw.]
that I didn't draw.]I think this is a little different than a double category because the 2-paths can branch as indicated. Does a double category allow this kind of "branching" of 2-paths?
-
- CommentRowNumber9.
- CommentAuthorSridharRamesh
- CommentTimeFeb 21st 2010
- (edited Feb 21st 2010)
I'm not sure I understand the diagram you drew. What are the codomains of
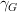 and
and 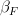 ?
?Edit: Nevermind, I get it now; they'd be G and F, respectively.
1 to 9 of 9