nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorEric
- CommentTimeSep 25th 2009
- (edited Apr 8th 2010)
I have many questions about directed spaces, but thought I’d try starting a discussion here rather than dropping a ton of query boxes on directed space.
We should be able to define directed chains on directed spaces in such a way that the boundary of a -chain should be a -chain.
It seems like the boundary of a directed -chain can be decomposed into three pieces:
- a directed -chain with paths flowing out of it but none flowing into it (i.e. the “beginning” chain)
- a directed -chain with paths flowing into it but none flowing out (i.e. the “end” chain)
- a directed -chain with paths flowing into and out of it (i.e. the “interior” chain)
The three components have the property that
- every point of the directed -chain is “causally connected” to some point on the beginning directed -chain
- every point of the directed -chain is “causally connected” to some point of the end directed -chain
A neat image entering my mind is that of Huygen’s principle. It is as if each point of the directed -cell sends out a scouting party in all forward directions. The beginning directed chain is the minimal set of points for which the scouting parting will touch every point of the original directed chain. The end directed chain is the set of points where the scouting party reaches a dead end.
-
- CommentRowNumber2.
- CommentAuthorTim_Porter
- CommentTimeSep 30th 2010
- (edited Sep 30th 2010)
@Urs As this already exists, courtesy of Eric, lets use it to continue the discussion. I have put references on that new entry. (They were just copied from the directed homotopy entry.) I think your definition is more or less the same as the one that I gave in the Dagstuhl paper. (<- listed in those references.)
I would be very interested in seeing the future and past tangent spaces of such a model from your viewpoint. (For the moment links would suffice.) I have been trying to see this for other purposes, and in more generality, relating to rewriting (joint work with Philippe Malbos and Yves Guiraud), but that does not only explicitly handle directed things so I won’t talk more about that for the moment until we are more advanced on it.
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeSep 30th 2010
- (edited Sep 30th 2010)
more or less the same as the one that I gave in the Dagstuhl paper.
Does everybody know what “the Dagstuhl paper” refers to?
I am looking at this one: Enriched categories and models for spaces of dipaths.
It seems to me that a central difference between your and Grandis’ definitions and what I proposed at fundamental infinity-category is that you require 2-cells to consist of paths of directed paths.
Is that necessary?
Eventually the right definition will be determined by the properties and theorems that it induces. I have been looking at survey’s by Grandis, but I have trouble identifying what the central statements of “directed homotopy theory” so far are. Can you help me?
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeSep 30th 2010
Does your definition give a Kan-complex enriched category of paths in a directed space?
-
- CommentRowNumber5.
- CommentAuthorTim_Porter
- CommentTimeSep 30th 2010
Sorry I forgot to mention which paper on that site as it was the only one by me. :(
I used directed forms of the topological n-simplex (as you noticed), and I believe that this gives the same thing up to equivalence as your version using spines. More exactly, my methods did not require paths of paths to be directed, it allows that as one possibility.
I think that central statements are not yet definitive enough in that area. Marco’s book is interesting but apart from some very neat results on fundamental categories and the sense in which they should have minimal models, much of the rest of the book is setting up background abstract directed homotopy applicable in various contexts. The point he seems to be making is that you need directed models of chain complexes etc, so as to be sure which invariants are going to give you information in the various types of situation that he is considering.
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeSep 30th 2010
I believe that this gives the same thing up to equivalence as your version using spines.
How do you see this? This would be good to write out!
Also, related to that, could you remind me: with your definition, what kind of simplicially enriched category exactly do you get from a directed space? Is it automatically Kan-complex enriched? In the case that the space is undirected, is the homotopy coherent nerve of your simplicially enriched category obtained from it equivalent to the standard singular simplicial complex? (Maybe that’s evident, i don’t have your article in front of me right now.)
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeSep 30th 2010
I would be very interested in seeing the future and past tangent spaces of such a model from your viewpoint.
There is a general abstract answer to this:
when we place ourselves in a smooth topos (such as sheaves over duals of -rings), then we can restate the definition of fundamental -category that I gave verbatim with all simplices in the directed space being infinitesimal. You then get the -category version of Kock’s -groupoid of infinitesimal paths. This is the tangent bundle in its incarnation as the tangent Lie algebroid and that in turn regarded as an -Lie algebroid. So here we get the corresponding directed tangent -Lie algebroid: at each point of the space it contains just the space of future-directed vectors.
-
- CommentRowNumber8.
- CommentAuthorTim_Porter
- CommentTimeSep 30th 2010
I have to think of what I did. I seem to remember essentially using ordered prisms with the two ends mapped to the objects concerned. (I was working in a pospace in the more ’traditional’ sense of a space with a closed partial order on it.) I used a Moore category type construction, using concatenation, and so replaced the by a directed line of length , and then normalised at the end. This gives a -enriched category not a more general quasicat. I think it is quasi-cat enriched.
Is this in some sense equivalent to your construction (at least for the pospace case). My feeling is that there is a joint quasicat which contains both and for which the inclusions are deformation retractions but these probably do not preserve order in some sense. My prisms are made up of prisms within your structure I think, and any of your simplices is homotopic (within your structure) to one which is represented by a directed n-simplex in my sense, i.e. a dimap from the directed n-simplex to the pospace, (and here I am not 100% sure). There will be 1-simplices in my structure that are not directly linked in mine but for which the corresponding construct in yours will give a linkage. (i.e. they are joined by a zigzag in mine.) Thinking about it a bit more makes me think that there are subtleties that may mean the two structures are not equivalent in the strongest sense possible but may be in some weaker sense.
I feel that it is useful to distinguish dipaths using directed 2-cells (and higher) but once that is done, one can invert from some level onwards so as to get something more computable.
I think that there may be other structures than the one you outline that keep more of the order information for longer. Having almost finished reading Marco’s book I am sure there is still a lot of hard thinking to do on directed homotopy. He has some excellent ideas and some good counterexamples to too simplistic ideas. (The paper you link to already has some of these in I think.)
-
- CommentRowNumber9.
- CommentAuthorTim_Porter
- CommentTimeSep 30th 2010
That was a reply to an earlier question now I see number 7. I was sort of trying to get a future simplicial cone idea and to avoid non-discrete models at least until I got my head around that earlier idea. Marco has some very good thoughts about that in his central sections but in a slightly different context. My thought is that in an evolving space or pospace, one wants the possibility that the group of a ’bundle’ may evolve with the space. This suggests various models one of which is the use of the factorisation category or twisted arrow category of the underlying ’category’. I noted that Wells in his 1979 notes on extensions of categories ends up using that construction. The idea of having a bundle over the basic -cat as being an extension in a similar way is possibly interesting, but i am still exploring the implications of Wells’ ideas. (I linked to his paper from the entry on Baues-Wirshing cohomology, but have not yet got around to writing up some entry on his ideas.) How to go from that to an infinitesimal structure should by then be clear (or at least clearer!)
-
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeSep 30th 2010
I think it is quasi-cat enriched.
Ah, it’s an -category that you construct. That would make sense, given that you require diected paths and also directed homotopies.
How do you define the higher homotopies?
-
- CommentRowNumber11.
- CommentAuthorDavidRoberts
- CommentTimeOct 1st 2010
I should point out there seems a little bit of confusion between 1. directed 2-paths and 2. paths of dipaths. At one point on the other thread Urs has homotopies of dipaths that were not through dipaths. This is surely a mistake. Then he says
you require 2-cells to consist of paths of directed paths.
this is 2. above. But having homotopies though dipaths does not make the homotopies themselves non-invertible, unless one uses the directed interval to form the homotopies. From this one should get an (oo,1)-category. Then Tim replied
my methods did not require paths of paths to be directed, it allows that as one possibility.
but this is 1. above, and I agree that this will give an (oo,2)-category.
Just to clarify…
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeOct 1st 2010
- (edited Oct 1st 2010)
At one point on the other thread Urs has homotopies of dipaths that were not through dipaths. This is surely a mistake.
Let’s see, what is a mistake? Is there a mistake in the statement at fundamental (infinity,1)-category?
-
- CommentRowNumber13.
- CommentAuthorEric
- CommentTimeOct 1st 2010
Comment #12 seems to be related to my diamonation (ericforgy) conjecture I think. Diamonds are, almost by definition, directed (finite) spaces and you can always fill a diamond with directed simplices. So if any directed space can be diamonated, then… something… :)
Speaking of which, I just changed the wording of the conjecture. Now it reads:
Just as any smooth manifold can be triangulated, any smooth directed space can be diamonated.
-
- CommentRowNumber14.
- CommentAuthorTim_Porter
- CommentTimeOct 1st 2010
@David. My point was that my approach allowed different models of the directed n-simplex to be used, and different models give different theories. The relationships between the models for the simplex then allow one to compare the theories (not in any deep sense but nice and naively :-))
-
- CommentRowNumber15.
- CommentAuthorTim_Porter
- CommentTimeOct 1st 2010
Some time ago, when in Ottawa, Rick Blute, Marc Comeau and myself started looking at AQFTs but with dagger categories as the values. There were further discussions with Samson Abramsky and the group at Oxford, but the paper is still ’draft’. Some ideas on this can be gleaned from Bob Coecke’s article, which is worth looking at anyway.
-
- CommentRowNumber16.
- CommentAuthorTim_Porter
- CommentTimeOct 1st 2010
- (edited Oct 1st 2010)
BTW as all of this is about ’evolution of evolution’ or ’evolving spaces’ etc., it does seem to me, and has been in the background of my thoughts for some time, that we do need (i) to remember feedback and (ii) look for non-physical systems to model, (especially Azimuthal ones :-) perhaps).
In other words, our directed spaces need to be very general in their intuitive impact and limited ’rollback’ and ’feedback’ need building in. They should include models of ’processes’ in good generality and eventually involve probabilistic aspects. ….. but that is perhaps a long way ahead, or is it. This stuff has been fascinating me for years!
-
- CommentRowNumber17.
- CommentAuthorDavidRoberts
- CommentTimeOct 1st 2010
- (edited Oct 1st 2010)
Let’s see, what is a mistake?
well, that’s too strong a word. I meant that letting two dipaths be homotopic even through intermediate paths which are not themselves directed seems to be the wrong spirit of things. For instance, it means that homotopies are not (ordinary) paths in the space of dipaths. As to the page fundamental (infinity,1)-category, I am neutral.
-
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeOct 1st 2010
- (edited Oct 1st 2010)
I meant that letting two dipaths be homotopic even through intermediate paths which are not themselves directed seems to be the wrong spirit of things.
I think oppositely. And I have a reason:
the canonical source of directed spaces is the geometric realization of quasi-categories, with directed paths precisely those that factor orientation-preservingly through their 1-skeleton.
To have any chance to recover the quasicategory as the fundamental oo,1-category of thi space, we must not demand that 2-cells are paths of directed paths.
-
- CommentRowNumber19.
- CommentAuthorTim_Porter
- CommentTimeOct 1st 2010
@Urs ’the canonical source of directed spaces’?????? There are lots of applications that have a general need for a directed space, yet in which the 2-cells are NOT as you suggest. Aren’t you reasoning in a circle?
-
- CommentRowNumber20.
- CommentAuthorEric
- CommentTimeOct 1st 2010
- (edited Oct 1st 2010)
Comment #18 almost seems like you are assuming an answer and trying to reverse engineer the foundations that gives the answer you want.
What do you end up with as the fundamental -category by doing things in the “right spirit”? If it is not the quasicategory, it might still be interesting. It could even be that the fundamental -category is not in the “right spirit” either.
My tendency would be to give up on quasicategories before I’d give up something so holy as causality, but maybe I’m letting my biases get in the way.
Edit: Oops. I was writing my comment when Tim posted his, so I didn’t see his until after posting mine.
-
- CommentRowNumber21.
- CommentAuthorTim_Porter
- CommentTimeOct 1st 2010
- (edited Oct 1st 2010)
@Eric :-) !!! There should be a range of models of -categories and each will fit some parts of the processes / causality scenery, hence my model did not require using ordered simplexes as the arguments work anyway but they can be applied with that assumption.
-
- CommentRowNumber22.
- CommentAuthorUrs
- CommentTimeOct 1st 2010
Aren’t you reasoning in a circle?
No. If there is going to be any good “directed homotopy theory” then directed paths need to be like morphisms in an -category.
And the definition of directed geometric realization of a quasi-category is evident. I have now added it to fundamental (infinity,1)-category. The directed geometric simplex we talked about before is the special case for .
Now one has to show that the canonical inclusion
is a Joyal weak equivalence, namely a weak equivalence on all hom-oo-groupoids. The proof of that would be the first half of the directed homotopy hypothesis which we want to get to work.
I don’t see any chance to get this to work with demanding the 2-cells in the directed to be paths of directed paths.
-
- CommentRowNumber23.
- CommentAuthorTim_Porter
- CommentTimeOct 1st 2010
My point is that the models should determine the theory rather than forcing an ’ugly sister’s foot’ into a beautiful glass slipper. :-)
When proper homotopy theory was first developed the theory one expected was not that which exactly fitted the models. Later on from another perspective it was found what adjustments made it fit, but that was later. Similarly my feeling is that your saying ” If there is going to be any good “directed homotopy theory” then directed paths need to be like morphisms in an (∞,1)-category”, is prejudging what the answer will be. A directed homotopy theory need not be a homotopy theory. In some cases it may be, but that would have to be proved, and the whole theory might influence what we think of as being a homotopy theory. (I will come back to this later on, but have to rush now.)
-
- CommentRowNumber24.
- CommentAuthorTim_Porter
- CommentTimeOct 1st 2010
Back again: I just looked at Marco’s book and he discusses a very rich homotopy theory based on d-spaces that uses a d-space structure on for a d-space, (around page 61 if anyone has a copy and is interested.) I am not sure what his theory translates to in -terms, but it has subtleties that are very pretty as well as some bits that are less so.
I wonder if directed space should really speak of d-spaces rather than directed spaces and if we might use 1-directed space as a synonym for d-space, that would leave us with working with higher order ’directed spaces’, where there were not only selected paths but selected (?) singular squares, cubes, etc.
Another thought is that we have a homotopy theory of directed spaces but could equally think of a ’directed homotopy theory of directed spaces’.
-
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeOct 1st 2010
- (edited Oct 1st 2010)
Similarly my feeling is that your saying “If there is going to be any good ’directed homotopy theory’ then directed paths need to be like morphisms in an (∞,1)-category”, is prejudging what the answer will be.
That’s true: it’s prejudging it to be the correct answer.
I hold these truths to be self-evident
that the right homotopy theory is Quillen’s on Kan complexes;
that the right directed homotopy theory is Joyal’s on weak Kan complexes.
I don’t see how we can but wander in the dark if we don’t take this seriously. In any case this is what i am after with directed spaces: formulate and prove the directed homotopy hypothesis for them, that identifies them with quasi-categories.
I just looked at Marco’s book and he discusses a very rich homotopy theory based on d-spaces
Homotopy theory in which sense? Does he provide a model category structure on d-spaces?
-
- CommentRowNumber26.
- CommentAuthorTim_Porter
- CommentTimeOct 1st 2010
Homotopy theory in his version of conditions on the structural homotopy data, so no mention of model categories as such.
I feel that you are pessimistic about the picture here. I do not think Marco, Martin Raussen, etc. feel they are wandering in the dark, rather they are exploring a new land, knowing full well the map of the undirected landscape.
Have you looked at Peter Bubenik’s papers? For instance, Peter Bubenik and Krzysztof Worytkiewicz. A model category structure for local po-spaces. Homology, Homotopy and Applications, 8 (2006), pp. 263-292. These may give you some linking ideas for a directed homotopy hypothesis. I do not have a good knowledge of their stuff but it probably needs looking at. (They may use your undirected homotopies I don’t know.) Peter has some other papers that may be of interest, including ones with statistical ideas being brought in to persistent homology and that is another situation in which evolving spaces occur. I must see if your ideas on quasi-cats could be likely to help in that area.
-
- CommentRowNumber27.
- CommentAuthorUrs
- CommentTimeOct 1st 2010
- (edited Oct 1st 2010)
I feel that you are pessimistic about the picture here
Maybe I am just not so interested in some of these concrete motivations from computer science etc. Instead, I observe that Joyal has given a definition of directed homotopy types in the combinatorial model, and that these support a rich theory that subsumes the classical combinatorial homotopy theory. So it is natural to ask for the geometric counterpart. That’s my motivation for directed spaces.
In contrast to that, you tell me that Grandis’ work on directed spaces has not led to any substantive results so far. It’s not so much that I am pessimistic about it’s future, I just observe that it’s present does not look so interesting, while Joyal’s model looks highly interesting.
Have you looked at Peter Bubenik’s papers? For instance, Peter Bubenik and Krzysztof Worytkiewicz. A model category structure for local po-spaces. Homology, Homotopy and Applications, 8 (2006), pp. 263-292. These may give you some linking ideas for a directed homotopy hypothesis
Thanks for the link. I just looked at it.
Let me see, here is my impression. Up to the last page they go through some standard observations, such as that the Jardine model structure exists and that given a model structure, we get one on the undercategory. The key definition for directed homotopy theory is def 8.8 on the second but last page. And i find it a bit curious. It effectively says that a directed homotopy equivalece is a map that becomes an ordinary homotopy equivalence after you invert all the directed paths! That’s a somwhat unexpected definition for directed homotopy theory! :-) (But maybe I am missing something. Let me know.)
Then the paper ends with saying
We claim that this model category provides a good model for studying concurrency. An analysis of this model category will be the subject of future research.
-
- CommentRowNumber28.
- CommentAuthorTim_Porter
- CommentTimeOct 1st 2010
- (edited Oct 1st 2010)
I think Marco makes real progress in suggesting new directions, for instance looking at cubical complexes as directed things. There are, as as one would expect, lots of results, but the main results relate to finding a suitable meaning for a minimal model of a fundamental category. I found those very nice indeed.
I think some of the riches and also some of the problems of directed homotopy theory as it stands at the moment, is that there are intuitions about what it might achieve, but no definite RESULTS, that say that it is getting there. ’Directed’ thereby means slightly different things to different workers in the field. (By RESULTS I mean BIG results!)
-
- CommentRowNumber29.
- CommentAuthorEric
- CommentTimeOct 1st 2010
I think there may be some semantic issue at play here. I’m not sure it is generally agreed upon that “directed space” should be synonymous (assuming some homotopy hypothesis) with -category. Is it?
If you forget the word “directed space”, I think I vaguely understand everything Urs says. You want a homotopy hypothesis for -categories. I can see why that is desirable. I’m just not sure I would call such a thing a “directed homotopy hypothesis”. I might call it a “semi-directed homotopy hypothesis” or something.
By the very nature of -categories (to the very limited extent I understand them), everything higher than dimension 1 is undirected, i.e. if it is invertible then I don’t consider it directed.
I would probably reserve the word “directed homotopy hypothesis” for that associated with -categories. Maybe even a subset of -categories whose morphisms are all directed/causal. The directed homotopy hypothesis should apply to directed -categories and it would probably reduce tension by renaming -categories to semi-directed spaces or something.
-
- CommentRowNumber30.
- CommentAuthorTim_Porter
- CommentTimeOct 1st 2010
@Eric That was more or less the feeling I was trying to express in that previous comment. I am coming from ’directed’ as distilled from examples including causality, processes, evolving spaces, persistent homology, pospaces, etc. (That process itself is fraught with confusion as to what is really appropriate.) Others are coming from other directions and the terminology does not always match.
I like your idea of differentiating the homotopy hypotheses. I suggest ’- homotopy hypothesis’ as the general one and then, Urs, your statement summarising Joyal is in the case . The filtration / indexation of these by may be useful, as it is a bit like building things in a Postnikov tower.
-
- CommentRowNumber31.
- CommentAuthorEric
- CommentTimeOct 1st 2010
- (edited Oct 1st 2010)
I like your idea of differentiating the homotopy hypotheses. I suggest ’- homotopy hypothesis’ as the general one and then, Urs, your statement summarising Joyal is in the case .
Cool. Yeah, but the doesn’t necessary deserve to be called “directed” either. We could have - homotopy hypotheses and also directed -homotopy hypotheses where directed is distinguished by the fact that all -morphisms for are directed.
Edit: A few 10s of minutes later…
This indicates that we should be able to speak of -spaces and -directed spaces where an -directed space is an -space where all -paths for are directed. However, I would move that the only -directed space that displays the “right spirit” would be , i.e. a “directed space” is an -directed space.
“Space” would then be synonymous with -directed space.
-
- CommentRowNumber32.
- CommentAuthorTim_Porter
- CommentTimeOct 1st 2010
- (edited Oct 1st 2010)
That would be my feeling, but there would be cases where there was truncation etc. That would be quite fun to look at. My experience with proper homotopy suggests there might be several different useful variants of homotopy ’groups’ and Marco Grandis’ ideas would seem to suggest the same thing. At any stage one can invert above any particular level and get a perhaps more calculable model of the same directed thing.
Sometimes there would only be sense in looking in low dimensions. For instance if we have an evolving space we have an evolving homotopy type. and if we are not worried about where a point at time t flows to at time t+1, say, then the can use simple models for the homotopy type and model the change by a 1-cell that is not invertible. My vague and perhaps silly picture is of a map and we watch the way in which the homotopy type of varies with . (You can imagine a contour height function, perhaps a Morse function on a manifold or whatever.)
-
- CommentRowNumber33.
- CommentAuthorMike Shulman
- CommentTimeOct 1st 2010
I don’t see any reason to believe that there is only one useful/interesting notion of “directed space” or “directed homotopy theory.” Certainly it makes sense to regard quasicategories as one sort of directed space and look for a notion of directed topological space with a homotopy theory that would be equivalent to it. But I see no reason to expect that all applications falling under the general heading of “directed homotopy theory” would use models that are equivalent to that one.
-
- CommentRowNumber34.
- CommentAuthorEric
- CommentTimeOct 2nd 2010
I don’t see any reason to believe that there is only one useful/interesting notion of “directed space” or “directed homotopy theory.
Yep yep. I agree. I didn’t mean to suggest otherwise. I think all the -directed spaces could be interesting and useful for various applications. My last comment was more about the “default” case. I was suggesting that when speaking of -directed spaces, the case most likely referred to colloquially as merely “directed space”, i.e. the default case, should probably be -directed spaces. Urs seems to want “directed space” to refer to the case, but that introduces a possible conflict with the way others think about it.
But what we consider “default” is not really important at all. How does the concept sound, i.e. specifying homotopy hypotheses by their position in , e.g. the -homotopy hypothesis? I like it (but my vote doesn’t count of course) :)
It might be good to refer to -spaces as “quasi-directed spaces” so the -homotopy hypothesis would relate quasi-categories to quasi-directed spaces. How does that sound?
-
- CommentRowNumber35.
- CommentAuthorTim_Porter
- CommentTimeOct 2nd 2010
I proposed that as an initial guideline a term such as 1-directed be applied to Marco’s d-spaces where selected paths are declared to be ’directed’, then 2-directed would mean 2-d-spaces with specified paths plus squares (with suitable axioms) being in the selection and so on. That terminology is perhaps not optimal but might work.
-
- CommentRowNumber36.
- CommentAuthorEric
- CommentTimeOct 2nd 2010
- (edited Oct 2nd 2010)
@Tim #35
That sounds like -directed and -directed spaces, which (similar to -categories) would be called 1-directed and 2-directed. It all seems consistent to me.
Edit: There is an interesting old discussion on this topic at (n,r)-category.
-
- CommentRowNumber37.
- CommentAuthorTim_Porter
- CommentTimeOct 2nd 2010
I’m not that enthralled to the terminology as there are things that are very useful but don’t quite fit into it. Am I right in thinking that a groupoid enriched category would be a (2,1)-category? (Sorry to ask such a simple question.)
-
- CommentRowNumber38.
- CommentAuthorTim_Porter
- CommentTimeOct 2nd 2010
On the page of the (n,r)-category I found
Even though they have no special name, (n,1)-categories are widely studied.
But track 2-categories, and groupoid enriched categories are often studied and track n-categories are n-cats with all n-cells invertible, so presumably are (n,n-1)-categories. Am I right? Hence (2,1)-categories are track 2-categories as used by Baues.
The hole in the terminology comes from having models that are weak n-categories but then seem strict above that! :-) Yes it is possible at least partially so. A 2-crossed complex corresponds to a Kan complex which has uniquely defined ’thin’ fillers above dimension 2 (I think), so is sort of strict there but in lower dimensions corresponds to a Gray-groupoid /2-crossed module. (I hope the idea is vaguely clear.)
-
- CommentRowNumber39.
- CommentAuthorMike Shulman
- CommentTimeOct 2nd 2010
There doesn’t seem much point to me in using (n,r) terminology for directed spaces, since an undirected space is already (∞,0); only the r needs to be notated. If you want to truncate to some n<∞, you could just say “r-directed homotopy n-type”.
I would also expect the “default” notion of “directed space” to be one in which paths are directed but not 2-paths. It’s not clear to me that there is a unique notion even here, though. Probably there is one notion of a “directed space equipped with a chosen skeleton” which is equivalent to a quasicategory, but it’s not obvious to me that that is the most natural notion of “directed space” for all other applications as well.
-
- CommentRowNumber40.
- CommentAuthorTim_Porter
- CommentTimeOct 3rd 2010
@Mike
Various points:
(i) The argument that 2-paths should be directed is based on an intuition in terms of rewriting or time. If we deform a 1-cell non-reversibly into another target one then we want to represent that deformation as a 2-cell, but the 2-cell should not then be invertible, as the second target 1-cell has, in some sense, been simplified from the first one.
(ii) The usual way in which a pospace leads to a ’directed space’ in fact leads to one in which 2-cells would be not necessarily reversible.
(iii) Any groupoid is a category, any ’track’ 2-category is a 2-category. Your default would be analogous to saying that the default for categories should be that they are groupoids!
(iv) I do not particularly like the term ’directed space’ because a directed set is not just a set with a partial order, but has a confluence condition. (Working with people in Lyon, they are using confluence in dimension n, and in that context, are also using (strict) n-categories in which the last direction is invertible but not necessarily the earlier ones.) Higher dimensional confluence is very interesting but nowhere in the realm of our discussions are we introducing ’directed’ with that sort of sense.
-
- CommentRowNumber41.
- CommentAuthorUrs
- CommentTimeOct 3rd 2010
- (edited Oct 3rd 2010)
I don’t see any reason to believe that there is only one useful/interesting notion of “directed space” or “directed homotopy theory.”
Time will tell.
Recall where this discussion originated in, around #18. The well understood combinatorial part of 1-directed spaces serves at least to show that it is a good idea to have a defininition of fundamental -category where the 2-cells are not paths of directed paths.
That’s because there is an evident notion of “directed geometric realization” of a quasi-category. This is certainly a canonical example of a class of directed spaces. And to recover the original -category from its directed geometric realization, one must not impose these paths of directed paths.
I think my point is: we have a huge amount of information about the combinatorial side of the 1-directed homotopy hypothesis. It seems natural to build on that, while it seems less natural to invest lots of energy into alternative approaches that don’t have much of a guiding principle.
My point is not that such alternative approaches won’t eventually exist and be useful. But that we’ll be in the dark about them without further guidance or results.
So when somebody says that a fundamental -category certainly must have paths of directed paths as its 2-cells, I point out that, no, on the contrary, in the only approach about which we do have substantial insight, this is wrong.
-
- CommentRowNumber42.
- CommentAuthorEric
- CommentTimeOct 3rd 2010
- (edited Oct 3rd 2010)
Note: This comment was in response to Tim’s comment #40 above.
I’m guessing the tendency to want 1-paths directed and 2-paths undirected has to do with “bigon thinking” (which is potentially biased in my opinion).
If your source and target 1-paths share the same start and end points, then the 2-path connecting them CANNOT be directed. It is causally impossible. The source 1-path cannot evolve into the target 1-path. So bigons are not in the “right spirit” of directed spaces.
If you think of a directed space conceptually as a river with island barriers and branches forcing you to move around them, then a directed 1-path would be the course traced out by a tiny boat that could only move sideways (transverse to the flow) as it floats downstream. It must always “move forward”, but can shift left or right (assuming downstream is “up” like the old video games).
Now, tie a bunch of tiny boats together. A directed 2-path would be the surface traced out by the tiny boats as they tried steering around.
This causal shape is quite different in spirit than a bigon.
-
- CommentRowNumber43.
- CommentAuthorTim_Porter
- CommentTimeOct 3rd 2010
I think that we are, as sometimes happens, talking at crossed purposes. I do not think we are in the dark about the more general gadgets. For instance, Marco puts forward cubical sets as one example of his theory, yet is taking the directed n-cube in the usual sense. He talks about geometric realisation as a d-space. BUT the directed n-cube is also possible to view as a higher dimensionally directed cell, so with very little extra work I think one would have a n-category type version with n-cells not necessarily invertible (and that is the point NOT NECESSARILY. They may be but need not be.)
The Grandis form of d-space comes with a forget functor to spaces. This has left and right adjoints. The left one says the only distinguished paths are constant, the right one says all paths are distinguished. In general what I am saying is that we have to take things in between as well.
If the model is to have directed geometric content then deformations / 2-cells should be paths in the space of directed paths without that assumption directed geometric content goes by the board. The point you make still is useful, since there would be a morphism of some sort to a well understood object but the object that one really needs to study is sitting over it.
Although I do not subscribe wholeheartedly to Marco’s picture of things, I think his results show that there is a lot of useful categorical machinery that can be brought to bear on the problem and in the generality that you seem to want to avoid.
-
- CommentRowNumber44.
- CommentAuthorEric
- CommentTimeOct 3rd 2010
So when somebody says that a fundamental -category certainly must have paths of directed paths as its 2-cells
I don’t think anyone would say this (on purpose).
If someone poses the question “Should the fundamental -category of an -space contain directed 2-paths of directed 1-paths?” I think the answer is obviously, “No”. All 2-paths would be invertible (unless I’m horribly confused) and hence cannot be directed.
If someone poses the question “Should the fundamental category of a directed space contain directed 2-paths of directed 1-paths?” I think the answer would be, “That depends on how you define ’directed space’”.
I think you have already taken it as a given definition that a directed space is an space, which is creating some confusion among people who think about directed spaces. That would take some convincing, but is conceivable. I’d be willing to recalibrate if shown the errors of my ways.
I think a decent name for an -space would be “quasi-directed space”. Then, as I’ve said above, the homotopy hypothesis you are after would relate quasi-categories and quasi-directed spaces.
To deserve the word “space”, I think you need . Then -space is just a space, -space is a quasi-directed space, and an -space (or just -space) would be a directed space.
-
- CommentRowNumber45.
- CommentAuthorTim_Porter
- CommentTimeOct 3rd 2010
In all this, with a shape theorists hat on, I feel that a directed space should be a space, plus structure, such as a local order. I have never liked the tendency amongst some topologists of calling and simplicial set ‘a space’. This is the same problem as here.
Imagine some space with a sense of flow, or with a sense of being evolving (each point having a time counter, but time could be branching). There would be objects = points, 1-cells being paths consistent with the time counter, and a useful notion would be to deform one such path to another through intermediate similar paths. (I suspect some fibred categorical model might eventually be useful here, say over a locale, but for today, I will stick with a topological picture.) There would, for instance, be the possibility that two different paths, which were not linked by any such deformation could be deformed into a third one, a sort of confluence situation. (The third path was in the ’possible future cone’ of both of the first two.) We would not want to consider the two original paths to be directly linked by a 2-cell, although they would be by a zig-zag of 2-cells. We would have a 2-category( after a bit more fiddling around and dividing out by suitable 2-homotopies). I do not see that this situation is that strange, and should be able to be subsummed under a notion of model for the directed homotopy of a ’directed space’. It may not be a -category, … bad luck, it is there and needs studying as a situation modelling an interesting segment of directed homotopy. (Directed homotopy theory may be an ugly sister’s foot that does not fit well into the immediately available (glass slipper) models but will be related to them.) Proper homotopy theory does not fit that neatly into the quasi-cat framework but still has rich structure that mirrors quite well the geometry of non-compact manifolds. Similar points hold to strong shape theory. They are very manageable and give us good information. They also have very clear n-cat interpretations and historically led to some of the models for weak infinity categories (look at Batanin’s work). I am not that pessimistic about the notion of directed homotopy. I think it leads to some interesting problems.
(And I know that glass slipper was probably a mistranslation from the French, so we don’t need to discuss that here!:-))
Getting away from that discussion slightly, Marco has some nice things to say about future invariance and past invariance. He tries to see how the directed homotopy of the future changes along a directed path, and to use this to thin down the fundamental category of a d-space to something smaller. This looks good and I may try and explain it (once I understand it better).
-
- CommentRowNumber46.
- CommentAuthorEric
- CommentTimeOct 3rd 2010
- (edited Oct 3rd 2010)
Note: Posted before seeing Tim’s previous cool comment.
Here is an example…
Let’s say that the direction of our directed space is “up” and we have two impenetrable islands as depicted below.
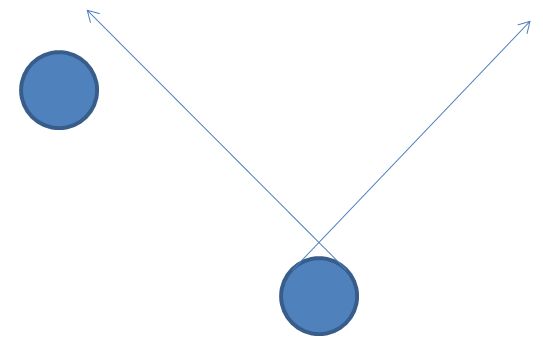
Note: The arrows depicts the maximum speed a boat can travel around the bottom island. Similar to a light cone.
The upper left island is too far away from the bottom right arrow so that any “boat” that passes on the right of the first island cannot get around to the left of the left island.
How would the fundamental categories differ depending on what types of 2-paths are allowed? Would they be identical?
-
- CommentRowNumber47.
- CommentAuthorUrs
- CommentTimeOct 3rd 2010
Tim says:
puts forward cubical sets as one example of his theory
But nobody has a model for directed homotopy types (aka -categories) in terms of cubical sets.
Eric says
I don’t think anyone would say [that 2-cells should run through directed paths] (on purpose).
David R. said this in #18 in this thread. Mike made a remark to that extent in #5 in the parallel thread “fundamental -category”
My emphasis here on the fact that we should be looking at the directed homotopy theory which does exists – namely Joyal’s – is to point out that in that context it is clearly not the right thing to demand.
This is part of what I mean by “being in the dark”. If we want to find a good model of directed spaces and fundamental -categories, we should check against existing results, not just against our intuition. Our intuition may be wrong.
-
- CommentRowNumber48.
- CommentAuthorTim_Porter
- CommentTimeOct 3rd 2010
@Urs I must say that the most developed directed homotopy theory is not only André’s. (Although I have NOT seen this.) The views of Martin Raussen, Lizbeth Fajstrupp, Marco, Eric Goubault, and Philippe Gaucher (and others) also need noting. That is a considerable body of hard mathematics related to the general notion of directed algebraic topology. As a ’devil’s advocate’ let me say that even if the theory put forward by André was beautiful, (and most surely it will be) the need of the applications AND very natural situations that occur in mathematics might say that there was no actual use for that theory in this area as it did not fit the situations of interest.
My point is to go beyond yours and say : Suppose we go for the more general model, then we can for calculations, escape down to something weaker, such as André’s and use this to find invariants, etc. Once that is done we have an obstruction / lifting/ rectification problem somewhat similar to that when we lift back up from chain complexes to crossed complexes and then beyond that to quadratic complexes. We might not expect all models in Joyal’s sense to lift to non-trivial models in the next level up (2-directed ones), the obstructions would then tell us a lot of information about the situation being modelled. Likewise there would be ‘Joyal models’ that would lift non-uniquely to 2-directed models and again that gives a classification problem. (Passing from 2-directed to 1-directed might be analogous to localising.)
Another idea is that a useful model for some directed spatial phenomena may be presheaves (or perhaps homotopy coherent presheaves) of quasi-categories. Think of this as indexed homotopy theory. I do not necessarily mean the base is spatial or that it represents time. It represents a ’parameter space’ and could be almost anything. Would that provide a model for the situations that Eric and I hope to model, and what would the resulting theory look like.
-
- CommentRowNumber49.
- CommentAuthorUrs
- CommentTimeOct 3rd 2010
- (edited Oct 3rd 2010)
not only André’s. (Although I have NOT seen this.)
You have: as I said, I am talking about quasi-categories. We know that these are a good directed analog of ordinary homotopy theory.
We know three items in this table very well
So the evident question is what fills this table in the bottom right corner? Whatever it is, that deserves to be called a topological model for directed homotopy theory.
The views of Martin Raussen, Lizbeth Fajstrupp, Marco, Eric Goubault, and Philippe Gaucher (and others) also need noting. That is a considerable body of hard mathematics related to the general notion of directed algebraic topology.
Okay. I am likely ignorant of most of this. Could you summarize some highlights?
let me say that even if the theory put forward by André was beautiful, (and most surely it will be) the need of the applications AND very natural situations that occur in mathematics might say that there was no actual use for that theory in this area as it did not fit the situations of interest.
So maybe the situations of interest that you do mean are not actually that much “homotopy theoretically”? For I find it hard to see how one can argue that quasi-categories have not proven to be the right tool for studying examples in directed homotopy theory.
Another idea is that a useful model for some directed spatial phenomena may be presheaves (or perhaps homotopy coherent presheaves) of quasi-categories.
That’s the next step. -topos theory modeled by presheaves of directed spaces.
-
- CommentRowNumber50.
- CommentAuthorTim_Porter
- CommentTimeOct 3rd 2010
Sorry but I do not see quasi categories as being about directed homotopy theory. They are more important than that!:-) They do provideinsights, but I am a bit allergic to the idea of ‘ ’right tool’, and what examples of directed homotopy theory are you thinking of.
In fact although I worked on quasi categories back in the 1980s I have not really read André or Lurie in detail, although I do have a generally good idea of what they have done.
-
- CommentRowNumber51.
- CommentAuthorEric
- CommentTimeOct 3rd 2010
- (edited Oct 3rd 2010)
@Urs #47
Eric says
I don’t think anyone would say [that 2-cells should run through directed paths] (on purpose).
David R. said this in #18 in this thread. Mike made a remark to that extent in #5 in the parallel thread “fundamental -category”
Actually, I think it is fine (but what do I know?!) to want 2-paths to pass through directed 1-paths. Sorry about that. What I meant was that when talking about -stuff then you shouldn’t expect this to be done in a directed way, i.e. the 2-paths passing through directed 1-paths are themselves undirected because they are invertible.
If you want to allow 2-paths between undirected 1-paths, then what would your fundamental category for my diagram above look like? I think it would be different than the fundamental category when 2-paths are restricted to pass between directed. a.k.a. causal, 1-paths.
I think (but am likely wrong) that if 2-paths only pass through directed 1-paths, then the fundamental category in my example will consist of just three equivalence class of paths illustrated below.
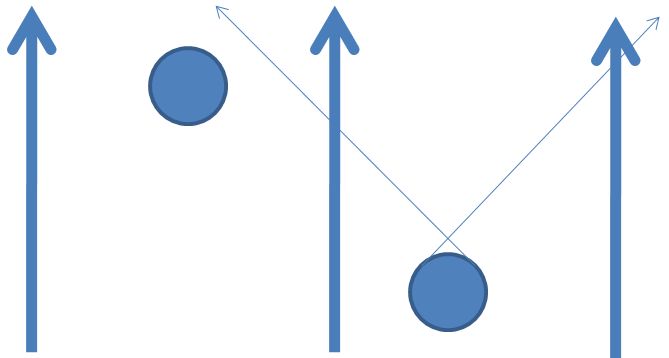
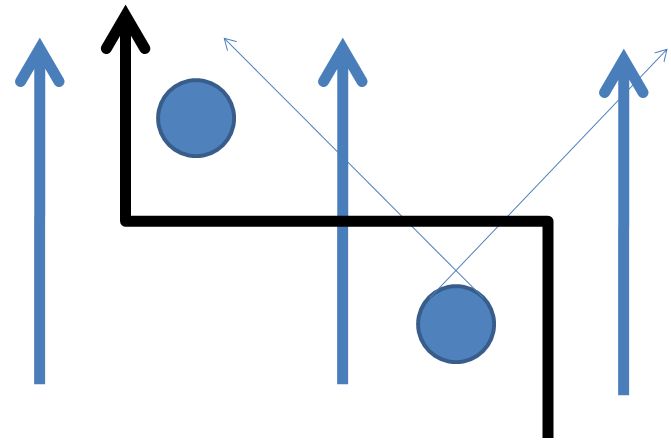
However, if 2-paths are not restricted to passing through directed 1-paths, then we pick up an addition equivalence class of paths illustrated below that would not be allowed if things were causal.
I’m probably just completely confused. How do things work in this trivial example?
Note: DIRECTED ALGEBRAIC TOPOLOGY, CATEGORIES AND HIGHER CATEGORIES
-
- CommentRowNumber52.
- CommentAuthorTim_Porter
- CommentTimeOct 3rd 2010
I’m afraid I do not understand your calculation. The paths should all be feasible and the black one isn’t. I understand what your trying to produce, but I’m not sure that this example gives it. My understanding of the fundamental category would be to have all points as objects and then (?) homotopy classes of directed paths between them. Is the question whether (?) should be ’directed’ or not? I will have to think a bit. (doh)
-
- CommentRowNumber53.
- CommentAuthorUrs
- CommentTimeOct 3rd 2010
- (edited Oct 3rd 2010)
Sorry but I do not see quasi categories as being about directed homotopy theory.
Do you agree that Kan complexes provide a combinatorial model for ordinary homotopy theory?
-
- CommentRowNumber54.
- CommentAuthorTim_Porter
- CommentTimeOct 3rd 2010
No. But before you dispair of me, they provide a combinatorial model of ordinary homotopy types. I believe that quasi categories, as they generalise categories, do provide a good combinatorial model for 1-directed homotopy types, i.e., in which the way in which directed 1-cells deform seems to be undirected. Quasi-categories are about ordinary homotopy theory as well as, of course, comparisons of homotopy types are not necessarily invertible. That gives a locally Kan simplicially enriched category and hence a quasicategory (as you know well).
I do not think that it is wise to stop there, as there are probably cases of (perhaps local) pospaces that have a difference in higher directedness and the assumption that 2-cells need not be directed would not seem to make sense there. I think that homotopy of dipaths and dihomotopy of dipaths both work, are related, and, probably the former is easier to calculate with than the latter. These both assume that the homotopy passes through dipaths, since from the theory there are no other maps around. (In my paper, I did not investigate whether the simplicially enriched categories that result are Kan enriched, or quasi-cat enriched or not at all, something that would have been useful.)
-
- CommentRowNumber55.
- CommentAuthorUrs
- CommentTimeOct 3rd 2010
- (edited Oct 3rd 2010)
No.
Then it’s not wonder that we cannot agree! ;-)
they provide a combinatorial model of ordinary homotopy types.
That’s what the homotopy 1-category of Kan complexes knows about. But the full Kan-complex enriched category of all Kan complexes does much more. It knows the full homotopy theory.
I believe that quasi categories, as they generalise categories, do provide a good combinatorial model for 1-directed homotopy types,
So maybe we can find agreement after all!
I do not think that it is wise to stop there, as there are probably cases of (perhaps local) pospaces that have a difference in higher directedness and the assumption that 2-cells need not be directed would not seem to make sense there
Sure, but that’s then talking about 2-directed spaces, 3-directed spaces, etc.
Is that maybe the whole disagreement that you thought I meant by “directed homotopy theory” the -directed version for all , whereas what I did mean was the 1-directed version?
I suggest: let’s get the 1-directed homotopy hypothesis under control first. Once we understand that, we can think about higher directedness. Experience from the combinatorial side suggests that after 1 it will get much harder.
-
- CommentRowNumber56.
- CommentAuthorTim_Porter
- CommentTimeOct 3rd 2010
I agree!
No I did not think you meant that I felt that without an index the term should be kept for the general case and not ’purloined’ for use of what may be 1-directed. (We should not rush into calling it that but it will do as an interim term at least.)
I can see some hope in higher dimensions but it is vaguer.
-
- CommentRowNumber57.
- CommentAuthorMike Shulman
- CommentTimeOct 4th 2010
I don’t have time to follow this whole discussion, but re: whether 2-paths between directed paths should pass through only directed paths, consider the 2-disc made into a directed space in such a way that there are exactly two directed paths (up to reparametrization) from (-1,0) to (1,0): one going clockwise around the top and one going counterclockwise around the bottom. These two paths give rise to two 1-morphisms in the fundamental (whatever)-category; are these two 1-morphisms equivalent? If 2-paths between directed paths can pass through undirected paths, then yes, they are: the disc itself provides a homotopy. But that is greatly against my intuition for what it means to call this a “directed space.” Maybe there are different notions of directed space; which is/are useful? That should be the question.
Yes, quasicategories are undoubtedly useful. But I think it is not valid to call them “a notion of directed space” until we have a prior notion of directed space and have proven them equivalent to it. The only reason it’s at all sensible to call Kan complexes “a notion of space” is because of the truth of the homotopy hypothesis; the implication doesn’t go the other way.
-
- CommentRowNumber58.
- CommentAuthorUrs
- CommentTimeOct 4th 2010
The only reason it’s at all sensible to call Kan complexes “a notion of space” is because of the truth of the homotopy hypothesis; the implication doesn’t go the other way.
Right. But once it is true, we have that a quasi-category is evidently a Kan complex with directed edges.
Concernign your disk-example: I find it very useful to buld intuition from the directed geometric realizations of quasi-categories: the ordinary geom realization with directed paths the order preserving maps through the 1-skeleton start start and end at vertices. in that pciture one sees that your disk example should be regarded as producing two equivalent 1-paths.
-
- CommentRowNumber59.
- CommentAuthorEric
- CommentTimeOct 4th 2010
- (edited Oct 4th 2010)
Regarding my diagrams in #51, Tim said in #52:
I’m afraid I do not understand your calculation. The paths should all be feasible and the black one isn’t. I understand what your trying to produce, but I’m not sure that this example gives it. My understanding of the fundamental category would be to have all points as objects and then (?) homotopy classes of directed paths between them. Is the question whether (?) should be ’directed’ or not? I will have to think a bit. (doh)
If it helps, we should think of all my arrows as originating from the same point in the “distant past” and recombining at the same point in the “distant future”.
It is clear that if the allowed 2-paths only pass through directed 1-paths, then the black path is not allowed. However, maybe I’m just confused, it seems that if 2-paths are not constrained to pass through directed 1-paths, then the black path is allowed. Is the black path allowed, i.e. is it part of the fundamental category, in what Urs is talking about?
-
- CommentRowNumber60.
- CommentAuthorMike Shulman
- CommentTimeOct 4th 2010
A quasicategory is evidently a Kan complex with directed edges, but that does not necessarily mean that it is the same as a directed space. The whole point I’m making is that it’s not clear that directed geometric realizations of quasicategories are the right way to build intuition for directed spaces.
-
- CommentRowNumber61.
- CommentAuthorTim_Porter
- CommentTimeOct 4th 2010
@Eric Terminology : I think of the fundmental groupoid as being on all points of the space and then one can hope to find a nice cuddly model on a few selected base points that is equivalent. Similalry the fundamental category here has all points in the space as its objects and then one looks for a nice model. (Marco discusses the problem of what nice in a full chapter so I won’t try to here.) You are talking about the hom category within that from to . Next a path is selected in your d-space if it is increasing (going up the page) and makes an angle of between 45 and 135 degrees to the positive x-axis.. (right?). Then I agree has three elements, the three blue arrows. The black arrow does not exist. Any d-path between the points is d-homotopic to one of the three. Perhaps I have misunderstood your blue discs. If you interpret them as being as in Mike’s example then something interesting happens. To be more precise, make them not solid islands but ’no go areas’ ’shallows’, ’whirlpools’ or whatever imagery tickles your fancy, then no directed path in the plane can pass through them. The black paths is still not there but whilst dihomotopies still give the same answer, perhaps, (and this is debatable) allowing homotopies to use paths that DO pass through them makes the three elements collapse to just one.
@Mike Marco introduced d-spaces as a neat setting to do something he called directed homotopy theory. The choice was because it has nice categorical properties AND contains lots of examples relating to the concrete situations in which directed homotopy was being applied (pospaces etc.) dTop has exponentiable objects so one can form a d-spaces of d-paths in a d-space, and d-homotopy corresponds to paths in that. I am not 100% convinced by d-spaces because of the sort of example that you mention, but their theory works very nicely and is quite pretty.
One form of a directed homotopy hypothesis would be to find a geometric realisation from some nice category of weak infinity cats back to dTop, which gave an equivalence of homotopy categories in some shape. That is not the version that Urs mentions of course. His woud be interesting as well as it would give additional tools for quasi-cats.
Must rush. I should be writing a report on a paper, and then have to go to the Dentists! :-)
-
- CommentRowNumber62.
- CommentAuthorEric
- CommentTimeOct 4th 2010
- (edited Oct 4th 2010)
@Tim #61: My visual aid was “boats in a river” so an “impenetrable island” is definitely a “no go” area :) The intention of the blue disk is that no 1-path can pass through it and no 2-path can pass across it.
-
- CommentRowNumber63.
- CommentAuthorTim_Porter
- CommentTimeOct 4th 2010
’Nothing’? do you mean really nothing or nothing directed? I understood what you said but not precisely, i.e. in directed land the black path just does not exist, but neither is it reachable from one of the blue arrow by a homotopy (<-not directed). (And I would not like to drive a boat through shallows or across a whirlpool either. :-))
-
- CommentRowNumber64.
- CommentAuthorUrs
- CommentTimeOct 4th 2010
Mike,
sure, one will have to formulate and prove the directed homotopy hypothesis, in order to be sure. I am talking about this in the parallel thread.
I haven’t proven it yet, but it looks very plausible to me that the directed geometric realization and the definition of fundamental (oo,1)-category that I gave should work. In any case, the directed geometric realization is a plausible geometric incarnation of quasi-categories, and as such it does shed light on questions like in your disk example. It provides a background framework against which to test intuition about that disk-example, I think.
In the parallel thread I sketch what one still needs to prove to get the directed homotopy hypothesis. I looks like it might actually be an easy proof, using the standard homotopy hypothesis, but I don’t have it yet.
-
- CommentRowNumber65.
- CommentAuthorTim_Porter
- CommentTimeOct 4th 2010
Can I suggest ’(1-)directed homotopy hypothesis’ be used otherwise the same confusion will reign as before!
-
- CommentRowNumber66.
- CommentAuthorEric
- CommentTimeOct 4th 2010
And until the connection to existing notions of “directed spaces” is better established, I would recommend using “quasi-directed space” to describe the other side of the -homotopy hypothesis coin opposite quasi-categories.
-
- CommentRowNumber67.
- CommentAuthorUrs
- CommentTimeOct 4th 2010
Eric,
as was pointed out before, it does not make sense to keep the ““-around when talking about homotopy-theoretical things. That’s implicit.
-
- CommentRowNumber68.
- CommentAuthorEric
- CommentTimeOct 4th 2010
- (edited Oct 4th 2010)
as was pointed out before, it does not make sense to keep the ““-around when talking about homotopy-theoretical things. That’s implicit.
I think I understand this, but there is no harm I can see in keeping it explicit. Ultimately, I “think” there might be a difference between “1-directed” (being short for -directed) and -directed, which I’d still like to call “quasi-directed”. Getting the terminology right from the beginning could avoid some clashes down the road.
Has anyone ever studied “(abstract) finitary homotopy” where we have an abstract interval rather than a continuum interval? I can imagine cases where you might have a large abstract complex with subcomplexes connected by abstract edges (and higher cells) that can be interpreted as (abstract) finitary homotopies. In this finitary environment it would seem that you could have -homotopy hypothesis for finite (even if it isn’t very exciting). After all, homotopy is about sliding spaces around and this can be done abstractly without a continuum interval.
The implies a continuum.
Note to self (and anyone else interested):
-
- CommentRowNumber69.
- CommentAuthorUrs
- CommentTimeOct 4th 2010
Has anyone ever studied “(abstract) finitary homotopy” where we have an abstract interval rather than a continuum interval?
Yes, that’s the homotopy theory modeled by Kan complexes. The role of the interval is played by the interval groupoid.
The (∞,−) implies a continuum.
No, it doesn’t It’s the geometric version of homotopy theory in terms of topological spaces that does. The combinatorial version in terms of simplicial sets and Kan complexes does not.
-
- CommentRowNumber70.
- CommentAuthorTim_Porter
- CommentTimeOct 4th 2010
There are very nice results by Jonathan Barmak (Buenos Aires) on finite spaces. They are well worth looking at. Eric’s link to Peter May’s webpage on finite topological spaces has links to his papers with Gabriel Minian.
-
- CommentRowNumber71.
- CommentAuthorTim_Porter
- CommentTimeOct 4th 2010
Finite spaces are great fun to work with. and when I have written the 100 or so pages for the n-Lab that I have more or less promised to do, I might write some more on that subject. They are also very useful. Note the result of McCord from way back, that finite topological spaces model ALL homotopy types of compact simplicial complexes and therefore an Awesome part of homotopy theory. Barmak’s work (for his PhD thesis!) pushed things a lot further and peter May seems to think very highly of that work, so this is an area to watch.
-
- CommentRowNumber72.
- CommentAuthorEric
- CommentTimeOct 4th 2010
- (edited Oct 4th 2010)
Barmak’s work (for his PhD thesis!) pushed things a lot further and peter May seems to think very highly of that work, so this is an area to watch.
Yeah. I was happily surprised to see so many recent references.
When I was in grad school, I independently rediscovered (although it is pretty obvious I guess) that you can get interesting finite topological models of continuum spaces in exactly the way outlined in some of those papers. The thing I thought was interesting is that any such model must necessarily be non-Hausdorff. That is why I throw in a “(non-Hausdorff)” whenever I mention it. This means that any finitary model of the physical universe (modest proposal) must necessarily be non-Hausdorff. This would likely wreak some havoc with some popular “no go” theorems. Hausdorff spaces are pretty deeply ingrained in the minds of most physicists.
In my dissertation, I wrote:
When it comes to constructing continuum models of space-time, the proposition that distinct events are in fact separated is usually seen as a reasonable requirement. Hence, the underlying topological spaces on top of which continuum models of space-time are to be built are usually assumed to be Hausdorff.
[snip]
- Assuming space-time to be Hausdorff is convenient, but is by no means necessary.
Note the result of McCord from way back
I LOVE that “old school” algebraic topology stuff. My all time favorite mathematician is Whitney. I treasure my copy of Lefschetz.
I wonder what those guys would think of this n-Stuff?
-
- CommentRowNumber73.
- CommentAuthorMike Shulman
- CommentTimeOct 4th 2010
If you want a notion of directed space to give you intuitions about quasicategories, that’s great. I’m just saying there may be other inequivalent notions of directed space. In particular, the notion of directed space you’re working with in the other thread has the property that a sub-path of a directed path is not in general directed, nor is a constant path in general directed. Something like this seems to be necessary if you want an equivalence with quasicategories, but it is not part of my a priori intuition about what a directed space should be (nor, I believe, is it part of Grandis’ d-spaces).
-
- CommentRowNumber74.
- CommentAuthorEric
- CommentTimeOct 5th 2010
a sub-path of a directed path is not in general directed
Would this occur in only extreme pathological cases, or is it a general feature of this approach?
Would the same ever happen in Grandis’ approach?
-
- CommentRowNumber75.
- CommentAuthorTim_Porter
- CommentTimeOct 5th 2010
- (edited Oct 5th 2010)
Marco (p. 51 of his book and in his papers) does not require subpaths of d-paths to be d-paths. The d-space structure is given exactly as in directed topological space. As this is an abstract structure, you can try to tweek an example for which a subpath ’closure’ axiom does hold and delete one subtah that does not seem to matter, so one can make it pathological. Mike’s example of the directed circle could be made into one which was subpath closed, I think, but and that would change the fundamental category as we would then have the set of ’objects’ would include all points on the boundary of the disc.
In your river example, you looked at d-paths from -infinity to infinity and just at that part of the fundamental category, but there would be fun going on on the boundaries of the circular islands as well. Suppose you take a point on one those which has a tangent line which has too shallow a gradient (i.e. less than 45 degs), I don’t think the ’boat’ could escape! Fun. It is something like a deadlock in the Swiss flag example, but there is no ’hole’ into which the path is disappearing. (Am I right?) That example and similar ones should be looked at in a LOT of detail.
-
- CommentRowNumber76.
- CommentAuthorMike Shulman
- CommentTimeOct 5th 2010
I read part (2) of the definition here as implying closure under “subpaths” in a suitable sense. E.g. if is directed and , then choose the natural increasing homeomeorphism and compose it with the inclusion to show that the “subpath from a to b” of any directed path is also directed. The definition part (1) also explicitly includes all constant paths as directed. (These are both differences from the definition given at fundamental (infinity,1)-category, which only allows reparamatrization by homeomorphisms and does not include constant maps.) Therefore, the object-set of the fundamental category must be the set of all points of the space. Unless I’m reading something wrong somewhere?
-
- CommentRowNumber77.
- CommentAuthorTim_Porter
- CommentTimeOct 5th 2010
You are right. That point had escaped me as I was thinking of reparametrisation whilst Marco talks of ’partial reparametrisation’. The object set must be all the points because the constant paths are selected. It is worth noting, as I have mentioned before, that Marco puts a lot of effort (Chapter 3, pp145-226) into modelling the fundamental category. By this he means that he is seeking small models (representative objects and arrows) that encode enough of the structure. Equivalence is not the question here as that destroys too much of the structure. In reading the book, this struck me as being the most immediately important chapter. I should offer to summarise it, and will have to write a review of the book shortly, but I cannot do so just now.
-
- CommentRowNumber78.
- CommentAuthorUrs
- CommentTimeOct 5th 2010
- (edited Oct 5th 2010)
If you want a notion of directed space to give you intuitions about quasicategories, that’s great.
No, the other way round: I want to use quasi-categories to give me intuition for what a notion of directed space can be that has a chance of supporting a directed homotopy hypothesis.
For I think that it is clear that quasi-categories are one side of the directed homotopy hypothesis, so we can use them to deduce what the other side can be and what not.
I’m just saying there may be other inequivalent notions of directed space. In particular, the notion of directed space you’re working with in the other thread has the property that a sub-path of a directed path is not in general directed, nor is a constant path in general directed. Something like this seems to be necessary if you want an equivalence with quasicategories, but it is not part of my a priori intuition about what a directed space should be (nor, I believe, is it part of Grandis’ d-spaces).
Yes, so for the purposes of actually doing directed homotopy theory I find it hard to see how other definitions would do the trick. Of course there may be many sensible definitions of directed topology . But that’s a big difference to directed homotopy theory.
-
- CommentRowNumber79.
- CommentAuthorMike Shulman
- CommentTimeOct 6th 2010
Urs, it seems to me that you have a very blinkered view of what “directed homotopy theory” might mean. It sounds to me as though it should encompass the homotopy theory of directed spaces, for whatever notion(s) of directed space turn out to be useful. One notion of directed space may turn out to have a homotopy theory that is equivalent to quasicategories, but another may not, and yet it would still be a homotopy theory that (to my mind) merits inclusion under the term “directed homotopy theory”.
-
- CommentRowNumber80.
- CommentAuthorMike Shulman
- CommentTimeOct 6th 2010
In particular, Grandis’ book is called “Directed Homotopy Theory,” but as I pointed out above, his notion of directed space is not likely to be equivalent to quasicategories. I think we should let the people who’ve been studying “directed homotopy theory” all this time have some say in what the term means. (-:
-
- CommentRowNumber81.
- CommentAuthorDavidRoberts
- CommentTimeOct 6th 2010
One thing which may be worth considering is that for each directed space structure D on the geometric n-simplex you’ll get a different notion of fundamental oo,1-category, subject to the requirement that the standard retracts behave well with respect to D. For example, I was thinking of perhaps having a codimension one foliation on the n-simplex and directed paths are deemed to be those transverse to the leaves. This statement is a bit rubbery, because one has to take care of boundaries and corners, and we may have to restrict to PL- or piecewise-smooth paths
-
- CommentRowNumber82.
- CommentAuthorEric
- CommentTimeOct 6th 2010
In particular, Grandis’ book is called “Directed Homotopy Theory,” but as I pointed out above, his notion of directed space is not likely to be equivalent to quasicategories. I think we should let the people who’ve been studying “directed homotopy theory” all this time have some say in what the term means. (-:
Yes yes. Please Urs, if possible could you try to avoid the naming conflict here and call your stuff (as important and useful as it may be) something else? I’ve proposed “quasi-directed” for what you’re doing, but the name doesn’t matter AS LONG AS you don’t call it “directed”. I think the stuff Grandis is working on deserves priority for that adjective.
-
- CommentRowNumber83.
- CommentAuthorUrs
- CommentTimeOct 6th 2010
- (edited Oct 6th 2010)
Urs, it seems to me that you have a very blinkered view of what “directed homotopy theory” might mean.
That’s right! I think homotopy theory is such an important concept that it would be good to be very restrictive about what to call any supposed generalization.
I think we should let the people who’ve been studying “directed homotopy theory” all this time have some say in what the term means. (-:
Sure, but this is turning the way the discussion came about on its head now: I am not trying to make all people adhere to some notion (I would if I had more time and energy! ;-). No, what happened here was conversely that I found that discussion of existing notions of “directed homotopy theory” were clearly missing some aspect, because quasi-categories did not fit in, so I started to suggest that whatever directed spaces are taken to be, one canonical class examples must come from quasi-categories, and there must be a notion of fundamental -category recovering this and we must not dismiss notions of directed spaces and fundamental -category that achieve this.
In short, a notion of directed homotopy theory maybe does not have to be restricted to one corresponding to quasi-categories, but if it does not at least include it, it is clearly missing something.
I said this before, but I say it again: there is a difference between topology and homotopy theory. Much of what motivates existing work on “directed homotopy theory” to me seems to be more like directed topology .
But I don’t want to fight about terminology. What I want is to highlight that there is a glaring open problem in directed homotopy theory (by whatever interpretation of the term): find the notion of directed space that proves a directed homotopy hypothesis with quasi-categories on one side. And that looking at this glaring open problem does adjust some intuitions about what directed spaces should obviously be like. I think it is important to think about this.
-
- CommentRowNumber84.
- CommentAuthorDavidRoberts
- CommentTimeOct 6th 2010
I certainly accept Urs approach. I just would like to see if there is a way to get a fundamental (oo,1)-category structure from different directed space structures on . My inspiration comes from thinking of the nerves of various ’crossed beasties’, whereby the definition of the fundamental ’crossed beastie’ of the n-simplex determined it for all the rest.
There is certainly a directed space structure on where the interior points are in the image of a directed path: If one imagines as being the triangle with base the interval , then directed paths are those with increasing first coordinate. Then more generally (and I’m starting to think aloud here), take a model of the n-simplex affinely embedded in (using only the first coordinates) whereby the induced path given by restricting to the spine is monotonically increasing in its first coordinate. Then any path in the 1-skeleton such that the order of the vertices is always increasing has increasing first coordinate. Now define a path in to be directed if the path is increasing. This captures Urs’ notion of directed path.
Then there is a homotopy inside the 2-skeleton fixing the endpoints between order-preserving paths, such that this homotopy is through directed paths. Note that this homotopy is invertible. I believe that it should be possible to define the standard retractions of an -simplex onto a horn such that given a directed path the map
is increasing for all . Then if we define the simplicial set it should be a quasicategory with a map to Urs’ fundamental quasicategory.
-
- CommentRowNumber85.
- CommentAuthorTim_Porter
- CommentTimeOct 6th 2010
To a large extent I agree with you, Urs. You say
And that looking at this glaring open problem does adjust some intuitions about what directed spaces should obviously be like
I think I would say ’And that looking at this glaring open problem does add some knowledge about what directed spaces are like.’
If one identified a class of directed spaces that did correspond to quasi-categories, that would provide us with very useful insights/information and probably very useful methods, to attack at least some of the other types of ’directed spaces’ that seem to occur in examples. The classification of different classes of directed homotopy theories might be the aim. The interactions between them may be very enlightening.
I changed ’intuition’ to ’knowledge’, because the intuition is coming from a wide range of directions (some of which I intend to discuss in some new entries) and the applications are important. The open problem you mention would at very least provide newish examples of directed spaces which have a good directed homotopy theory but would also delimit and characterise that part of directed homotopy theory which can be faithfully modelled using quasicategories. I deleted ’obviously’ because although I have worked on directed homotopy theory quite a lot, I do not know exactly the ’correct’ form of input ’space plus ??? ’ that should be used in order to cover the desired examples in the best way.
-
- CommentRowNumber86.
- CommentAuthorMike Shulman
- CommentTimeOct 6th 2010
What I want is to highlight that there is a glaring open problem in directed homotopy theory (by whatever interpretation of the term): find the notion of directed space that proves a directed homotopy hypothesis with quasi-categories on one side.
I agree with that.
And that looking at this glaring open problem does adjust some intuitions about what directed spaces should obviously be like.
I don’t so much agree with that, because as I’ve said I think there are likely to be multiple useful notions of “directed space.” So finding out something about the ones which model quasicategories doesn’t mean that our prior intuitions about a different notion of directed space were wrong.
But yes, let’s not fight about terminology.
-
- CommentRowNumber87.
- CommentAuthorTim_Porter
- CommentTimeNov 21st 2010
- (edited Nov 21st 2010)
I have been tidying up directed topological space. I got rid of some of the older query boxes, and added in a bit more comment early on.
-
- CommentRowNumber88.
- CommentAuthorTim_Porter
- CommentTimeNov 21st 2010
Further I have added in a pair of examples from Marco’s book which illustrate the problem of finding small invariants of directed homotopy type.
1 to 88 of 88