Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory internal-categories k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

Atrium > Mathematics, Physics & Philosophy: Category that is not free?

Bottom of Page

1 to 32 of 32

  1.  
    • CommentRowNumber1.
    • CommentAuthorEric
    • CommentTimeMar 2nd 2010
    • (edited Mar 2nd 2010)

    Can someone give me a simple example of a category that is not the quiver of some directed graph?

    • CommentRowNumber2.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 2nd 2010

    A monoid, considered as a category with one object, or even a group.

    • CommentRowNumber3.
    • CommentAuthorEric
    • CommentTimeMar 2nd 2010

    Wow. Thanks for the speedy response :)

    Would you mind helping me understand that? Why isn't a monoid the quiver of a directed graph? I am envisioning a picture of a directed graph with one vertex and directed edges sprouting from it...

    • CommentRowNumber4.
    • CommentAuthorUrs
    • CommentTimeMar 2nd 2010

    In a free category on a graph morphisms are just words formed from the letters that are the graph edges. Composition does nothing but to concatenate such words. Nothing ever happens.

    For a list of examples of non-free categories, see also our collection of entries on categories.

    • CommentRowNumber5.
    • CommentAuthorEric
    • CommentTimeMar 2nd 2010
    • (edited Mar 2nd 2010)

    I'm probably thinking about it the wrong way, but if free categories are interpreted as images of applying the left adjoint 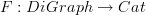F:DiGraph\to Cat of the forgetful functor 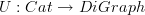U:Cat\to DiGraph, wouldn't they carry more information than "just words"?

    • CommentRowNumber6.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 2nd 2010

    I should correct this to be: a monoid/group that is not free. ACtually a group is a monoid that is not free so that any group should be sufficient.

    • CommentRowNumber7.
    • CommentAuthorUrs
    • CommentTimeMar 2nd 2010

    wouldn't they carry more information than "just words"?

    Nope, that's precisely the information they carry. That's what the word "free" means: forming the free category adds a notion of composition to the graph, but "freely" so, in that the resulting composition carries not a single bit of information.

    Try to think about this little exercise: now that you know how both functors F and U work, demonstrate the equation that characterizes the adjunction:

    Hom_{DiGraph}(G, U(C)) \simeq Hom_{Cat}(F(G),C)

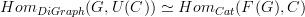
    Try it. It is easy and likely illuminating.

    • CommentRowNumber8.
    • CommentAuthorEric
    • CommentTimeMar 2nd 2010

    I will try if you tell me what "demonstrate the equation that characterizes the adjunction" means :)

    Would it be something like showing 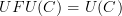UFU(C) = U(C) and FUF(G) = F(G)?

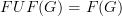    • CommentRowNumber9.
    • CommentAuthorTodd_Trimble
    • CommentTimeMar 2nd 2010

    Well, something like that. I imagine Urs means this: write out the explicit recipe for producing an functor 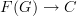F(G) \to C given an graph morphism 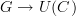G \to U(C), and also the recipe for going back the other way, and verify that these two recipes are indeed mutually inverse.

    Possibly it would be psychologically easier to work this out for the free-forgetful adjunction between monoids and sets. If that is comfortable, then rest assured that the mechanics in the present case are much the same.

    • CommentRowNumber10.
    • CommentAuthorEric
    • CommentTimeMar 2nd 2010

    Thanks! As promised, I will try, but it will have to wait. Busy busy!

    • CommentRowNumber11.
    • CommentAuthorTim_Porter
    • CommentTimeMar 2nd 2010

    @ Eric: have a glance at some group or monoid presentation stuff. If one has one generator, a and the relation that a^2 = 1, then the monoid cannot be free on anything. Just see if you can satisfy the free category category condition on any of the (large number :-)) of possibilities. The identity must be sent to something and the single other element must as well. Now play!

    • CommentRowNumber12.
    • CommentAuthorEric
    • CommentTimeMar 2nd 2010

    Thanks Tim! I got a sense of deja vu when you wrote that. I'm sure I've had this conversation before, but I'm getting old and my brain wasn't too good to start with :)

    Isn't 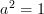a^2 = 1 "evil"? Is there a "non evil" group that is not free?

    • CommentRowNumber13.
    • CommentAuthorUrs
    • CommentTimeMar 2nd 2010

    Isn't 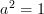a^2 = 1 "evil"?

    No, because this is about morphisms, not objects. Equations between objects are evil and want to be isomorphisms instead. But equations on morphisms in a category are fine.

    • CommentRowNumber14.
    • CommentAuthorTim_Porter
    • CommentTimeMar 2nd 2010

    Aha! Of course, a 2=1a^2 = 1, is not ’true’, but it is not truly ’evil” either. The point is that a 2a^2 is in level 1 of the corresponding 2-category. If you like that sort of picture, look at the projective plane, where you see the 2-cell explicitly. If you go twice around the disc, you get back where you started (up to homotopy). (Question: is that the same place or not? What does ’the same’ mean? etc.) But take a playing card, place it on the table, turn it over, turn it over again. Are you back where you started or not? It depends!!!!! (I get confused, as it does just seem to depend on what you are trying to do.)

    What your question seems to ask is : is there a group with a presentation which is without relations, and which is not free? and of course, then the answer will be NO.

    • CommentRowNumber15.
    • CommentAuthorUrs
    • CommentTimeMar 2nd 2010

    @Tim: you need double dollar signs here on the forum to get math displayed pretty-printed

    @Eric: as Tim indicates, there is a story to be told for what happens when we don't work with categories and identify morphisms, but work with oo-categories and just talk about equivalences between morphisms. But I don't think it is wise to get into this before feeling at home with concepts like a free category.

    The problem of evil is not something that you should worry about right now! :-)

    • CommentRowNumber16.
    • CommentAuthorEric
    • CommentTimeMar 2nd 2010
    • (edited Mar 2nd 2010)

    Equations between objects are evil and want to be isomorphisms instead. But equations on morphisms in a category are fine.

    But in an arrow category, the arrows are objects so what is evil in one category may not be evil in another :) Who gets to decide what is evil and what is not? It seems prejudiced :)

    I imagine Urs means this: write out the explicit recipe for producing an functor F(G) \to C given an graph morphism G \to U(C), and also the recipe for going back the other way, and verify that these two recipes are indeed mutually inverse.

    Given a graph G, we get a category PG whose objects are the nodes of G and whose morphisms are the paths in G. Composition of morphisms is composition of paths. But I'm a little hesitant about identifying PG with F(G). F is a functor

    F:DiGraph\to Cat

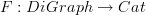
    so the image F(G) depends on the nature of F. For instance, we could have

    G\mapsto Vect,

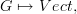
    in which case F takes nodes of G to a vector spaces in Vect. This is what I meant when I said I thought the free category was more than just words. I would describe PG as "just words" but F(G) depends on the nature of F.

    I might need a little more prodding to get me to understand what it means to "demonstrate the equation that characterizes the adjunction". Could someone help me parse it a little more?

    I know how to get PG starting from G, but as you can see, I'm hesitant to identify this with F(G), so I'm a little stuck.

    I have an idea about

    U:Cat\to DiGraph

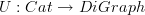
    but it is probably not correct. I am tempted to say that we want to "forget" all morphisms of any C in Cat that are composites of other morphisms. The resulting directed graph would consist of "primordial" morphisms, i.e. those that are not composites of others, i.e. elementary. I like this, but I can imagine bumping into difficulties when dealing with smoothness (another reason not to like smoothness) :)

    Is there any hope for me to get back on track? :)

    • CommentRowNumber17.
    • CommentAuthorEric
    • CommentTimeMar 2nd 2010

    If you go twice around the disc, you get back where you started (up to homotopy). (Question: is that the same place or not? What does ‘the same’ mean? etc.)

    I have an unorthodox way to think about this stuff, because I live in a causal universe and I think categories are nicely suited for describing causal stuff. For instance, I think of a category as having something of a built-in measure of time. For a physical system where we have

    a^2 = 1,

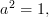
    then the "1" here is not really the identity because it took at least two ticks of clock to get there. So I would say we could label the morphism "a" with time stamps, e.g. a(0,1), which means if we apply "a" at time "0" we get a result at time "1". Then

    a^2 = 1

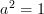
    becomes rather

    a(1,2)\circ a(0,1) = 1(0,2)

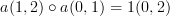
    where 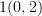1(0,2) means "just sits there for two time steps". In other words, if we apply "a" at time "1" and "a" again at time "2" it is the same thing as sitting still for two time steps.

    Another way to say it is that I like to "extrude categories in time". In this way, even groups with elements 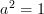a^2 = 1 are free when we properly interpret each action, i.e. morphism, as requiring some time to perform.

    • CommentRowNumber18.
    • CommentAuthorUrs
    • CommentTimeMar 2nd 2010
    • (edited Mar 2nd 2010)

    But in an arrow category, the arrows are objects

    This is an evil thing to say!

    You are identifying objects in a category with some other thing you have in mind. This may be the way you present a category, but once you have the category, what its object are is a question entirely intrinsic to that category. What you think of an object as being has in general no intrinsic reality.

    so the image F(G) depends on the nature of F

    But we have already fixed F as being the left adjoint to the forgetful functor.

    For instance, we could have G\mapsto Vect ,

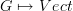    No, why? F maps G to the free category over it. Not to Vect.

    • CommentRowNumber19.
    • CommentAuthorTim_Porter
    • CommentTimeMar 2nd 2010
    That was one of the senses in which I said 'it depends'!
    • CommentRowNumber20.
    • CommentAuthorUrs
    • CommentTimeMar 2nd 2010
    • (edited Mar 2nd 2010)

    I might need a little more prodding to get me to understand what it means to "demonstrate the equation that characterizes the adjunction".

    So as you said correctly in your frist sentence, the free category functor F takes a graph G to the category that you wrote PG, objects are the vertices of G, morphisms are words of fitting edges in G, composition of morphisms is concatenation of words.

    Now demonstrate that this F really is the left adjoint functor to the forgetful functor from categories to graphs:

    you need to show that given any graph G and any category C, there is a bijection between the set of functors of the form

    F(G) \to C

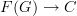
    and the set of graph morphisms of the form

    G \to U(C) .

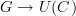    Here maybe the first one you prefer to write as P G \to C .

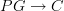    Say precisely what this bijection is: given a functor 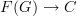F (G) \to C, which graph morphism 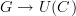G \to U(C) do you send it to? And how do you go the other way round?

    And eventually you should show that the bijection is natural in G and C. But wait with this until the bijection itself is clear.

    • CommentRowNumber21.
    • CommentAuthorMike Shulman
    • CommentTimeMar 2nd 2010

    But in an arrow category, the arrows are objects so what is evil in one category may not be evil in another

    Saying that two arrows f:A-->B and g:C-->D are equal as objects of the arrow category actually involves three assertions: that the object A equals the object C, that the object B equals the object D, and finally that as parallel arrows, f and g are equal. Of these, the first two are already evil in the original category, so there is no contradiction. Equality of arrows is only non-evil when the arrows in question are given to you as being parallel.

    • CommentRowNumber22.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 2nd 2010

    @Eric, to expand on what Mike said:

    Say we are working in foundations like SEAR where equality of arbitrary elements of different sets is not a meaningful question, and we have to be careful of 'evil'.

    Then for an internal category (aka a small category) equality of arbitrary arrows is meaningful, as (generally) a priori the internal category is given to you as a set of objects and a set of arrows, and so all the arrows are in the same set and can be compared for equality.

    For a large category, it only has a collection of objects, and for each pair of objects 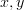x,y a hom-set 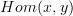Hom(x,y). An arbitrary pair of arrows belongs to an arbitrary pair of hom-sets, and so can't be compared in general. When forming the arrow category of this large category, the objects of the arrow category only form a collection, consisting of the elements of all the hom-sets of the original category, and this isn't a set (the collection isn't formed out of the hom-sets by the set-builder rules of our foundations).

    If, as Mike says, you know from the start that the arrow are parallel, then they are elements of the same hom-set, and so can be legitimately compared for equality.

    • CommentRowNumber23.
    • CommentAuthorEric
    • CommentTimeMar 3rd 2010
    • (edited Mar 3rd 2010)
    This comment is invalid XML; displaying source. <blockquote> <blockquote> <p>For instance, we could have <img src="/extensions/vLaTeX/cache/latex_fac139fd4e6b9ee72d6600f87e42b09e.png" title="G\mapsto Vect" style="vertical-align:-20%;" class="tex" alt="G\mapsto Vect" /> ,</p> </blockquote> <p>No, why? F maps G to the free category over it. Not to Vect.</p> </blockquote> <p>Sorry. I'm obviously confused. When we write</p> <img src="/extensions/vLaTeX/cache/latex_07a88eb6f108bb5de72158f07c10520a.png" title="U:Cat\to DiGraph" style="vertical-align:-20%;" class="tex" alt="U:Cat\to DiGraph" /> <p>I thought U sends any object of Cat to a directed graph. Since Vect is an object in Cat, I thought we'd have</p> <img src="/extensions/vLaTeX/cache/latex_27bb1c7581e1436cbcb07ac173974aa3.png" title="Vect\mapsto G" style="vertical-align:-20%;" class="tex" alt="Vect\mapsto G" /> <p>for some G. If that is the case, I thought the adjoint would go the other way and we could have</p> <img src="/extensions/vLaTeX/cache/latex_b9320030ad32f3a137b0538f0cdd6072.png" title="G\mapsto Vect." style="vertical-align:-20%;" class="tex" alt="G\mapsto Vect." /> <p>I suppose what you are saying is that F maps <i>only</i> to path categories? That wouldn't be very fun :)</p> <p>Maybe I need a new name for what I had in mind. For finite categories, I think I understand how it works. Take, for example, a category with three objects a,b,c and three morphisms:</p> <p><img src="/extensions/vLaTeX/cache/latex_6eb6590620777feea4b20dd75d58ac39.png" title="f:a\to b" style="vertical-align:-20%;" class="tex" alt="f:a\to b" /><br></p> <p><img src="/extensions/vLaTeX/cache/latex_2d587dd1b6850077b0995d3040681548.png" title="g:b\to c" style="vertical-align:-20%;" class="tex" alt="g:b\to c" /><br></p> <p><img src="/extensions/vLaTeX/cache/latex_8859945d294e385e4df2f6c56594dbee.png" title="gf:a\to c." style="vertical-align:-20%;" class="tex" alt="gf:a\to c." /><br></p> <p>If I call this category C, then I thought the forgetful functor</p> <img src="/extensions/vLaTeX/cache/latex_07a88eb6f108bb5de72158f07c10520a.png" title="U:Cat\to DiGraph" style="vertical-align:-20%;" class="tex" alt="U:Cat\to DiGraph" /> <p>applied to C would give the directed graph G with three nodes a,b,c and two directed edges ab and bc. Is that right?</p> <p>Then I thought we can completely recover C by forming the free category F(G).</p> <p>Then I started wondering if any (finite? countable?) category can be recovered this way from its underlying "elementary graph". Hence this thread.</p>
    • CommentRowNumber24.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 3rd 2010
    • (edited Mar 3rd 2010)

    The directed graph 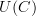U(C) has six edges: one for each of the identity arrows, and one for each of 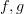f,g and their composite.

    I suppose what you are saying is that F maps only to path categories? That wouldn't be very fun :)

    pretty much. Given a directed graph, the free category on it has as arrows the paths of finite length, and composition is concatenation. No arrows are invertible, and only identities are additionally required to exist, associativity being automatic.

    • CommentRowNumber25.
    • CommentAuthorEric
    • CommentTimeMar 3rd 2010

    Thanks David. As is often the case, the picture in my head is not translating into the proper words. If U(C) has six edges, it definitely isn't what I'm thinking about.

    In the other direction, I'm thinking of some kind of functor from DiGraph to Cat where each directed edge maps to a morphism, but in a way that carries more information than "just words". For example,

    G\mapsto Set.

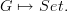
    Here, I want directed edges in G mapping to functions in Set. Maybe I'm thinking about something related to category of elements.

    • CommentRowNumber26.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 3rd 2010

    For that to happen, one needs to pick a set for each vertex first. You could pick every such set to have one element, but then the resulting image of 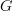G inside 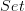Set is contractible.

    • CommentRowNumber27.
    • CommentAuthorHarry Gindi
    • CommentTimeMar 3rd 2010

    @Eric: I have some really good notes and exercises that my professor typed up for a seminar at chicago as a supplement to HTT ch. 1 and appendices I & II, which seem like they might be useful to you. I don't think he'd be happy with putting them up on the nLab (although I can ask), since he thinks that they aren't really polished enough, but if you'd like me to email them to you, they discuss this question in detail and seem like they might be of interest to you.

    • CommentRowNumber28.
    • CommentAuthorEric
    • CommentTimeMar 3rd 2010
    • (edited Mar 3rd 2010)

    Thanks Harry. I'd really appreciate that.

    • CommentRowNumber29.
    • CommentAuthorHarry Gindi
    • CommentTimeMar 3rd 2010

    It's sent.

    • CommentRowNumber30.
    • CommentAuthorUrs
    • CommentTimeMar 3rd 2010

    I thought the adjoint would go the other way

    Yes, the adjoint functor goes the other way -- but is not the inverse functor. If U sends Vect to G, then G need not be sent back to Vect by F. That's what an inverse functor would do.

    But there is no inverse to U. The F is in some way the "best approximation from the left" to that missing inverse.

    • CommentRowNumber31.
    • CommentAuthorAndrew Stacey
    • CommentTimeMar 3rd 2010

    @Harry:

    I don't think he'd be happy with putting them up on the nLab (although I can ask), since he thinks that they aren't really polished enough,

    That's one of the reasons of existence of the nlab! Polishing!

    • CommentRowNumber32.
    • CommentAuthorHarry Gindi
    • CommentTimeMar 3rd 2010

    @Andrew: It's not my place to put them up, since he asked me not to distribute them when he sent them to me.

1 to 32 of 32

  1.