nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeMar 12th 2010
- (edited Mar 12th 2010)
expanded (infinity,1)-category of (infinity,1)-functors : more details, more statements, more proofs. In particular concerning the model by the global model structure on functors.
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeMar 15th 2010
added remakrs and pointers from global model structure on functors to (infinity,1)-category of (infinity,1)-functors.
What I still don't fully know is the general statement what invariant notion precisely the Reedy model structures model.
-
- CommentRowNumber3.
- CommentAuthorMike Shulman
- CommentTimeMar 15th 2010
Since the weak equivalences in the Reedy model structure are the same as those in the projective and injective model structures, it should model the same
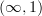 -category, no?
-category, no? -
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeMar 15th 2010
Right. But the Reedy model structure exists without assumptions on the codomain. What if the codomain is not combinatorial, for instance? Does the Reedy model structure still present the (oo,1)-functor (oo,1)-category?
In any case, I see that some polishing of the discussion of the relation to the proj/in j-structure at Reedy model structure was in order: created section Properties.
-
- CommentRowNumber5.
- CommentAuthorMike Shulman
- CommentTimeMar 16th 2010
Good question. I would be surprised if the answer were no, but I don't actually know. Note that the projective model structure requires the codomain only to be cofibrantly generated. There do, of course, exist model categories that aren't cofibrantly generated.
1 to 5 of 5