Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology definitions deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nforum nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: Reedy categories

Bottom of Page

1 to 21 of 21

  1.  
    • CommentRowNumber1.
    • CommentAuthorMike Shulman
    • CommentTimeMar 13th 2010

    Created direct category and generalized Reedy category (well, un-stubbified the latter) as spinoffs from Reedy category.

    • CommentRowNumber2.
    • CommentAuthorEric
    • CommentTimeMar 13th 2010
    • (edited Jul 7th 2010)

    Is there a name for a process I outlined on the nCafe a while back, where we take a category and "extrude" it into something like "discrete time"?

    For example, consider a category with two objects a,b and two non-identity morphisms

    f:a\to b g:b\to a

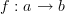
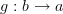
    Now I want to "form a cylinder" of this category (please read this losely as I'm most likely not using the terms correctly) or "extrude it in time". To do this, we create a bunch of copies of a and a bunch of copies of b and label then with integers.

    We also make a bunch of copies of the morphisms and label them with two integers.

    The key is that now the morphisms cause the index to change, i.e.

    f(i,j): a(i)\to b(j).

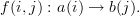
    A consequence of this is that we have non-identity identity-like morphisms

    id(i,j): a(i)\to a(j).

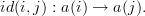
    The true identity morphisms are the ones with the same integer in both labels, e.g.

    id(i,i): a(i)\to a(i).

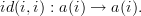
    I'm pretty sure this procedure can always be done for groupoids and I can't see anything keeping us from doing it for a general category either. In fact, I sometimes try to use this trick to "unwrap" a groupoid into a category by insisting that each morphism increases the index by 1 so that

    f^{-1}(i+1,i+2)\circ f(i,i+1) = id(i,i+2).

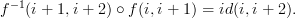
    When I read the entries Mike just created, it resonated with the way I think about the stuff above. Especially when I saw that any groupoid is a generalized Reedy category. How does that work, by the way?

    Can any category be "extruded" like this into a (generalized?) Reedy category?

    • CommentRowNumber3.
    • CommentAuthorMike Shulman
    • CommentTimeMar 13th 2010

    Ignoring Eric's question for the moment (-: I also edited geometric shapes for higher structures to refer to these notions. I also removed Ronnie Brown's comment, which it looked to me like was originally just an example making the argument that cubical methods are important, rather than something intended to remain on the page -- it wasn't really appropriate on a page discussing all the different sorts of shapes quite generally.

    • CommentRowNumber4.
    • CommentAuthorMike Shulman
    • CommentTimeMar 13th 2010

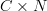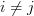    Eric: Yes, I think so. If C is any category, consider the product category C\times N ,where N is the poset of natural numbers with the usual ordering, and then take the subcategory consisting of those pairs (f, i\le j) such that either (1) f is an isomorphism or (2) i\neq j. This is a generalized direct category. If instead of "f is an isomorphism" we say "f is an identity" then we get a non-generalized direct category. We could also replace N by any ordinal.

    Re: groupoids being generalized Reedy categories, just check the definition! Every object can have degree 0.

    • CommentRowNumber5.
    • CommentAuthorEric
    • CommentTimeMar 14th 2010

    Thanks Mike :)

    I think what you described is close to what I had in mind, but in that setup would it be possible to have a morphism

    f:a\to b

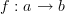
    "extruded" to multiple morphisms starting from the same labeled object? For example, could we have

    f(i,j):a(i)\to b(j)

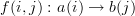
    and

    f(i,k):a(i)\to b(k)

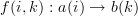
    for j\ne k?

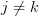    If so, then I might want to restrict things a little more. My motivation is to try to assign a time interval to each morphism so that mapping one object to another always takes some time. Allowing 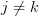j\ne k would mean we assign different time intervals to the same morphism.

    Is there a succinct way to find the "smallest" direct category that comes from extruding any (non-direct) category?

    • CommentRowNumber6.
    • CommentAuthorEric
    • CommentTimeMar 14th 2010

    Incidentally, I just happened to be glancing at Lawvere's Taking Categories Seriously (a beautiful paper!), where he discusses "direct systems".

    • CommentRowNumber7.
    • CommentAuthorMike Shulman
    • CommentTimeMar 14th 2010

    Yes, in the construction I described, each noninvertible f goes from a(i) to b(j) whenever 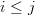i\le j. Perhaps what you want is an "N-graded category"? In general, if M is any monoid, then an M-graded category is a category in which every morphism is assigned an element of M, called its "degree," such that identities have degree 0 and 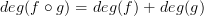deg(f\circ g) = deg(f) + deg(g). If C is an M-graded category, then you could define a category with object set 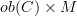ob(C)\times M and with a morphism from (a,m) to (b,n) being a morphism f from a to b in C such that m+deg(f)=n. If M is the natural numbers, then this category will be direct. But in general, for an arbitrary category C, there needn't be any nontrivial way to make it N-graded. For instance, in an M-graded category, any isomorphism must have a degree which is invertible in M, which when M=N means that it must be 0; thus no groupoid admits any nontrivial N-grading. Likewise, any idempotent in an N-graded category must have degree 0, and hence so must any split monic or split epic, so you can construct lots more categories admitting no nontrivial N-grading.

    • CommentRowNumber8.
    • CommentAuthorEric
    • CommentTimeMar 14th 2010
    • (edited Mar 14th 2010)

    Thanks Mike. M-graded categories seem like what I had in mind. I'd probably choose some rig for M.

    Regarding isomorphisms...

    I'm wondering if there is a process to take a category C and turn it into a direct graded category DC along similar lines as I've attempted above, i.e. extruding etc. This would hopefully be done in a way that the original category can be recovered by "projecting along the direction".

    In the case of groupoids, and any isomorphism for that matter, I don't expect inverses in C to be inverses in DC. All morphisms have a positive time interval associated with them, even inverses. How does that work? The best I can try to explain it is via the example I've mentioned a couple of times. Let

    f:a\to b

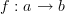
    be an isomorphism in C. In C we have

    f^{-1}\circ f = id.

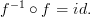
    However, in DC we would have

    f^{-1}(i+1,i+2)\circ f(i,i+1) = id(i,i+2).

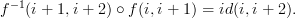
    Here id(i,i+2) is not an identity morphism in DC. In DC, id(i,i+2) means essentially "sit here without doing anything from time i to time i+2".

    In this way, groupoids pose no particular problem that I can see. Given any groupoid G, we should be able to obtain a direct graded category DG this way. Then we can recover G from DG by "forgetting the indices" or put another way "projecting along the direction".

    Note that a direct graded category DC obtained this way will never contain any inverses even if C is a groupoid.

    Edit: I'm on shaky ground when I start using the word "functor" and even more shaky ground if I dare utter "adjoint", but given a direct graded category DC, there is a forgetful functor

    U:DC\to C.

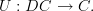
    So maybe this "extruding" stuff I'm talking about might be an adjoint to this forgetful functor, which makes me want to describe it as "Given a category C, let DC be the free direct graded category." Or something...

    • CommentRowNumber9.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 14th 2010
    If DC has no isomorphisms, there can't be a functor from C to DC that doesn't take all the isomorphisms in C to identities. But the other description, namely

    >"Given a category C, let DC be the free direct graded category."

    is better. This sounds like a candidate for a functor Cat -> DirectCat, adjoint to the inclusion DirectCat -> Cat
    • CommentRowNumber10.
    • CommentAuthorEric
    • CommentTimeMar 15th 2010

    If DC has no isomorphisms, there can't be a functor from C to DC that doesn't take all the isomorphisms in C to identities.

    Oh right. Thanks David. For my own benefit (and maybe a young student somewhere), I'll spell it out:

    With the map

    F: C\to DC

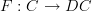
    I outlined, it is not a functor because

    F(f^{-1})\circ F(f) \ne id_{F(a)}.

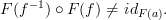
    But it is "close". So maybe there is another word besides "functor" that can save the day? :)

    If I knew how to construct adjoints, I'd give the second prescription a try. I will give it a try, but have low expectations :)

    By the way, is the word "graded" important here? Maybe I should try to construct the adjoint of a forgetful functor

    U:DirectGCat\to Cat.
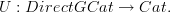
    • CommentRowNumber11.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 15th 2010
    This comment is invalid XHTML+MathML+SVG; displaying source. <div> <blockquote> <p>Maybe I should try to construct the adjoint of a forgetful functor <img src="/extensions/vLaTeX/cache/latex_c3071ff632b5dbb07120d4e9311cfebb.png" title="U:DirectGCat\to Cat." style="vertical-align: -20%;" class="tex" alt="U:DirectGCat\to Cat."/></p> </blockquote> <p>Yep - this is what I would do. But first construct a functor, then check if it is an adjoint, because just the functor can be useful.</p> <p>As for</p> <blockquote> <img src="/extensions/vLaTeX/cache/latex_888964d98f2f2f07512a76e931ee76fe.png" title="F(f^{-1})\circ F(f) \ne id_{F(a)}." style="vertical-align: -20%;" class="tex" alt="F(f^{-1})\circ F(f) \ne id_{F(a)}."/> </blockquote> <p>you can use a simpler condition, namely that we have to have <img src="/extensions/vLaTeX/cache/latex_ec08cb5302f0ca99209e3bd1d0dcd17e.png" title="F(f^{-1}) = F(f)^{-1}" style="vertical-align: -20%;" class="tex" alt="F(f^{-1}) = F(f)^{-1}"/>, and the latter doesn't exist unless <img src="/extensions/vLaTeX/cache/latex_174a121b8de9558ce185a02fa36b6697.png" title="F(f) = id_{something}" style="vertical-align: -20%;" class="tex" alt="F(f) = id_{something}"/> as there are no nontrivial isomorphisms.</p> </div>
    • CommentRowNumber12.
    • CommentAuthorEric
    • CommentTimeMar 15th 2010

    Sounds good. I will try (time allowing):

    Free Direct Graded Categories (ericforgy)

    • CommentRowNumber13.
    • CommentAuthorMike Shulman
    • CommentTimeMar 15th 2010

    This may not be a problem for what you're looking for (I don't really know what you're looking for), but I observe that the condition

    f^{-1}(i+1,i+2) \circ f(i, i+1) = id (i, i+2)

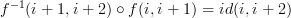
    violates the condition you asked for above, that every morphism be assigned a unique time interval. Namely, here the identity 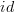id has both the time interval 0 (giving the actual identity in DC) and the time interval 2 (so that the above composite is possible). Perhaps you only wanted nonidentity morphisms to have unique time intervals? But if identities can have a nonzero time interval k, then any morphism with time interval i must also have time interval i+k, i+2k, i+3k, etc., since we can compose it with an identity on either side.

    • CommentRowNumber14.
    • CommentAuthorEric
    • CommentTimeMar 15th 2010

    It is admittedly a HORRIBLE notation and I should change it, but when I wrote (thinking as a physicist)

    id(i,i+2)

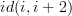
    this means "sit here for 2 steps and do nothing". This would be an identity in C (where there is no time), which I view as "space", but it is not an identity in DC, which I view as "spacetime". The only identities in DC are of the form id(i,i).

    One picture I am relying on is that id(i,i+t) can be thought of as tracing out a "geodesic" (or the path of a particle at rest) in C and t is like "proper time".

    • CommentRowNumber15.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 15th 2010
    So really id(i,i+2) is like (id,(i,i+2)) in C x N...
    • CommentRowNumber16.
    • CommentAuthorEric
    • CommentTimeMar 15th 2010

    So really id(i,i+2) is like (id,(i,i+2)) in C x N...

    Yes yes :) That is the better way to write it I suppose. Thanks.

    When you write N, I suppose you mean the "preorder of natural numbers". But I can think of a couple different ways to make a preorder out of natural numbers, e.g. one with morphisms going in just one direction (so like a rig?) and another with arrows going in both directions. If the former, then I think C x N is what I've been calling a direct graded category.

    Maybe a better name is simply N-graded category, where N is the rig of natural numbers, which is also a direct category. Would there be any other categories that are both graded and direct other than this one? If not, then maybe I will stick with "direct graded category".

    • CommentRowNumber17.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 15th 2010
    I don't know how to think about N with arrows in both directions - I certainly mean the usual preorder with objects N. A preorder with arrows going in both directions would likely be contractible (equivalent to the trivial category), if I get your drift. I'm not sure how a grading on C x N interacts with the usual order on N and compared to an N-grading on C.

    I think I get what you mean with the 'extrusion'. If you don't mind the fact everything can be done in unit time, then C x N is fine, but if you want to specify that different things take different minimum times to do, then things get a bit tricky.

    Maybe consider this example: the category M(X) where object are the points of a Riemannian manifold X, and arrows are (piecewise) smooth paths [0,a] -> X, where a is non-negative (M for Moore paths). Then there is a functor length:M(X) -> B[0,oo) where B[0,oo) is the one-object category associated to the monoid [0,oo) with addition. By looking at the subcategory M_N(X) of paths of non-negative integral length, we get a functor M_N(X) -> BN, where BN is the category associated to N as a monoid with addition. Thinking up some geometric examples (we can relax the requirement that things are smooth, they just need to be integrable) of shapes, which are then extruded in interesting ways, I leave to you :)

    NB: I hesitate to extend this to paths of all integral length, as then we would have to pass to the groupoid BZ as codomain, but the notion of the length functor will no longer make sense as we would have to have cancellation, which isn't possible.
    • CommentRowNumber18.
    • CommentAuthorEric
    • CommentTimeMar 15th 2010
    • (edited Mar 15th 2010)

    I don't know how to think about N with arrows in both directions

    Good. Neither do I, so we'll stick with the usual :) (I'm not fluent enough to know what is usual and what is not)

    If you don't mind the fact everything can be done in unit time, then C x N is fine

    I'm not sure if C x N is quite fine enough (if it is what I think it is), which is why I liked N-graded categories, which are also direct categories. If we take C x N, then I think we'd have both

    (f,(i,j)): (a,i)\to (b,j)

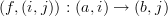
    and

    (f,(i,k)): (a,i)\to (b,k)

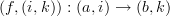
    for 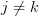j\ne k, which is something I don't want to have because this would be assigning multiple time intervals to the same morphism in C. Therefore, assigning a single natural number to each morphism seems closer.

    The object set of DC should be obj(C) x N.

    For each morphism

    f:a\to b

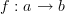
    in C, we'd have an infinite set of morphisms in DC

    mor(DC) = \{(f,(i,i+n)) | f\in mor(C), i\in obj(N)\}

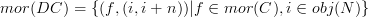
    each labeled with both an index 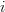i indicating the source object and an index n indicating the time interval, which is the same for all i.

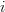    Still not sure about the best notation. 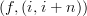(f,(i,i+n)) is probably the best we can do, but this is some kind of subcategory of C x N (ouch! as I recall Tom's recent article)...

    • CommentRowNumber19.
    • CommentAuthorEric
    • CommentTimeMar 15th 2010
    • (edited Jul 7th 2010)

    I think I finally understood Mike's comment above. Sorry for being slow. That is a good observation.

    Hmmm....

    • CommentRowNumber20.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 15th 2010

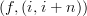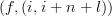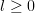    Given any (f,(i,i+n)), you may have (f,(i,i+n+l)) for l \geq 0 i.e. do something, and then do nothing for a while. This is not quite the same as waiting for a bit, then doing something, but this is just heuristics. Some small worked examples would be helpful, say at the page you set up.

    • CommentRowNumber21.
    • CommentAuthorEric
    • CommentTimeMar 15th 2010

    Thanks for your patience :)

    I will have a go at this (as time allows) and report back if/when I make any progress. You've helped point me in the right direction for sure.

1 to 21 of 21

  1.